
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Какой вид имеет линейное реккурентное уравнение n-го порядка
Пусть заданы числа 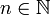 и
и 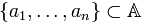 . Уравнение
. Уравнение

называется линейным однородным разностным (или возвратным) уравнением 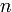 -го порядка (над множеством
-го порядка (над множеством 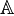 ). Пусть числа
). Пусть числа 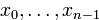 заданы. Тогда уравнение определяет линейную рекуррентную1)(или возвратную) последовательность
заданы. Тогда уравнение определяет линейную рекуррентную1)(или возвратную) последовательность 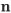 -го порядка: начиная с
-го порядка: начиная с  , каждый элемент
, каждый элемент  этой последовательности определяется через
этой последовательности определяется через 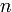 предшествующих.
предшествующих.
Пример. Уравнение первого порядка 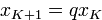 определяет — при задании
определяет — при задании 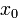 — геометрическую прогрессию.
— геометрическую прогрессию.
Пример. Уравнение второго порядка
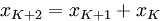
определяет при 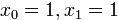 последовательность чисел Фибоначчи — они обозначаются буквой
последовательность чисел Фибоначчи — они обозначаются буквой 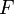
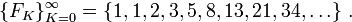
42.Что такое общее и частное решения линейного однородного реккурентного уравнения 2-го порядка?


43. Какой вид имеет общее решение линейного однородного реккурентного уравнения в случае различных характеристических корней?
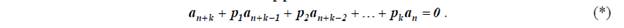
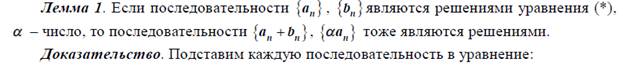



44. Какой вид имеет общее решение линейного однородного реккурентного уравнения 2-го порядка в случае одинаковых характеристических корней?

45. В каких случаях и каким образом можно найти частное решение линейного неоднородного реккурентного уравнения (по виду правой части)?
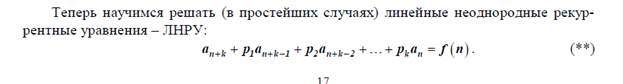


46. Что вы знаете о числах Фибоначчи?
Чи́сла Фибона́ччи — элементы числовой последовательности
в которой каждое последующее число равно сумме двух предыдущих чисел. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)[1]. Иногда число 0 не рассматривается как член последовательности.
Более формально, последовательность чисел Фибоначчи 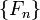 задается линейным рекуррентным соотношением:
задается линейным рекуррентным соотношением:
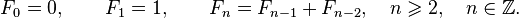
На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Liber Abaci» (1202). Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, предполагая что: изначально есть новорожденная пара кроликов (самец и самка), со второго месяца после своего рождения кролики начинают спариваться и каждый месяц производить новую пару кроликов, кролики никогда не умирают. Сколько пар кроликов будет через год?
· В начале первого месяца есть только одна новорожденная пара (1).
· В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1)
· В конце второго месяца первая пара рождает новую пару и опять спаривается (2)
· В конце третьего месяца первая пара рождает еще одну новую пару и спаривается, вторая пара только спаривается (3)
· В конце четвертого месяца первая пара рождает еще одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5)
В конце  -го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количество новорожденных пар, которых будет столько же, сколько пар было два месяца назад. Таким образом:
-го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количество новорожденных пар, которых будет столько же, сколько пар было два месяца назад. Таким образом: 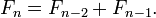
· Последовательность чисел Фибоначчи является частным случаем возвратной последовательности, её характеристический многочлен 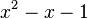 имеет корни
имеет корни 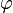 и
и 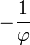 .
.
Дата добавления: 2015-01-19; просмотров: 212; Мы поможем в написании вашей работы!; Нарушение авторских прав |