
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
И вычтем из полученного выражения уменьшенные вдвое левую и правую части первого полученного нами уравнения. В результате получим
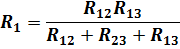
Аналогично и для других двух сопротивлений звезды

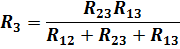
Таким образом, сопротивление луча эквивалентной звезды равно произведению сопротивлений двух сторон треугольника, которые присоединены к той же вершине, что и луч звезды, деленному на сумму сопротивлений, всех сторон треугольника.
Если сопротивления треугольника равны друг другу: R12 = R23=R13=RΔ, то будут равны друг другу и сопротивления звезды, т. е. R1 = R2=R3=R λ, причем получается простое соотношение
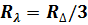
При обратном преобразовании звезды в эквивалентный треугольник, т. е. при заданных сопротивлениях R1, R2, R3, надо решить три уравнения относительно сопротивлений R12 ,R23 ,R13:
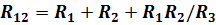
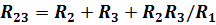
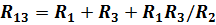
Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды.
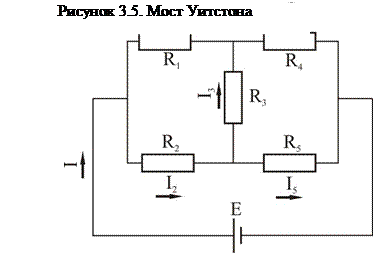 |
Мост Уитстона. Рассмотрим другой вид «сложного» соединения проводников - мостик Уитстона(рисунок 3.5)

Как явно видно из рисунка данную схему нельзя сразу же представить как суперпозицию параллельных и последовательных соединений. Так же нетрудно самому убедиться, что «честное» решение с записыванием множества уравнений для участков цепи и узлов тока, с последующим алгебраическим решением данной системы будет весьма утомительными. Поэтому для получения эквивалентного сопротивления для данной цепи воспользуемся полученной выше заменой треугольник-звезда. (рисунок 3.6)
Воспользуемся преобразованием звезда-треугольник для одного из треугольников (выделен на рисунке). Напомним, что полученные при преобразовании новые сопротивления R1,R2 и R3 связаны с сопротивлениями R12, R23 и R13 следующими соотношениями:
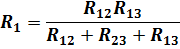

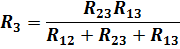
Дата добавления: 2015-01-19; просмотров: 330; Мы поможем в написании вашей работы!; Нарушение авторских прав |