
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ну а преобразованная цепь представляет собой набор последовательных и параллельных соединений. Получение ответа для эквивалентного сопротивления не вызывает никакого труда.

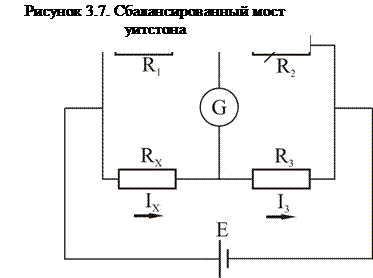
Но на практике как правило встречается более простой частный случай моста Уитстона- сбалансированный мост Уитстона. Сбалансированный мост( или уравновешенный мост) был предложен в 1833 Самуэлем Хантером Кристи, и в 1843 году усовершенствован Чарльзом Уитстоном как прибор для измерения электрического сопротивления. (рисунок 3.7)
Принцип измерения основан на взаимной компенсации сопротивлений двух звеньев, одно из которых включает измеряемое сопротивление. В качестве индикатора обычно используется чувствительный гальванометр, показания которого должны быть равны нулю в момент равновесия моста. Сопротивления R1,R2, и R3 в цепи известны, причем сопротивление R2 можно менять, добиваясь равновесия моста( нулевого тока через гальванометр). Давайте получим условие баланса моста. Запишем закон сложения токов для двух узлов:


Теперь рассчитаем потенциалы в двух замкнутых контурах:


Учитывая, что мост сбалансирован и IG=0, запишем систему уравнений:
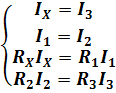
Решая систему уравнений получим:


Из полученной формулы для определения неизвестного сопротивления можно получить условие сбалансированности моста: Если выполняется соотношение RXR2=R1R3 (равны произведения диагональных сопротивлений), то ток через перемычку не течет. А значит перемычку можно представить как разрыв цепи и мост превращается в параллельное подключение двух пар последовательно соединенных резисторов.(рисунок 3.8)
А значит эквивалентное сопротивление цепи равно:

 |
Перерисовка схем. На практике часто встречаются задачи, когда цепи представлены в таком виде, что сразу и не понятно как к ним подступиться. И для решения задачи необходимо прежде всего перерисовать цепь в более привычный вид. Например рисунок 3.9.
Как видно из рисунка, левая схема является обычным мостом Уитстона. И если все сопротивления равны между собой R1=R2=R3=R4=R, то он сбалансирован, а значит ток через резистор R2 не пойдет, что совсем не очевидно по виду левого рисунка цепи.

Для того чтобы перерисовать схему нужно расставить точки равного потенциала. Напомним, что все точки одного проводника(соединяющего провода) имеют одинаковый потенциал. Более подробно рассмотрим еще один пример (рисунок 3.10)
Входную точку цепи обозначим точкой A, а выходную точкой D. Узел соединяющий резисторы R4,R2 и R3 назовем точкой B. Отметим, что потенциал точки В отличается от потенциалов точек А и D, так как двигаясь между ними по любому пути, всегда будет падать напряжение на одном из резисторов. Точка между резисторами R1 и R2 ,будет также иметь потенциал D, так как эта точка соединена с выходной точкой проводящем проводом.
Теперь начнем перерисовывать схему постепенно двигаясь от точки А к точке D. Из точки А в точку D можно попасть на прямую, через резистор R1. Двигаясь через резистор R4попадем в точку с потенциалом B. Из точки B можно попасть в точку D двигаясь как по резистору R2 так и по резистору R3, поэтому в перерисованной схеме они будут подключены параллельно.(Оба резистора имеют одну и ту же разность потенциалов jD-jB). В итоге перерисованная схема будет иметь вид как на рисунке 3.10 справа. Найти общее сопротивление получившейся схемы уже не составит никакого труда, так как это просто комбинация последовательных и параллельных соединений.
Примеры задач.
Задача 3.1

Определить токи в ветвях мостовой схемы (рисунок 3.11), если известны параметры цепи: E=4,4 В, R1=20 Ом, R2=60 Ом, R3= 120 Ом, R4=8 Ом, R5=44 Ом.
Решение. Заменив один из треугольников схемы, например ABC, образованный сопротивлениями R1, R2, R3, эквивалентной звездой, сопротивление лучей которой RA, RB, и RC, получим простую схему смешанного соединения элементов. Найдем сопротивления лучей звезды.



Эквивалентное сопротивление преобразованной цепи, состоящей из сопротивления RA и двух параллельных ветвей R4+RB и R5+RC

Ток в неразветвленной части схемы I=E/R=4,4/22 = 0,2 А. Ток в ветви с сопротивлениями R4 ,R5 находим но формулам «разброса» общего тока I


Для определения токов I1, I2, I3, которых нет в преобразованной схеме (рисунок 3.11), найдем потенциалы узлов C и B.
Напряжение на сопротивлении R4

Напряжение на сопротивлении R5
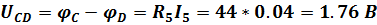
Полагая потенциал точки D равным нулю получаем:

Дата добавления: 2015-01-19; просмотров: 455; Мы поможем в написании вашей работы!; Нарушение авторских прав |