
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение I-й задачи динамики. Пример.
2)Теорема об изменении количества движения точки и система в дифф.и конечной формах.
1)Решение первой задачи.
 | 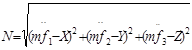 | ||
Пусть задан закон движения материальной точки в виде,
А так же её равнодействующая и масса m.
Из дифференциального уравнения движения материальной точки в
 |
декартовой системе координат следует, что:
 |  | ||
Аналогично решается первая задача для свободной точки, когда связи отсутствуют, а по известным уравнениям движения необходимо найти действующие на точку силы. В этом случае:
 |  | ||
 |
Пример.

Груз весом Р поднимается вертикально вверх по закону
Определить натяжение тросса.
 |  | ||
 Дано: Решение.
Дано: Решение.


 |
2)ТЕОРЕМА: Производная по времени от кинетического момента механической системы относительно неподвижного центра равен главному моменту всех внешних сил, действующих на систему относительно того же центра.
2)З-н сохранения количества движения:
Если геометрическая сумма всех внешних сил, приложенных к механической системе = 0, то её вектор количества движения постоянен. Воспользуемся дифф.формой теоремы об изменении количества движения механической системы.
.б) Если алгебраическая сумма проекций на какую либо ось всех действующих сил системы = 0, то проекция её вектора количества движения на эту ось есть величена постоянная.
6.1)Решение II-й задачи динамики. Постоянные интегрирования и их определения по начальным условиям. Пример.
2)Кинетический момент механической системы относительно центра и оси. Кинетический момент твёрдого тела вращающегося относительно оси.

1)Для решения этой задачи целесообразно воспользоваться дифф.ур-ми мат.точки в виде:

Поскольку действие силы известны, то => известны и правые части этих ур-й. Интегрирование их дважды по времени приводит их к 3-м ур-м содержащим 6 произвольным постонным:

Значе ния этих постоянных могут быть просто найдены с помощью нач.усл., т.е. если известно:

Подставив найденные значения в постоянные интегрирования в общее решение дифф-х ур-й получили закон движения точки:
Отсюда => , что мат.точка под действием одной и той же силы может совершать целый класс движений определённый начальными условиями.
 |  | ||
Например: движения свободной мат.точки под силами тяжести – семейств кривых 2-го порядка.
Начальные условия позволяют учесть влияние на движение мат.точки сил дейсвовавших на неё до того момента, который принят за начальный.
2)Закон сохранения кинетического момента механической системы:
1)Если сумма моментов относительно данного центра всех внешних сил = 0, то кинетический момент механической системы сохраняет модуль и направление в пространстве
2)Если сумма моментов всех действующих на систему внешних сил относительно некоторой оси = 0, то кинетический момент механической системы относительно этой оси есть величина постоянная.
Частные случаи:

Система вращается вокруг неподвижной оси в этом случае кинетический момент механической системы =
,и если сумма моментов относительно этой оси равна нулю, то

Дата добавления: 2015-01-19; просмотров: 215; Мы поможем в написании вашей работы!; Нарушение авторских прав |