
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Механическая система. Масса системы, Центр масс и его координаты.
2)Мощность. Работа и мощность сил, приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси.
1)Механической системой или системой материальных точек называется такая их совокупность, при которой изменение положения одной из точек вызывает изменение положения всех остальных. Примером механической системы может служить любая машина или механизм, где движение от одних частей машины или механизма передаётся с помощью связей другим частям. Твёрдое тело будем рассматривать как механическую систему, расстояния между точками которой неизменны. Системы, отвечающие этому условию называются неизменными. Системой свободных точек называется система материальных точек, движение которой не ограничивается никакими связями, а определяется только действующими на них силами. Пример- солнечная система. Системой несвободных точек называется система материальных точек, движения которых не ограничены связями. Пример- система блоков (полиспаст). Масса системы это сумма масс всех точек, входящих в систему. Центром масс механической системы называется точка радиус-вектор которой отвечает условию  , где
, где  - радиусы-векторы материальных точек
- радиусы-векторы материальных точек  . Спроектировав обе части этого равенства на оси OX, OY, OZ прямоугольной системы координат, получим выражение, определяющее координаты центра масс механической системы
. Спроектировав обе части этого равенства на оси OX, OY, OZ прямоугольной системы координат, получим выражение, определяющее координаты центра масс механической системы


 , где
, где  - координаты точек.
- координаты точек.
2)Предположим, что к твёрдому телу, вращающемуся вокруг неподвижной оси Z, приложены внешние силы  . Вычислим сначала элементарную работу отдельной силы
. Вычислим сначала элементарную работу отдельной силы  , которая приложена в точке
, которая приложена в точке 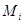 , описывающей окружность радиусом
, описывающей окружность радиусом  . Разложим эту силу на три составляющие, направленные по естественным осям траектории точки
. Разложим эту силу на три составляющие, направленные по естественным осям траектории точки 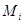
 . Определим момент силы
. Определим момент силы  относительно оси z как сумму моментов её составляющих относительно этой оси. В общем момент силы
относительно оси z как сумму моментов её составляющих относительно этой оси. В общем момент силы  относительно оси Z равен моменту силы
относительно оси Z равен моменту силы  , которая лежит в плоскости, перпендикулярной оси Z
, которая лежит в плоскости, перпендикулярной оси Z  . При элементарном перемещении тела его угол поворота φ получает приращение dφ, а дуговая координата точки
. При элементарном перемещении тела его угол поворота φ получает приращение dφ, а дуговая координата точки 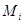 - приращение
- приращение  . Вычислим работу силы
. Вычислим работу силы  на этом перемещении как сумму работ трёх её составляющих. Работа сил
на этом перемещении как сумму работ трёх её составляющих. Работа сил  перпендикулярных вектору скорости точки
перпендикулярных вектору скорости точки 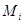 , равна 0, поэтому элементарная работа силы
, равна 0, поэтому элементарная работа силы 
 . Элементарная работа всех сил, приложенных к твёрдому телу
. Элементарная работа всех сил, приложенных к твёрдому телу  , где
, где  - Главный момент внешних сил относительно оси вращения z. Таким образом
- Главный момент внешних сил относительно оси вращения z. Таким образом  , т.е. элементарная работа сил, приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота. Мощность вычисляется по следующей формуле:
, т.е. элементарная работа сил, приложенных к твёрдому телу, вращающемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота. Мощность вычисляется по следующей формуле: 
Дата добавления: 2015-01-19; просмотров: 269; Мы поможем в написании вашей работы!; Нарушение авторских прав |