
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод цепей и сечений
Недостатком ТФН являются ее большие размеры. При расчете тестов на ЭВМ для хранения ТФН требуется большой объем памяти, что снижает размерность решаемых задач. В связи с этим для различных объектов диагноза разработаны специальные модели и методы, которые не имеют универсального характера, но с учетом особенностей объекта позволяют более просто решать задачи построения тестов.
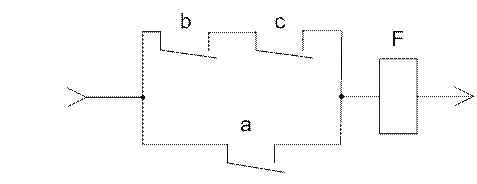
Рисунок 4 – Комбинационная релейно-контактная схема
Для релейно-контактных схем при построении проверяющих тестов используют метод цепей и сечений. Под цепью понимается набор состояний контактов, которые обеспечивают наличие цепей проводимости между полюсами схемы. Под сечением понимается набор состояний контактов, которые обеспечивают разрыв всех цепей схемы.
Перечисление всех цепей и сечений однозначно задает схему. Под цепью, урезанной на каком-то определенном контакте, понимают набор состояний контактов, соответствующий данной цепи, из которого исключен этот контакт. Аналогично определяют сечение, урезанное на каком-то определенном контакте.
В алгоритм вычисления проверяющей функции какого-то определенного контакта для неисправности типа «разрыв» (φº) выписывают все цепи, содержащие этот контакт и все сечения, содержащие этот контакт, определяют все сечения, урезанные на этом контакте. Каждую выписанную цепь рассматривают в сочетании с каждым урезанным сечением. Для них определяют входные наборы, на которых они одновременно существуют. Поверяющую функцию находят как объединение всех полученных наборов.
Алгоритм вычисления проверяющей функции для КЗ (φ¹) аналогичен алгоритму вычисления проверяющей функции для неисправности типа «разрыв», только термин цепь необходимо заменить на термин сечение.
Схема, представленная на рисунке 4, содержит 2 цепи: 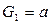 и
и 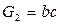 , а также 2 сечения:
, а также 2 сечения:  и
и 
· Для контакта «a» определим проверочную функцию φºа.
Контакт входит в цепь 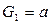 , а так же в сечение
, а так же в сечение  и
и 
Сечение урезанное на контакте а, равно 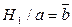 и
и 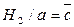
Цепь G1 существует при подаче входных переменных а1 = 1, а сечения H1/a – при b = 0 и H2/a – при с = 0, т.е. цепь G1, сечение H1/a и H2/a одновременно существуют на наборе  .
.
Таким образом 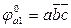
· Теперь для контакта «a» определим проверочную функцию φ¹a.
Контакт входит в сечения  и
и  , а так же в цепь
, а так же в цепь 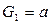 .
.
Цепь урезанная на контакте a, равна  .
.
Сечение H1 существует при значениях переменных а = 1, b = 1, H2 – при а=1, c=1, т.е. сечения Н1, H2 и цепь G1/a одновременно существуют на наборе  .
.
Таким образом 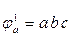
· Для контакта «b» определим проверочную функцию φºb.
Контакт входит в цепь 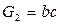 , а так же в сечение
, а так же в сечение  .
.
Сечение урезанное на контакте b, равно 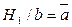
Цепь G2 существует при подаче входных переменных c = 1, b = 1, а сечение H1/b – при a = 0, т.е. цепь G2 и сечение H1/b одновременно существуют на наборе 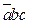 .
.
Таким образом 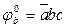
· Теперь для контакта «b» определим проверочную функцию φ¹b.
Контакт входит в сечение  , а так же в цепь
, а так же в цепь 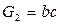 .
.
Цепь урезанная на контакте b, равна 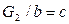 .
.
Сечение H1 существует при значениях переменных а = 0, b = 0, а цепь G2/b – при c = 1, т.е. сечение Н1 и цепь G2/b одновременно существуют на наборе 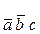 .
.
Таким образом 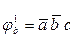
· Для контакта “c” определим проверочную функцию φºс
Контакт “с” входит в цепь 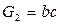 , а так же в сечение
, а так же в сечение  .
.
Сечение урезанное на контакте с, равно 
Цепь G2 существует при подаче входных переменных b=1, c=1, а сечения H2/c – при a = 0, т.е. цепь G2 и сечения H2/c одновременно существуют на наборе 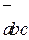 .
.
Таким образом 
· Теперь для контакта «с» определим проверочную функцию φ¹с.
Контакт “с” входит в цепь 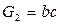 , а так же в сечение
, а так же в сечение  .
.
Цепь урезанная на контакте с, равна 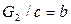 .
.
Сечение H2 существует при значениях переменных a = 0, с = 0, а цепь G2/с – при b = 1, т.е. сечение H2 и цепь G2/c одновременно существуют на наборе  .
.
Таким образом 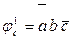
Теперь определим проверяющий тест Тп:
Тп= φºa φ¹a φºb φ¹b φºс φ¹c (2.1)
Подставим в выражение (2.1) полученные значения, проверяющих функций:
Тп= 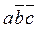 •
•  •
• 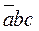 •
• 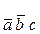 •
• 
Таким образом, проверочный тест будет представлять множество входных наборов.
Тп={ 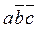 ,
,  ,
, 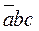 ,
, 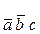 ,
,  }
}
Дата добавления: 2015-01-19; просмотров: 337; Мы поможем в написании вашей работы!; Нарушение авторских прав |