
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ГЛАВА 1. Расчет показателей надежности системы зажигания
Для любого случайно выбранного изделия невозможно заранее определить, будет ли оно надежно. Из двух двигателей одной марки в одном могут вскоре возникнуть отказы, а второй будет исправным длительное время.
Отказ – событие случайное. Поэтому для расчета показателей надежности используют методы теории вероятностей и математической статистики. Одним из условных понятий, используемых при расчетах показателей надежности, является ²наработка².
Наработкой называется продолжительность или объем работы изделия. Для двигателей наработку обычно измеряют в километрах пробега автомобиля или в часах (моточасах). В технической и учебной литературе можно встретить такие выражения: суточная наработка, наработка до первого отказа, наработка между отказами и т.д. Обычно применяется следующая буквенная индексация рассматриваемых далее в курсовой работе событий и понятий:
«F» (failure) - вероятность отказа;
«R» (reliability) - вероятность безотказной работы;
«Р» (probability) - вероятность.
Рассмотрим простейшие методы оценки случайной величины (СВ) примером которой является наработка на отказ. Исходные данные (приложение 1) - результаты наблюдений за изделиями или отчетные данные, которые выявили индивидуальные реализации случайных величин (наработки на отказ). Расчеты производятся в соответствии с примером, приведенным в данных методических указаниях. Результаты ниже изложенной методики расчета сводятся в таблицу 1.
Случайные величины- наработки на отказ (от 1 до 50)располагают в порядке возрастания их абсолютных значений:
L1 = Lmin; L2; L3;…;Li;…Ln-1; Ln = Lmax, (1)
где L1... Ln - реализации случайной величины L;
n - число реализаций.
L1=52,6; 53,7; 53,9;54,6;54,7;54,9;55,5;56,4;56,7;56,8;56,9;58,4;58,6;58,9;59,6;59,9;
60;60,4;60,9;61,3;61,9;62,5;62,8;63,6;63,9;64,7;64,9;65,2;65,3;65,4;65,8;65,9;67,8
Далее необходимо произвести точечные оценки СВ.
Среднее значение СВ:
 (2)
(2)
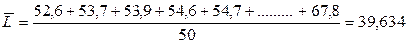
Размах СВ:
z = Lmax - Lmin. (3)
z =67,8 - 52,6=15,2
 Дисперсия:
Дисперсия:
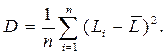 (4)
(4)

Среднеквадратическое отклонение s :
 . (5)
. (5)

Коэффициент вариацииv:
 (6)
(6)

В ТЭА различают случайные величины с малой вариацией (v ≤ 0,1), со средней вариацией (0,1 ≤ v ≤ 0,33) и с большой вариацией (v > 0,33).
Точечные оценки позволяют нам предварительно судить о качестве изделий и технологических процессов. Чем ниже средний ресурс и выше вариация (s, v, z), тем ниже качество конструкции и изготовления (или ремонта) изделия. Чем выше коэффициент вариации показателей технологических процессов ТЭА (трудоемкость, простои в ТО или ремонте, загрузка постов и исполнителей и др.), тем менее совершенны применяемые организация и технология ТО и ремонта.






 Вероятностные оценки СВ. При выполнении курсового проекта для составления сводной таблицы разбиваем размах СВ на несколько (не менее 8 и не более 11) равных по длине ∆L интервалов (см. табл.1). Далее производим группировку, т.е. определяем число случайных величин, попавших в первый (п1), второй (п2) и остальные интервалы. Это число называется частотой. Разделив частоту в каждом интервале на общее число случайных величин (п1 + п2 + ... + пп = п), определяют частость. Наглядное представление о величине частости дает графическое изображение гистограммы и полигонов распределения (рис.1).
Вероятностные оценки СВ. При выполнении курсового проекта для составления сводной таблицы разбиваем размах СВ на несколько (не менее 8 и не более 11) равных по длине ∆L интервалов (см. табл.1). Далее производим группировку, т.е. определяем число случайных величин, попавших в первый (п1), второй (п2) и остальные интервалы. Это число называется частотой. Разделив частоту в каждом интервале на общее число случайных величин (п1 + п2 + ... + пп = п), определяют частость. Наглядное представление о величине частости дает графическое изображение гистограммы и полигонов распределения (рис.1). 
Рис. 1.Графическое изображение случайной
величины (1-гистограмма, 2-полигон распределения).
Данное графическое изображение строится по данным о наработке и величине частости, которая рассчитывается по формуле:
wi = пi / п. (7)
w1 =3/50=0,06
w2=4/50=0,08
w3=6/50=0,12
w4 =17/50=0,34
w5=5/50=0,1
w6=5/50=0,1
w7=9/50=0,18
w8=1/50=0,02
Частость является эмпирической (опытной) оценкой вероятности Р, т.е. при увеличении числа наблюдений частость приближается к вероятности: wi → pi.
Полученные при группировке СВ результаты сводятся в таблицу (см. табл.1), данные которой имеют не только теоретическое, но и практическое значение. Например, по результатам наблюдений можно предположить, что у аналогичных изделий в тех же условиях эксплуатации и в интервале наработки 52-54 тыс. км может отказать около 6% изделий (wi ≈ pi = 0,06), в интервале 54-56 тыс. км - 8%, интервале 56-58 тыс. км - 12% и т.д. Следовательно, имея систематизированные данные по отказам, можно прогнозировать и планировать число воздействий (программу работ), потребности в рабочей силе, площадях, материалах и запасных частях.
Вероятность случайного события. В общем виде это отношение числа случаев, благоприятствующих данному событию, к общему числу случаев.
Вероятность отказа рассматривается не вообще, а за определенную наработку L:
F(L) = P{Li<L} =m(L)/n, (8)
где m(L) – число отказов к моменту наработки L;
п –число наблюдений (участвовавших в испытаниях изделий).
F1(L)=3/50=0,06
F2(L)=7/50=0,14
F3(L)=13/50=0,26
F4(L)=30/50=0,6
F5(L)=35/50=0,7
F6(L)=40/50=0,8
F7(L)=49/50=0,98
F8(L)=50/50=1
Вероятность отказа изделия при наработке L равна вероятности событий, при которых наработка до отказа конкретных изделий Li окажется менее L.
Отказ и безотказность являются противоположными событиями, поэтому:
R(L) = P{Li ≥ L} = n-m(L)/n. (9)
где n-m(L) - число изделий, не отказавших за L.
R1(L)=47/50=0,94
R2(L)=43/50=0,86
R3(L)=37/50=0,74
R4(L)=20/50=0,4
R5(L)=15/50=0,3
R6(L)=10/50=0,2
R7(L)=1/50=0,02
R8(L)=0/50=0
В примере расчета курсовой работы (см. табл.1) при L - 55 тыс. км имеем:
F(L) = P{Li<10} = L1+L2/n = m(L)/n =7/50 =0,14.
R(L) = P{Li ≥ 10} = n-m(L)/n = 50 – 7 / 50 =0,86.
Наглядное представление о СВ дает графическое изображение интегральных функции распределения вероятности отказа и вероятности безотказной работы (рис.2).



Рис. 2.Графическое изображение случайной величины
(3-интегральная функция вероятности отказов, 4- безотказной работы).
Следующей характеристикой случайной величины является плотность вероятности (например, вероятности отказа) f(L) – это функция, характеризующая вероятность отказа за малую единицу времени при работе узла, агрегата, детали без замены. Если вероятность отказа за наработку F(L) = т(L)/п, то, дифференцируя ее при п = const, получим плотность вероятности отказа:
 = (10)
= (10)
где dm/dL - элементарная "скорость", с которой в любой момент времени происходит приращение числа отказов при работе детали, агрегата без замены.
f1(L)=3/2/50=0,03
f2(L)=4/2/50=0,04
f3(L)=6/2/50=0,06
f4(L)=17/2/50=0,17
f5(L)=5/2/50=0,05
f6(L)=5/2/50=0,05
f7(L)=9/2/50=0,09
f8(L)=1/2/50=0,01
Таблица 1
| Определяемая величина | Обозначения и формулы расчета | Номера интервалов наработки до первого отказа | Всего | |||||||
| - | ||||||||||
| Границы интервала наработки (первый отказ), тыс. км. | ∆L | 52-54 | 54-56 | 56-58 | 58-60 | 60-62 | 62-64 | 64-66 | 66-68 | - |
| Значение середины интервала, тыс. км. | Li | - | ||||||||
| Число отказов в интервале | ni | |||||||||
| Число отказов к моменту наработки Li | m(L) | - | ||||||||
| Число работоспособных объектов к моменту наработки xi | n - m(L) | - | ||||||||
| Частость (вероятность) | wi = ni / n | 0,06 | 0,08 | 0,12 | 0,34 | 0,1 | 0,1 | 0,18 | 0,02 | 1,00 |
| Оценка накопленных вероятностей отказа | F1(L) = m(L)/n | 0,06 | 0,14 | 0,26 | 0,6 | 0,7 | 0,8 | 0,98 | - | |
| Оценка накопленных вероятностей безотказной работы | R1(L) = n-m(L)/n | 0,94 | 0,86 | 0,74 | 0,4 | 0,3 | 0,2 | 0,02 | - | |
| Плотность вероятности отказов | f1(L)= ni /∆L/ n | 0,03 | 0,04 | 0,06 | 0,17 | 0,05 | 0,05 | 0,09 | 0,01 | - |
| Интенсивность возникновения отказов | l(L)=f1(L)/R1(L) | 0,032 | 0,047 | 0,081 | 0,425 | 0,167 | 0,25 | 4,5 | - | - |
Вероятностная оценка случайных величин
Наглядное представление о вариации СВ дает графическое изображение дифференциальной функции т.е. закона распределения случайной величины (рис.3).


Рис. 3. Дифференциальная функция
распределения - закон распределения СВ
F(L) называют интегральной функцией распределения, f(L) - дифференциальной функцией распределения.
Имея значения F(x) или f(x), можно произвести оценку надежности и определить среднюю наработку до отказа:
 . (11)
. (11)
При оценке качества изделий, нормировании ресурсов, в системе гарантийного обслуживания применяют гамма - процентный ресурс Lγ. Это интегральное значение ресурса Lγ, которое вырабатывает без отказа не менее γ процентов всех оцениваемых изделий, т.е:

В ТЭА обычно принимаются γ = 80, 85, 90 и 95%.
Гамма - процентный ресурс используется при определении периодичности ТО по заданному уровню безотказности γ. Выражение LTO=Lγ означает, что обслуживание с периодичностью LTO гарантирует вероятность безотказной работы R ≥ γ и вероятность отказа F ≤ (1 - γ).
Если мы, основываясь на нашем примере, назначим периодичность профилактических работ ТО равную LTO = 55 тыс. км (см. табл.1), то примерно 7 изделий из 50 откажут ранее назначенного ТО, т.е. вероятность отказа составит 14%. Остальные 86% изделий имеют потенциальную наработку на отказ Li > 10 тыс. км. Следовательно, ТО им будет произведено ранее, чем они могут отказать, и вероятность их безотказной работы будет равна 0,86.
Для первых отказов невосстанавливаемых изделий и взаимно дополняющих событий (отказ - работоспособное состояние) имеет место условие F(L) + R(L) =1, т.е., зная вероятность отказа, можно определить вероятность безотказной работы и наоборот.
Важным показателем надежности является интенсивность отказов l(L) - условная плотность вероятности возникновения отказа невосстанавливаемого изделия, определяемая для данного момента времени при условии, что отказа до этого момента не было. Наглядное представление о величине изменения интенсивности отказов реализуется в виде графика (рис.4).


Рис.4. Изменение интенсивности отказов
Аналитически для получения l(L) необходимо элементарную вероятность dm/dL отнести к числу элементов, не отказавших к моменту L, т.е.
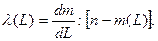 (12)
(12)
Так как вероятность безотказной работы R(L) = [n — m(L)]/n, то l(L) = (dm/dL)*(1/n R(L)). Учитывая, что f(L)=(1/n)(dm/dL), получаем:
l(L)=f(L)/R(L). (13)

Выше были рассмотрены закономерности изменения параметров технического состояния автомобилей по наработке и вариации параметров технического состояния. Эти закономерности достаточно точно характеризуют надежность новых агрегатов и узлов автомобилей, т.е. позволяют оценить среднюю наработку на отказ, вероятность отказа автомобиля при определенной наработке, ресурс агрегатов и др.
Для рациональной организации производства по ТО и ремонту в АТП необходимо, кроме того, знать, сколько автомобилей с отказами данного вида будет поступать в зону ремонта в течение часа, смены, недели, месяца, будет ли их количество постоянным или переменным и от каких факторов оно зависит, т.е. необходимо иметь информацию о надежности не только конкретного автомобиля, но и группы автомобилей, например автомобилей данной модели, колонны, в целом по АТП. При отсутствии этих сведений нельзя рационально организовать производство, т.е. определить необходимое число рабочих, размеры производственных площадей, перечень технологического оборудования, расход запасных частей и материалов. Взаимосвязи между показателями надежности автомобилей и суммарным потоком отказов для автомобиля и группы автомобилей изучают с помощью закономерностей ТЭА,которые характеризуют процесс восстановления, т.е. возникновения и устранения потока отказов и неисправностей изделий в зависимости от наработки.
Далее рассмотрим поведение восстанавливаемого изделия, т.е. агрегата, который после отказа подвергается ремонту и продолжает работать. Для этого в качестве исходных данных используем наработку до первого и до второго отказа (приложение 1). Так как агрегат является восстанавливаемым изделием, то после устранения 1-го отказа он продолжает работу, и по той же схеме возникают и устраняются 2-й, 3-й и последующие отказы. В курсовой работе мы ограничимся двумя отказами 50 исследуемых изделий. Ранее нами был полностью рассмотрен первый отказ, аналогично проводим исследования по второму отказу, для чего строим таблицу и вносим в нее все необходимые данные (табл.2). По результатам расчетов строим схему формирования процесса восстановления (рис.5) используя данные f1(L) (табл.1) и f2(L) (табл.2).


Рис.5. Схема формирования процесса восстановления
Таблица 2
Дата добавления: 2015-01-19; просмотров: 239; Мы поможем в написании вашей работы!; Нарушение авторских прав |