Устойчивость идеально связного массива грунта.

Рассмотрим условия равновесия идеально связного грунта (φ=0;с≠0).

Примем приближенно, что нарушение равновесия при некоторой предельной высоте h произойдет по плоской поверхности скольжения ас, наклоненной под углом α к горизонту (рис.4.15,б).

Рис. 4.15. Схемы сил, действующих на вертикальный массив связного грунnа (б)

Составим уравнение равновесия всех сил, действующих на оползающую призму abc. Действующей силой здесь будет вес Р призмы abc.

Принимая во внимание, что согласно рис. 4.15, б стороны призмы bc=h ctg α, получим

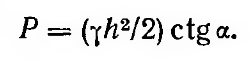
Силу Р разложим на нормальную и касательную к поверхности скольжения ас. Силами, сопротивляющимися скольжению, будут лишь силы сцепления с, распределенные по плоскости скольжения ac= h/sin α.

Так как в верхней точке с призмы abc давление будет равно нулю, а в нижней а — максимальным, то в среднем следует учитывать лишь половину сил сцепления, что элементарным путем позволяет прийти к решению, совпадающему для рассматриваемого случая со строгим решением теории предельного равновесия.

Составим уравнение равновесия, взяв сумму проекций всех сил на направление ас и приравняв ее нулю:

откуда

(T3)

Определим значение высоты h=h₀, соответствующей максимальному использованию сил сцепления. Очевидно, при этом sin2α=l и α = 45°. Тогда, полагая sin 2α=1 в выражении (T3) и решая его относительно h₀, получим

h₀=2c/γ

Таким образом, массив связного грунта может иметь вертикальный откос h₀ определенной высоты. При высоте, большей h₀, произойдет сползание призмы abc.

Отметим, что в природных условиях грунты обладают не только сцеплением, но и трением, и задача устойчивости откосов становится значительно более сложной, особенно при строгой ее постановке.