
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
для выполнения лабораторной работы 2
Задания и методические указания
по дисциплине «Физика»
для студентов всех форм обучения
направления подготовки 051000.62 Профессиональное обучение
(по отраслям)
Екатеринбург
РГППУ
Задания и методические указания для выполнения лабораторной работы 2 по дисциплине «Физика». Екатеринбург, ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2013. 16 с.
Составитель: к.ф.-м.н., доцент Анахов С.В.
Одобрены на заседании кафедры общей физики ЭлИн. Протокол № 1 от 10.09.2013 г.
Заведующий кафедрой ОФ
канд.физ.-мат. наук, доцент С.В. Анахов
Рекомендованы к печати научно-методической комиссией института электроэнергетики и информатики РГППУ. Протокол №1 от 14.10. 2013 г.
Председатель научно-методической
комиссии ЭлИн А.О. Прокубовская
© ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2013
© Анахов С.В., 2013
ЛАБОРАТОРНАЯ РАБОТА 2 «ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ»
Цель лабораторной работы:
· определение ускорения свободного падения с помощью математического и физического маятников.
Задачи лабораторной работы:
· изучение процессов и параметров свободных колебаний;
· изучение параметров математического и физического маятников.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Маятниковые системы начали употребляться в Европе со времен Галилео Галилея (конец ХVI – начало ХVII века) для точного измерения небольших промежутков времени путем подсчёта произведенного ими числа качаний. В эти годы Галилей опубликовал исследование колебаний маятника в котором было заявлено, что период его колебаний не зависит от амплитуды. Он также обнаружил, что периоды колебаний маятника соотносятся как квадратные корни из его длины. Результаты Галилея привлекли внимание Христиана Гюйгенса, который изобрёл часы с маятниковым регулятором (1657), после чего появилась возможность точных измерений в экспериментальной физике (Галилей, например, при изучении законов падения считал удары собственного пульса). В 1673 году Гюйгенс опубликовал классический труд по механике «Маятниковые часы». В первых его четырёх частях Гюйгенс исследовал ряд проблем, связанных с движением маятника. В настоящее время принято рассматривать две физические модели механических маятников.
Математический маятник — осциллятор, представляющий собой механическую колебательную систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения (рис.1).

Рис.1. Математический маятник
При небольших углах отклонения (малом углеqи высоте подъема h<<y1 – рис.1) физический маятник совершает гармонические колебания. Период колебаний Т математического маятника равен:
 , (1)
, (1)
где  l – длина нити математического маятника (расстояние от точки подвеса до центра масс шарика (l = y1 на рис.1).
l – длина нити математического маятника (расстояние от точки подвеса до центра масс шарика (l = y1 на рис.1).
Таким образом, для определения величины  с помощью математического маятника достаточно измерить его период колебаний Т и длину l, после чего рассчитать ускорение свободного падения
с помощью математического маятника достаточно измерить его период колебаний Т и длину l, после чего рассчитать ускорение свободного падения  по формуле:
по формуле:
 , (2)
, (2)
которая следует из (1).
Физический маятник– твёрдое тело, совершающее колебания относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр масс этого тела (рис.2).

Рис.2. Физический маятник
При небольших углах отклонения (малом угле φ– рис.2) физический маятник совершает гармонические колебания, период которых определяется по формуле:
 , (3)
, (3)
где m - масса физического маятника, l - расстояние от оси вращения  до его центра масс С (l =
до его центра масс С (l =  на рис.2), J - момент инерции физического маятника относительно оси вращения.
на рис.2), J - момент инерции физического маятника относительно оси вращения.
Проводить измерения  с помощью произвольного физического маятника, опираясь на формулу (3), достаточно затруднительно, так как при этом необходимо знать точное значение его момента инерции, положение центра масс и массу. Однако существует прибор, называемый оборотным маятником, при использовании которого задача определения ускорения свободного падения сводится к измерению периода колебаний и некоторого расстояния между элементами конструкции оборотного маятника.
с помощью произвольного физического маятника, опираясь на формулу (3), достаточно затруднительно, так как при этом необходимо знать точное значение его момента инерции, положение центра масс и массу. Однако существует прибор, называемый оборотным маятником, при использовании которого задача определения ускорения свободного падения сводится к измерению периода колебаний и некоторого расстояния между элементами конструкции оборотного маятника.
Оборотный маятник устроен следующим образом (рис. 3). На стержне (1) закрепляются два груза (2,3). Стержень имеет две оси вращения (4,5), расположенные по обе стороны от центра масс системы. Оси вращения для уменьшения трения выполняют в виде треугольных призм из твердого материала, которые следует устанавливать на специальную опору, закрепленную на подставке.
 Рис.3
Рис.3
|
Оборотный маятник регулируется таким образом, чтобы период его колебаний при установке на одной призме равнялся периоду колебаний его на другой призме. Регулировка производится путем изменения взаимного расположения грузов и призм на стержне.
Выведем формулу периода колебаний оборотного маятника. Согласно формуле Гюйгенса - Штейнера. Момент инерции J маятника относительно произвольной оси вращения равен:
J = Jc+ml2, (4) (4)
где Jс – момент инерции относительно оси вращения, проходящей через центр масс, m - масса маятника, а l - расстояние от оси вращения до центра масс. После подстановки (4) в (2) формула для периода колебаний физического маятника примет вид:
 .
.
Поскольку оборотный маятник имеет равные периоды колебаний на обеих призмах (осях), полученное соотношение используем для двух расположений маятника:
 (5)
(5)
Здесь l1 и l2 - расстояния от центра масс маятника до ребра первой и второй призмы соответственно.
Возведем формулы (5) в квадрат и умножим на знаменатели правых частей:

Вычтем из первого равенства второе и сократим на m:
 ,
,

Применим формулу разности квадратов в правой части:
 (6)
(6)
Если в (6) l1 ≠l2, что означает несимметричность расположения призм относительно центра масс маятника, то, сокращая на  , получаем:
, получаем:
 (7)
(7)
Поскольку призмы расположены по разные стороны от центра масс, то  где
где 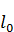 - расстояние между соответствующими ребрами призм (осями колебаний), или приведенная длина оборотного маятника.
- расстояние между соответствующими ребрами призм (осями колебаний), или приведенная длина оборотного маятника.
На основании (7) легко записывается выражение для периода колебаний оборотного маятника:
 (8)
(8)
и формула для определения g:
 (9)
(9)
Еще раз подчеркнем, что в случае (симметричное расположение осей колебаний относительно центра масс маятника), формулы (8) и (9) не являются справедливыми. Величина периода колебаний в этом случае зависит не только от l0 и  , но и от момента инерции маятника.
, но и от момента инерции маятника.
2.ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
Лабораторный стенд изображен на рисунке 4 и включает в себя математический маятник (шарик на нити – 1) и физический маятник (оборотный маятник – 2), а также оптоэлектрический датчик 3. К приборам и принадлежностям относятся также компьютер с необходимым программным обеспечением, соединительный кабель 4 для подключения оптоэлектрического датчика к компьютеру, измерительная линейка 5.
Оптоэлектрический датчик размещают таким образом, чтобы качающиеся маятники (шарик, либо несущий стержень оборотного маятника) пересекали оптическую ось датчика. При запуске измерений датчик фиксирует моменты перекрытия и открытия оптической оси датчика. Период колебаний определяется по интервалу между передними либо задними фронтами ближайших четных, либо нечетных импульсов.

Рис.4. Лабораторный стенд (маятник Обербека)
Указания по технике безопасности:
· Перед выполнением работы получите инструктаж у лаборанта или преподавателя.
· Соблюдайте общие правила техники безопасности работы в лаборатории «Физика».
· Осторожно обращайтесь с оборотным маятником. Не допускайте падений и ударов маятника, это может нарушить его регулировку.
3.ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
3.1. Порядок выполнения работы с использованием компьютера
1.Внесите в таблицу 1 (см. образец отчета – приложение А) данные о средстве измерения (линейка). Определите длину подвеса математического маятника l и приведенную длину оборотного маятника l0, измерив линейкой расстояние от подвеса до середины шарика и расстояние между двумя призмами оборотного маятника на Вашей лабораторной установке.
2.Соберите лабораторную установку, поместив оптический датчик на пути качания выбранного маятника.
3.Подключите оптоэлектрический датчик к USB– входу компьютера.
4.После включения компьютера запустите программу «Практикум по физике». На панели устройств выберете соответствующий сценарий проведения эксперимента (Alt+C) или кнопкой  .
.
5.Запустите измерения для выбранного датчика (Ctrl+S) или кнопкой  и приведите в движение математический/физический маятник.
и приведите в движение математический/физический маятник.
6.После записи нескольких (5-6) пересечений оптической оси датчика остановите измерения (Ctrl+T) или кнопкой  .
.
7.Проведитеобработку полученных данных в соответствии со сценарием, для чего:
· выделите область из 5-6 импульсов перекрытия для ее детального просмотра с увеличенным масштабом (Alt+левая кнопка мыши) – рис. 5;
· измерьте период колебаний маятника по передним или задним фронтам соседних четных (либо нечетных) импульсов перекрытий путем постановки желтого (левая клавиша мыши) и зеленого маркера (правая клавиша мыши) на соответствующие фронты импульса перекрытия. После каждого измерения нажмите кнопку  в верхнем правом углу (рис.5) для сохранения результата в электронной таблице (рис.6).
в верхнем правом углу (рис.5) для сохранения результата в электронной таблице (рис.6).

Рис.5. Определение периода колебаний на компьютере

Рис.6. Таблица экспериментальных данных (<T>=1,00997 c)
8.Выполните измерения периода 5 раз, используя различные фронты разных импульсов. Результаты измерений запишите в таблицу 2 (см. образец отчета – приложение А). Сохраните электронный вариант таблицы (рис.6) под своим именем (Иванов_Петров_Сидоров_1.xls – кнопкой  ) или (Иванов_Петров_Сидоров_1.bmp – кнопкой
) или (Иванов_Петров_Сидоров_1.bmp – кнопкой  ) в указанной преподавателем директории на компьютере. Очистите данные таблицы кнопкой
) в указанной преподавателем директории на компьютере. Очистите данные таблицы кнопкой  .
.
9.Повторите пп. 5-8 для другого маятника. Результаты измерений запишите в таблицу 3. Сохраните электронный вариант таблицы в указанной преподавателем директории на компьютере под своим именем (Иванов_Петров_Сидоров_2.xls или Иванов_Петров_Сидоров_2.bmp).
10.Используя полученные результаты, определите ускорение свободного падения  для каждого из пяти опытов как для математического, так и для физического (оборотного) маятников.
для каждого из пяти опытов как для математического, так и для физического (оборотного) маятников.
11.Найдите средние значения ускорения свободного падения для этих экспериментов (<  м> и <
м> и <  ф>).
ф>).
12.Используя правила оценки погрешностей косвенных измерений, определите погрешности оценок ускорения свободного падения для этих экспериментов (D  м и D
м и D  ф).
ф).
13.Запишите, используя правила округления, окончательный результат работы в виде
 м = <
м = <  м>±D
м>±D  м,м/с2
м,м/с2
 ф = <
ф = <  ф>±D
ф>±D  ф,м/с2
ф,м/с2
14.Сравните полученные результаты (в том числе со справочными данными) и сформулируйте вывод.
3.2.Порядок выполнения работы без использования компьютера
1.Внесите в таблицу 1 (см. образец отчета) данные о средствах измерения (линейка и секундомер). Определите длину подвеса математического маятника l и приведенную длину оборотного маятника l0, измерив линейкой расстояние от подвеса до середины шарика и расстояние между двумя призмами оборотного маятника на Вашей лабораторной установке.
2.Приведите в движение один из маятников и секундомером измерьте период его колебаний, фиксируя момент прохождения им вертикального положения в определённом направлении (не менее 6 раз).
3.Результаты измерений запишите в таблицу 2 (см. образец отчета).
4.Повторите пп. 2-3 для другого маятника. Результаты измерений запишите в таблицу 3.
5.Используя полученные результаты, определите ускорение свободного падения  kдля каждого из пяти опытов как для математического, так и для физического (оборотного) маятников.
kдля каждого из пяти опытов как для математического, так и для физического (оборотного) маятников.
6.Найдите средние значения ускорения свободного падения для этих экспериментов (<  м>и <
м>и <  ф>).
ф>).
7.Используя правила оценки погрешностей косвенных измерений, определите погрешности оценок ускорения свободного падения для этих экспериментов (D  ми D
ми D  ф).
ф).
4. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
· Расчет случайной погрешности 
Среднеквадратическое отклонение:
 = ........... м/с2 ,
= ........... м/с2 ,
где n - число измерений.
 ........... м/с2 ,
........... м/с2 ,
где  - коэффициент Стьюдента, определенный для доверительной вероятности р=0,95 (
- коэффициент Стьюдента, определенный для доверительной вероятности р=0,95 (  =2,77 для n=5).
=2,77 для n=5).
· Расчет систематической погрешности 
 ,
,
где  - предел основной погрешности линейки, l – длина подвеса (приведенная длина) маятника,
- предел основной погрешности линейки, l – длина подвеса (приведенная длина) маятника, 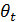 - предел основной погрешности датчика времени (при использовании компьютера
- предел основной погрешности датчика времени (при использовании компьютера 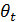 =0,01 с), предел основной погрешности секундомера (при работе без компьютера),
=0,01 с), предел основной погрешности секундомера (при работе без компьютера),  - среднее значение периода измерений (см. электронную таблицу – рис.4).
- среднее значение периода измерений (см. электронную таблицу – рис.4).
· Расчет абсолютной погрешности 

8.Запишите, используя правила округления, окончательный результат работы в виде
 м = <
м = <  м>±D
м>±D  м,м/с2
м,м/с2
 ф = <
ф = <  ф>±D
ф>±D  ф,м/с2
ф,м/с2
9.Сравните полученные результаты и сформулируйте вывод.
10.Оформите отчет по лабораторной работе (Приложение А).
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение колебательного процесса.
2. Дайте определения для основных параметров колебаний.
3. Что такое гармонические колебания?
4. Что такое математический маятник?
5. Что такое физический маятник?
6. Что такое оборотный маятник?
7. Что называется приведенной длиной физического маятника?
8. Напишите уравнение движения при гармонических колебаниях.
9. Выведите формулу для периода колебаний математического маятника.
10. Выведите формулу для периода колебаний физического маятника.
6. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Ивлиев А.Д. Физика: Учебное пособие для вузов. СПб: Лань, 2008. 671 с.
Ивлиев А.Д. Физика. Квантовая механика. Физика атомов и молекул. Физика твердого тела. Физика атомного ядра и элементарных частиц: учеб. пособие для вузов. Екатеринбург : Издательство УГТУ-УПИ, 2005. 247 с.
Ивлиев А.Д. Классическая механика. Специальная теория относительности. Электричество и магнетизм. Колебания и волны. Молекулярная физика и термодинамика: учеб. пособие для вузов. Екатеринбург : Издательство УГТУ-УПИ, 2004. 617 с.
Ивлиев А.Д. Физика: Классическая механика. Специальная теория относительности. Электричество и магнетизм. Колебания и волны. Молекулярная физика и термодинамика: учеб. пособие для вузов. Екатеринбург: Издательство УГТУ-УПИ, 2005. 617 с.
Арсентьев В. В [и др.] Курс физики. В 2 т. Т. 1: учебник для вузов. СПб. Лань, 2007. 572 с.
Приложение А
Форма отчета по лабораторной работе
ОТЧЕТ
по лабораторной работе 2
Измерение ускорения свободного падения с помощью
математического и физического маятников
студент ______________
группа _______________
Дата ________________
Преподаватель _____________
РГППУ
1.Расчетные формулы:
Ускорение свободного падения, определённое с помощью математического маятника:
 ,
,
где  – длина подвеса (расстояние от точки подвеса до центра шарика),
– длина подвеса (расстояние от точки подвеса до центра шарика),  - период колебаний.
- период колебаний.
Ускорение свободного падения, определённое с помощью физического маятника:

где  - приведенная длинаоборотного маятника (расстояние между соответствующими ребрами призм (осями колебаний)).
- приведенная длинаоборотного маятника (расстояние между соответствующими ребрами призм (осями колебаний)).
2.Средства измерений и их характеристики.
Таблица1.
| Средство измерения, его тип и номер | Цена деления шкалы | Предел измерения | Предел основной погрешности |
| Линейка | |||
| Секундомер* |
*-при выполнении работы без использования компьютера.
Математический маятник:  …….мм.
…….мм.
Физический маятник: 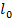 =……мм.
=……мм.
3.Результаты измерений и математическая обработка результатов измерений.
3.1.Определение ускорения свободного падения с помощью математического маятника.
Таблица2.
| к, номер опыта | Период математического маятника Тмк, с | Ускорение
свободного падения
 ,
м/с2 ,
м/с2
| < 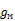 >- >-  ,
м/с2 ,
м/с2
| (< 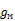 >- >-  )2,
(м/с2)2 )2,
(м/с2)2
|
<  >= >=
| 
|
· Расчет случайной погрешности 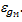
 = ........... м/с2 ,
= ........... м/с2 ,
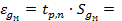 ........... м/с2.
........... м/с2.
· Расчет систематической погрешности 
 ........... м/с2.
........... м/с2.
Расчет абсолютной погрешности 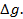
 =........... м/с2.
=........... м/с2.
· Запись окончательного результата
 = <
= <  >±D
>±D  =........... м/с2,при доверительной вероятности р=0,95.
=........... м/с2,при доверительной вероятности р=0,95.
3.2.Определение ускорения свободного падения с помощью физического маятника.
Таблица3.
| к, номер опыта | Период физиического маятника Тфк, с | Ускорение
свободного падения
 фк,
м/с2 фк,
м/с2
| <  ф>- ф>-  фк,
м/с2 фк,
м/с2
| (<  ф>- ф>-  фк)2,
(м/с2)2 фк)2,
(м/с2)2
|
<  >= >=
| 
|
· Расчет случайной погрешности 
 = ........... м/с2 ,
= ........... м/с2 ,
 ........... м/с2.
........... м/с2.
· Расчет систематической погрешности 
 ........... м/с2.
........... м/с2.
· Расчет абсолютной погрешности 
 =........... м/с2.
=........... м/с2.
· Запись окончательного результата
 = <
= <  >±D
>±D  =........... м/с2,при доверительной вероятности р=0,95.
=........... м/с2,при доверительной вероятности р=0,95.
4.Вывод:
Задания и методические указания
для выполнения лабораторной работы 2
по дисциплине «Физика»
Подписано в печать _______. Формат 60´84/16. Бумага для множ. аппаратов.
Печать плоская. Усл. печ. л. __. Уч.-изд. л.__. Тираж ____ экз. Заказ № ____.
ФГАОУ ВПО «Российский государственный профессионально-педагогический университет». Екатеринбург, ул. Машиностроителей, 11.
Ризограф ФГАОУ ВПО РГППУ. Екатеринбург, ул. Машиностроителей, 11.
Дата добавления: 2015-01-29; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Для выполнения лабораторной работы 3 | | | СЕТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ. ОСНОВНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ И ХАРАКТЕРИСТИКИ. |