
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для выполнения лабораторной работы 3
Задания и методические указания
по дисциплине «Физика»
для студентов всех форм обучения
направления подготовки 051000.62 Профессиональное обучение
(по отраслям)
Екатеринбург
РГППУ
Задания и методические указания для выполнения лабораторной работы № 3 по дисциплине «Физика». Екатеринбург, ФГАОУ ВПО «Рос. гос. проф.-пед. ун-т», 2013. 17 с.
Составитель: к.ф.-м.н., доцент Анахов С.В.
Одобрены на заседании кафедры общей физики ЭлИн. Протокол № 1 от 10.09.2013 г.
Заведующий кафедрой ОФ
канд.физ.-мат. наук, доцент С.В. Анахов
Рекомендованы к печати научно-методической комиссией института электроэнергетики и информатики РГППУ. Протокол №1 от 14.10. 2013 г.
Председатель научно-методической
комиссии ЭлИн А.О. Прокубовская
© ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2013
© Анахов С.В., 2013
ЛАБОРАТОРНАЯ РАБОТА 3 «ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА»
Цель лабораторной работы:
· экспериментально и теоретически определить, как изменяется момент инерции вращающегося тела при изменении распределения массы относительно неподвижной оси вращения.
Задачи лабораторной работы:
· изучение законов динамики вращательного движения твердого тела;
· изучение зависимости момента инерции твердого тела от распределения массы относительно неподвижной оси вращения.
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Момент инерции твердого тела - это скалярная физическая величина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении. С точки зрения аналогий между характеристиками вращательного и поступательного движения момент инерции аналогичен массе тела при его поступательном движении.
Момент инерции тел простой геометрической формы можно вычислить по простым формулам. Например, момент инерцииматериальной точки относительно оси вращения – произведение массы этой точки m на квадрат расстояния от оси r (рис.1, а):
 (1)
(1)
Единица момента инерции – килограмм×метр в квадрате.
Рис.1.Определение момента инерции
Для твердых тел, размерами которых пренебречь нельзя, момент инерции зависит как от распределения массы по объему тела, так и от положения и направления оси вращения.
Для тела, представимого в качестве совокупности материальных точек, формула момента инерции:
 , (2)
, (2)
где  - масса i-ой точки, ri – расстояние от i-ой точки до оси вращения.
- масса i-ой точки, ri – расстояние от i-ой точки до оси вращения.
Момент инерции тел, имеющих сложную форму, можно определить путем интегрирования по объему (рис.1, б):
 (3)
(3)
где r - плотность однородного тела, V – его объем,
либо путем разбиения тела на более простые части, с последующим суммированием моментов инерций отдельных частей:
 . (4)
. (4)
В ситуации, когда ось вращения не проходит через центр масс (центр инерции) тела, для расчета момента инерции применяется теорема Штейнера:
момент инерции тела относительно произвольной оси (О1О1') равен моменту инерции J0 относительно параллельной оси (ОО'), проходящей через центр инерции, сложенной с величиной ma2, где a - расстояние между осями (рис.1, в).
 (5)
(5)
Согласно основному уравнению динамики вращательного движения угловое ускорение e, которое приобретает тело, прямо пропорционально результирующему моменту всех действующих на него внешних сил M, приложенных к телу, и обратно пропорциональна моменту инерции тела J относительно некоторой оси:
 . (6)
. (6)
Знание моментов инерции элементов машин и механизмов необходимо для проведения расчетов, связанных с их вращательным движением. В этом заключается прикладное значение изучения методов определения моментов инерции.
Для экспериментального определения моментов инерции используют устройство под названием маятник Обербека.
Маятник Обербека (рис.2) представляет собой крестовину 1, на четырех взаимно перпендикулярных стержнях которой располагаются четыре подвижных (вращаемых) груза массой m каждый. Крестовина закреплена на вращающейся оси со шкивом 3, для определения расстояния от центра масс грузов до оси вращения используется линейка 4. На шкив намотана нить 5 с грузиком 6 массой m0. Под действием силы тяжести груза 6 нить разматывается с оси и вызывает вращательное движение крестовины. На оси крестовины располагается датчик 7 угловой скорости вращения маятника. К приборам и принадлежностям относятся также компьютер с необходимым программным обеспечением и соединительный кабель для подключения датчика угловой скорости к компьютеру.
При изменении расстояния перемещаемых грузов от оси крестовины маятника Обербека угловое ускорение e крестовины тем меньше, чем больше момент инерции тела J относительно оси вращения. Определить величину углового ускорения е можно с помощью уравнения динамики вращательного движения:
Je = М, (7)
где М – момент сил, действующих на маятник, J – момент инерции маятника.

Рис.2. Лабораторный стенд (маятник Обербека)
Ускорение а груза т0 связано с угловым ускорением e формулой
a = ed/ 2, (8)
где d – диаметр диска, на который намотана нить.
Вращательный момент силы М, действующий на маятник, определяется выражением:
М = Td/2 – МТ , (9)
где Т – сила натяжения нити, МТ – момент сил трения в оси.
С другой стороны, сила Т вместе с силой тяжести вызывает движение груза с ускорением а:
m0a = m0g – T (10)
Отсюда момент силы можно выразить так:
М = m0(g – a)d/2 – Мт (11)
Если подставить (11) в (7), воспользовавшись формулой (8), получим выражение:
Je = m0(g –ed/2)d/2 – MT,
после преобразования которого уравнение динамики маятника Обербека приобретет вид:
(J + m0d2/4)e = m0gd/2 –MT (12)
Теоретическое значение момента инерции крестовины с 4-мя грузами
J = J0 + 4Jm + 4mr2. (13)
Здесь J0 - суммарный момент инерции крестовины без грузов, Jm - момент инерции подвижного груза относительно оси, проходящей через его центр масс и параллельной оси вращения крестовины, r - расстояние от оси вращения маятника до центра масс грузов, m – масса каждого из четырех подвижных грузов.
ВеличинаJm + mr2 в (13) есть момент инерции подвижного грузаотносительно оси вращения крестовины. При этом использована теорема Гюйгенса - Штейнера: момент инерции тела относительно любой оси вращения равен моменту инерции тела относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.
В первой части данной работы необходимо определить постоянную часть момента инерции маятника Обербека – величину Jc = J0 + 4Jm, не зависящую от расположения подвижных вращаемых грузов на крестовине.
Поскольку величина момента трения в оси неизвестна, воспользоваться для этого впрямую формулой (12) нельзя.
Если рассмотреть два положения грузов относительно оси маятника – r1 и r2, то можно переписать дважды (12). С учетом (13) эти выражения приобретут вид:
(J0 + 4Jт + 4тr12 + т0 d2/4)e1 = m0gd/2 – МТ (14)
(J0 + 4Jm + 4mr22 + m0d2/4) e2 = m0gd/2 – MT (15)
Равенство правых частей этих равенств означает и равенство их левых частей:
(J0 + 4Jт + 4mr12 + m0 d2/4)e1 = (J0 + 4Jm + 4mr22 + m0d2/4) e2 (16)
Отсюда можно найти искомую величину Jc:
 (17)
(17)
Во второй части работы определяется момент инерции вращаемых грузов Jгр=4Jт + 4mr2 в зависимости от расстояния до оси вращения. Воспользуемся для этого формулой (15), представив её в упрощенном виде:
(J0 + Jгр)e2 = m0gd/2 (18)
В выражении (18) мы пренебрегли моментом силы трения МТ по сравнению с моментом силы тяжести m0gd/2 и моментом инерции шкива т0 d2/4. Для определения Jгр надо определить суммарный момент инерции крестовины без грузов J0. Для этой цели надо произвести измерения, сняв грузы с крестовины. В этом случае момент инерции уменьшится и крестовина будет вращаться с большим угловым ускорением e3 согласно уравнению:
J0  e3 = m0gd/2 (19)
e3 = m0gd/2 (19)
Совместное решение уравнений (18) и (19) позволяет определить искомый момент инерции подвижных грузов, находящихся на расстоянии r от оси вращения:
 (20)
(20)
Поскольку постоянная составляющая Jт момента инерции грузов (Jгр=4Jт + 4mr2) много меньше зависящей от расстояния r для оценки точности экспериментальных расчетов можно использовать теоретическую формулу:
 (21)
(21)
Как следует из уравнения (12), угловое ускорение маятника – постоянная для выбранного положения груза величина, т.е. вращение является равноускоренным. В этом случае угловое ускорение можно определять по углу наклона графика угловой скорости от времени (  ). Все остальные величины задаются в ходе работы.
). Все остальные величины задаются в ходе работы.
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
Для выполнения первой части работы необходимо выполнить две серии измерений угловых ускорений маятника при двух различных удаленностях грузов на крестовине от ее оси – r1 и r2. Для определения этих расстояний на лабораторном стенде установлена линейка (рис.3). На практике положение грузов на крестовине меняется с помощью их перемещения по резьбовым спицам крестовины. Фиксация грузов в каждой серии измерений осуществляется путем законтрирования двух резьбовых половин каждого груза выбранном положении.
| r1 |

Рис.3. Определение расстояния до центра масс подвижных грузов
1.Перенесите в таблицу 1 (см. приложение А) данные о средствах измерения, в таблицу 2 – данные о массе грузов m и m0 и выбранных Вами удаленностях грузов на крестовине от её оси – r1 и r2.
2.Соберите лабораторную установку, зафиксировав подвижные грузы (рис. 3) на выбранном расстоянии от оси вращения маятника. Подключите датчик угловой скорости к USB - входу компьютера с помощью соединительного кабеля. При установке грузов отметка на линейке, соответствующая выбранному радиусу, должна быть видна сквозь зазор между грузами, т.е. совпадать с положением центра масс грузов.
3.После включения компьютера запустите программу практикума. На панели устройств выберите соответствующий сценарий проведения эксперимента (Alt+С)  .
.
4.Запустите измерения (Ctrl+S) или кнопкой  и сразу, непосредственно вслед за запуском приведите в движение маятник, предоставив ему возможность вращаться под действием веса груза 6 (рис.2). Следите за тем, чтобы при спуске груз не раскачивался из стороны в сторону, т.к. в противном случае сила натяжения нити будет непостоянна, что приведёт к неравномерному набору скорости.
и сразу, непосредственно вслед за запуском приведите в движение маятник, предоставив ему возможность вращаться под действием веса груза 6 (рис.2). Следите за тем, чтобы при спуске груз не раскачивался из стороны в сторону, т.к. в противном случае сила натяжения нити будет непостоянна, что приведёт к неравномерному набору скорости.
5.После того, как нить полностью размотается и начнет наматываться обратно на барабан (замедление вращения маятника) остановите измерения (Ctrl+T) или кнопкой  . После этого выделите область возрастания графика для ее детального просмотра с увеличенным масштабом (Alt+левая кнопка мыши).
. После этого выделите область возрастания графика для ее детального просмотра с увеличенным масштабом (Alt+левая кнопка мыши).
ВНИМАНИЕ! Если Вы остановили измерения достаточно поздно, то на зарегистрированном графике зависимости угловой скорости от времени будет несколько участков с монотонным возрастанием и уменьшением скорости. Т.к. раскачка груза m0 при его первом спуске минимальна, то для более точного определения ускорения следует использовать участок графика, соответствующий именно первому спуску груза.
6.Нормальный вид регистрируемого графика показан на рисунке 4. Следует обратить внимание, что датчик угловой скорости имеет отличающийся от нуля нижний предел измерения. На графике это иногда выглядит как ступенька (резкий скачок) перед участком плавного роста угловой скорости. Это происходит из-за того, что в течение одного периода опроса датчика его оптическую ось должен перекрыть и снова открыть по крайней мере один зуб крыльчатки. Чтобы уменьшить нижний предел измерения датчика, нажмите кнопку  и выберите большее значение периода оцифровки. Однако, чрезмерное увеличение периода оцифровки снижает точность измерений, поэтому период оцифровки следует выбирать таким, чтобы на монотонном участке графика, выбираемом для обработки, было не менее 15 – 20 точек. Оптимальным будет выбор значения периода оцифровки в 200 мс.
и выберите большее значение периода оцифровки. Однако, чрезмерное увеличение периода оцифровки снижает точность измерений, поэтому период оцифровки следует выбирать таким, чтобы на монотонном участке графика, выбираемом для обработки, было не менее 15 – 20 точек. Оптимальным будет выбор значения периода оцифровки в 200 мс.

Рис.4. График зависимости угловой скорости вращения шкива от времени
7.Установите зелёный вертикальный маркер (правая кнопка мыши) в начале участка графика с монотонным возрастанием, а жёлтый вертикальный маркер (левая кнопка мыши) в конце этого участка (рис.4). Для внесения экспериментальных точек выделенной области графика в таблицу обработки нажмите кнопку  . В открывшемся окне «Обработка» (рис.5) перейдите на вкладку «График», в котором строится по экспериментальным точкам зависимость угловой скорости от времени. Для аппроксимации этой зависимости линейной функцией вида Y=Ax+B нажмите кнопку
. В открывшемся окне «Обработка» (рис.5) перейдите на вкладку «График», в котором строится по экспериментальным точкам зависимость угловой скорости от времени. Для аппроксимации этой зависимости линейной функцией вида Y=Ax+B нажмите кнопку  (рис.6). В верхнем левом углу окна появится соответствующее уравнение аппроксимирующей прямой (рис.7). Определите по его угловому коэффициенту значение углового ускорения маятника.
(рис.6). В верхнем левом углу окна появится соответствующее уравнение аппроксимирующей прямой (рис.7). Определите по его угловому коэффициенту значение углового ускорения маятника.

Рис.5. Таблица регистрируемых значений угловой скорости

Рис.6. График обрабатываемых значений угловой скорости

Рис.7. Аппроксимирующая линейная зависимость угловой
скорости и определение углового ускорения (e =3,12 с-2)

Рис.8. Таблица аппроксимированных значений угловых ускорений
и данные их статистическая обработки (<e >=3,10 с-2, S<e >=0,013 с-2)
8.Повторите эксперимент в соответствии с пп. 4-7 еще 4 раза. Результаты измерений запишите в таблицу 3 или на вкладку «Статистика», куда при нажатии клавиши  фиксируются угловой коэффициент и свободный член аппроксимирующей прямой, а также рассчитывается их среднее значение <e > и среднеквадратическое отклонение S<e > (рис.8). При каждом последующем запуске измерений соглашайтесь с предложением программы очистить таблицу накопленных данных. Сохраните электронный вариант таблицы под своим именем (Иванов_Петров_Сидоров_1.xls) в указанной преподавателем директории на компьютере, после чего очистите данные в таблице программы путем нажатия на кнопку
фиксируются угловой коэффициент и свободный член аппроксимирующей прямой, а также рассчитывается их среднее значение <e > и среднеквадратическое отклонение S<e > (рис.8). При каждом последующем запуске измерений соглашайтесь с предложением программы очистить таблицу накопленных данных. Сохраните электронный вариант таблицы под своим именем (Иванов_Петров_Сидоров_1.xls) в указанной преподавателем директории на компьютере, после чего очистите данные в таблице программы путем нажатия на кнопку  .
.
9.Измените расположение грузов на крестовине, зафиксировав их на другом расстоянии от оси маятника. Выполните вторую серию экспериментов в новом положении грузов по пп. 4-8. Результаты измерений запишите в таблицу 2. Сохраните электронный вариант таблицы под своим именем (Иванов_Петров_Сидоров_2.xls) в указанной преподавателем директории на компьютере, после чего очистите данные в таблице программы путем нажатия на кнопку  .
.
10.Для выполнения второй части работы снимите грузики с крестовины, после чего повторите измерения по пп. 4-8. Поскольку угловое ускорение e3 в этом случае существенно возрастает, измените масштаб графика зависимости угловой скорости от времени (рис.4) путем нажатия на кнопку  и задания максимального значения угловой скорости 50 рад/с. Результаты измерений запишите в таблицу 3. Сохраните электронный вариант таблицы под своим именем (Иванов_Петров_Сидоров_3.xls) в указанной преподавателем директории на компьютере.
и задания максимального значения угловой скорости 50 рад/с. Результаты измерений запишите в таблицу 3. Сохраните электронный вариант таблицы под своим именем (Иванов_Петров_Сидоров_3.xls) в указанной преподавателем директории на компьютере.
11.Произведите обработку результатов измерений.
12.Оформите отчет по лабораторной работе (приложение А).
Указания по технике безопасности
· Перед выполнением работы получите инструктаж у лаборанта.
· Соблюдайте общие правила техники безопасности работы в физической лаборатории.
· Шнур наматывать на шкив виток витку, вращая крестовину против часовой стрелки до перемещения груза 6 (рис. 2) в верхнее положение.
4. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
1.Используя полученные результаты, определите среднее угловые ускорения и их погрешности для каждой серии экспериментов.
2.Определите момент инерции <Jc> по формуле (17), подставив в неё данные из таблицы 2 (см. приложение А) и средние значения угловых ускорений<e1> и <e2> (таблица 3).
3.Используя правила оценки погрешностей косвенных измерений, определите погрешности оценки момента инерции D Jс, взяв значения среднеквадратических отклонений из таблицы 3.
4.Запишите, используя правила округления, окончательный результат работы виде
Jc =<Jc> ± D Jс, в кг×м2
5. По формуле (20) рассчитайте момент инерции вращаемых грузов Jгр.
6.Используя правила оценки погрешностей косвенных измерений, определите погрешности оценки момента инерции DJг, взяв значения среднеквадратических отклонений из таблицы 3.
7.Запишите, используя правила округления, окончательный результат работы виде
Jгр =< Jгр > ± D Jгр, в кг×м2
8.Рассчитайте теоретическое значение момента инерции вращаемых грузов  по формуле (21).
по формуле (21).
9.Сформулируйте и запишите вывод, сравнив и проанализировав полученные результаты.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Сформулируйте основной закон динамики вращательного движения.
2.Что называется моментом инерции твердого тела?
3.Что называется моментом силы, и в каких единицах он измеряется?
4.Сформулируйте теорему Штейнера.
5. Рассчитайте момент инерции тела по указанию преподавателя.
6. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Ивлиев А.Д. Физика: Учебное пособие для вузов. СПб: Лань, 2008. 671 с.
Ивлиев А.Д. Физика. Квантовая механика. Физика атомов и молекул. Физика твердого тела. Физика атомного ядра и элементарных частиц: учеб. пособие для вузов. Екатеринбург : Издательство УГТУ-УПИ, 2005. 247 с.
Ивлиев А.Д. Классическая механика. Специальная теория относительности. Электричество и магнетизм. Колебания и волны. Молекулярная физика и термодинамика: учеб. пособие для вузов. Екатеринбург : Издательство УГТУ-УПИ, 2004. 617 с.
Ивлиев А.Д. Физика: Классическая механика. Специальная теория относительности. Электричество и магнетизм. Колебания и волны. Молекулярная физика и термодинамика: учеб. пособие для вузов. Екатеринбург: Издательство УГТУ-УПИ, 2005. 617 с.
Арсентьев В. В [и др.] Курс физики. В 2 т. Т. 1: учебник для вузов. СПб. Лань, 2007. 572 с.
Приложение А
Форма отчета по лабораторной работе
ОТЧЕТ
по лабораторной работе № 3
Измерение момента инерции твердого тела
с помощью маятника Обербека
студент ______________
группа _______________
Дата ________________
Преподаватель _____________
РГППУ
1.Расчетные формулы.
Постоянная часть момента инерции маятника Обербека:
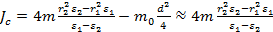 ,
,
где  – масса подвижного (вращаемого) груза,
– масса подвижного (вращаемого) груза,  – масса опускаемого груза,
– масса опускаемого груза,  и
и  – положения грузов относительно оси маятника,
– положения грузов относительно оси маятника,  и
и  – угловые ускорения шкива маятника, d – диаметр шкива.
– угловые ускорения шкива маятника, d – диаметр шкива.
Момент инерции подвижных грузов, находящихся на расстоянии  от оси вращения:
от оси вращения:

Теоретическая оценка момента инерции грузов, находящихся на расстоянии  :
:

2.Средства измерений и характеристики установки.
Таблица 1.Средства измерений
| Средство измерения, его тип и номер | Цена деления шкалы | Предел измерения | Предел основной погрешности |
| Линейка 1 (фиксированная) | |||
| Линейка 2* |
* - при выполнении работы без компьютера.
Таблица 2.Характеристики установки
| Масса вращаемого груза | Масса опускаемого груза | Диаметр шкива | Расстояние до центра масс вращаемых грузов | |
| m, г | m0, г | d, мм | r1, мм | r2, мм |
| 55,0 | 200,0 | |||
| Систематическая погрешность | ||||
| qm, г | qm0, г | qd, мм | qr1, мм | qr2, мм |
| 0,5 | 5,0 | 0,5 | 0,5 | 0,5 |
3.Результаты измерений и математическая обработка результатов измерений.
Таблица 3. Определение углового ускорения шкива маятника
| Положение грузов | Угловое ускорение ei | Номер опыта | <ei> | S<ei> | ||||
| r1= | e1, с-2 | |||||||
| r2= | e2, с-2 | |||||||
| отсутствуют | e3, с-2 |
Средние значения моментов инерции:
 =........... кг×м2 ,
=........... кг×м2 ,
 =........... кг×м2 ,
=........... кг×м2 ,
· Расчет случайной погрешности 
 = ........... кг×м2 ,
= ........... кг×м2 ,
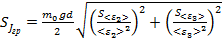 = ........... кг×м2 ,
= ........... кг×м2 ,
 ........... кг×м2,
........... кг×м2,
 ........... кг×м2,
........... кг×м2,
 для числа измерений n=5 при доверительной вероятности p=0,95.
для числа измерений n=5 при доверительной вероятности p=0,95.
· Расчет систематической погрешности 
 ........... кг×м2,
........... кг×м2,
 ........... кг×м2,
........... кг×м2,
где 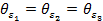 =0,01 с-2.
=0,01 с-2.
Расчет абсолютной погрешности 
 =.......... кг×м2,
=.......... кг×м2,
 =.......... кг×м2,
=.......... кг×м2,
· Запись окончательного результата
 =
= 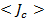 ±
± 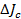 = ........... кг×м2,
= ........... кг×м2,
 =
=  ±
±  = ........... кг×м2, при доверительной вероятности р=0,95.
= ........... кг×м2, при доверительной вероятности р=0,95.
· Расчет теоретического значения.
 =........... кг×м2.
=........... кг×м2.
4.Вывод:
Дата добавления: 2015-01-29; просмотров: 1207; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Равноапостольная царица Елена | | | для выполнения лабораторной работы 2 |