
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерференция света в тонких пленках
Различные цвета тонких пленок — результат интерференции двух волн, отражающихся от нижней и верхней поверхностей пленки. При отражении от верхней поверхности пленки происходит потеря полуволны. Следовательно, оптическая разность хода  .
.
Тогда условие максимального усиления интерферирующих лучей в отраженном свете следующее: 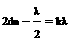 .
.
Если потерю полуволны не учитывать, то 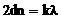 .
.
На практике чисто монохроматическая волна не осуществима, так как должна была бы быть бесконечной - прежде всего, во времени. Реальные процессы излучения ограничены во времени, и поэтому под монохроматической обычно понимается волна с очень узким спектром. Чем уже интервал, в котором находятся частоты реальной волны, тем «монохроматичнее» излучение.
В природе и технике наиболее близко к монохроматическому излучение отдельных линий спектров испускания свободныхатомов и молекул. Эти линии соответствуют переходу атома из состояния с большей энергией в состояние с меньшей, а частоты соответствующих монохромных волн равны разнице уровней энергии, поделённой на постоянную Планка.
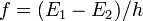
Для получения когерентных световых волн с помощью обычных (нелазерных) источников применяют метод разделения света от одного источника на две или нескольких систем волн (световых пучков). В каждой из них представлено излучение одних и тех же атомов источника, так что эти волны когерентны между собой и интерферируют при наложении. Разделение света на когерентные пучки можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.
Вопрос №24 Явление дифракции света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля на круглом отверстии и диске.
Дифракция света– это отклонение световых лучей от прямолинейного распространения при прохождении сквозь узкие щели, малые отверстия или при огибании малых препятствий.
Явление дифракции света доказывает, что свет обладает волновыми свойствами.
Для наблюдения дифракции можно:
- пропустить свет от источника через очень малое отверстие или расположить экран на большом расстоянии от отверстия. Тогда на экране наблюдается сложная картина из светлых и темных концентрических колец.
- или направить свет на тонкую проволоку, тогда на экране будут наблюдаться светлые и темные полосы, а в случае белого света-радужная полоса.
Принцип Гюйгенса – Френеля
Все вторичные источники, расположенные на поверхности фронта волны, когерентны между собой.
Амплитуда и фаза волны в любой точке пространства – это результат интерференции волн, излучаемых вторичными источниками.
Принцип Гюйгенса-Френеля дает объяснение явлению дифракции:
1. вторичные волны, исходя из точек одного и того же волнового фронта (волновой фронт – это множество точек, до которых дошло колебание в данный момент времени) , когерентны, т.к. все точки фронта колеблются с одной и той же частотой и в одной и той же фазе;
2. вторичные волны, являясь когерентными, интерферируют.
Явление дифракции накладывает ограничения на применение законов геометрической оптики:
Закон прямолинейного распространения света, законы отражения и преломления света выполняются достаточно точно только , если размеры препятствий много больше длины световой волны.
Дифракция накладывает предел на разрешающую способность оптических приборов:
- в микроскопе при наблюдении очень мелких предметов изображение получается размытым
- в телескопе при наблюдении звезд вместо изображения точки получаем систему светлых и темных полос. случае белого света – радужная полоса.
Зоны Френеля, участки, на которые можно разбить поверхность световой (или звуковой) волны для вычисления результатов дифракции света (или звука). Впервые этот метод применил О. Френель в 1815—19. Суть метода такова. Пусть от светящейся точки Q (рис.) распространяется сферическая волна и требуется определить характеристики волнового процесса, вызванного ею в точке Р. Разделим поверхность волны S на кольцевые зоны; для этого проведём из точки Р сферы радиусами PO, Pa = PO + l/2; Pb = Pa +l/2, Pc = Pb + l/2, (О — точка пересечения поверхности волны с линией PQ; l — длина световой волны). Кольцеобразные участки поверхности волны, "вырезаемые" из неё этими сферами, и называется З. Ф. Волновой процесс в точке Р можно рассматривать как результат сложения колебаний, вызываемых в этой точке каждой З. Ф. в отдельности. Амплитуда таких колебаний медленно убывает с возрастанием номера зоны (отсчитываемого от точки О), а фазы колебаний, вызываемых в Р смежными зонами, противоположны. Поэтому волны, приходящие в Р от двух смежных зон, гасят друг друга, а действие зон, следующих через одну, складывается. Если волна распространяется, не встречая препятствий, то, как показывает расчёт, её действие (сумма воздействий всех З. Ф.) эквивалентно действию половины первой зоны. Если же при помощи экрана с прозрачными концентрическими участками выделить части волны, соответствующие, например, N нечётным зонам Френеля, то действие всех выделенных зон сложится и амплитуда колебаний Uнечёт в точке Р возрастёт в 2N раз, а интенсивность света в 4N2 раз, причём освещённость в точках, окружающих Р, уменьшится. То же получится при выделении только чётных зон, но фаза суммарной волны Uчётбудет иметь противоположный знак.
Такие зонные экраны (т. н. линзы Френеля) находят применение не только в оптике, но и в акустике и радиотехнике — в области достаточно малых длин волн, когда размеры линз получаются не слишком большими (сантиметровые радиоволны, ультразвуковые волны).
Поставим между точечным источником  и точкой наблюдения
и точкой наблюдения 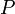 непрозрачный экран с круглым отверстием.
непрозрачный экран с круглым отверстием.
Согласно Френелю, действие такого препятствия сходится к тому, что экран как-бы устраняет часть волнового фронта.
Будем предпологать, кроме того, что размеры отверстия можно менять, что дает возможность открывать любое число зон Френеля.
Если открыть первую зону Френеля, то амплитуда и интенсивность света в той же точке будут 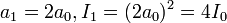 .
.
При удалении от центра 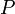 интенсивность будет монотонно убывать. При расширении отверстия в точку
интенсивность будет монотонно убывать. При расширении отверстия в точку 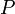 начнут проходить вторичные волны. Их интерференция с ранее пришедшими волнами вызовет уменьшение интенсивности в той же точке. Когда отверстие откроет две первые зоны Френеля, то их действия в точке
начнут проходить вторичные волны. Их интерференция с ранее пришедшими волнами вызовет уменьшение интенсивности в той же точке. Когда отверстие откроет две первые зоны Френеля, то их действия в точке 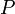 практически полностью уничтожат друг-друга из-за интерференции. В точке
практически полностью уничтожат друг-друга из-за интерференции. В точке 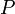 получиться темный кружок , окруженный светлым кольцом.
получиться темный кружок , окруженный светлым кольцом.
Вообще, при нечетном количестве открытых зон центр дифракционных колец светлый, при четном темный.
2. Определим теперь размеры и число 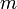 зон Френеля, укладывающихся в отверствии
зон Френеля, укладывающихся в отверствии  . Пусть
. Пусть 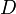 -диаметр отверствия, а
-диаметр отверствия, а  и
и  - расстояние от его центра до точек
- расстояние от его центра до точек 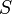 и
и 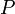 . Из точек
. Из точек 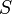 и
и 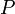 как из центров опишем сферы, проходящие через край отверстия
как из центров опишем сферы, проходящие через край отверстия  . Пренебрегая квадратами отрезков
. Пренебрегая квадратами отрезков  и
и 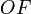 , по известной теореме можно написать:
, по известной теореме можно написать:

Отсюда
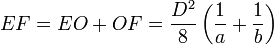
Число 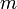 найдется делением этого отрезка на
найдется делением этого отрезка на  . Оно равно
. Оно равно
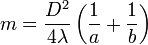
Если 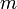 целое, то
целое, то 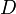 будет диаметром, a
будет диаметром, a  - радиусом
- радиусом 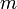 -ой, точнее ее внешнего края. Следовательно
-ой, точнее ее внешнего края. Следовательно

Вопрос № 25 Явление диф. света. Дифракция Фраунгофера на узкой щели.
Простейшим для расчета и практически очень важным случаем является фраунгоферова дифракция на длинной прямоугольной щели (Дифракция Фраунгофера на щели). Ширину щели обозначим через b, ее длину будем считать бесконечной. Пусть на щель нормально падает плоская монохроматическая волна. Световое поле за щелью найдется по принципу Гюйгенса как результат интерференции когерентных вторичных волн, исходящих из различных точек волнового фронта на щели. Вторичные волны, излучаемые полоской волнового фронта ширины dx, параллельной щели, складываясь, дают цилиндрическую волну, осью которой является эта полоска. Зависимость этой волны от направления ее распространения, определяемого углом j должен предполагаться малым. Однако необходимо учесть разности фаз между волнами, исходящими из различных полосок. Разумеется, речь идет о фазах колебаний на бесконечном расстоянии от щели. Волна, исходящая из dx под углом j, опережает по фазе волну того же направления, исходящую из середины щели О, на kx sinj.
Поэтому результирующее поле в бесконечности, создаваемое всей щелью, представиться интегралом
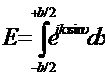
Здесь опущены все множители, не являющиеся на относительное распределение волнового поля по направлениям. Вычислив интеграл, получим

Где введено обозначение
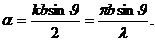
Отсюда для распределения интенсивности света по направлениям найдем 
Где  - интенсивность в направлении падающей волны. Обе функции обращаются в максимум, равной единице, при a=0. При
- интенсивность в направлении падающей волны. Обе функции обращаются в максимум, равной единице, при a=0. При 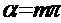 , где m=1,2 они равны 0. Между двумя соседними минимумами располагаются максимумы различных порядков. Их положения определяются трансцендентным уравнением a cos-sina=0. Практически можно считать, что максимумы располагаются посередине между соседними минимумами.
, где m=1,2 они равны 0. Между двумя соседними минимумами располагаются максимумы различных порядков. Их положения определяются трансцендентным уравнением a cos-sina=0. Практически можно считать, что максимумы располагаются посередине между соседними минимумами.
Вопрос №26. Дифракция Фраунгофера на дифракционной решетке. Дифракционные спектры. Угловая дисперсия и разрешающая способность дифракционной решетки.
Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка  , что сильно упрощает теоретическое рассмотрение явления. Здесь
, что сильно упрощает теоретическое рассмотрение явления. Здесь 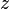 — расстояние от отверстия или преграды до плоскости наблюдения,
— расстояние от отверстия или преграды до плоскости наблюдения, 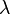 — длина волны излучения, а
— длина волны излучения, а  — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля
— радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля 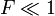 , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.
, при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.
Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).
Дифракция Френеля:
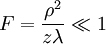 Дифракция Фраунгофера:
Дифракция Фраунгофера:
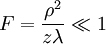
Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Рассматривая дифракцию Фраунгофера на щели, мы видели, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.
Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.
Рассмотрим дифракционную решетку. На рис. 262 для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d=a+b называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления j одинаковы в пределах всей дифракционной решетки:
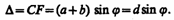 (180.1)
(180.1)
Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (179.2):
 (180.2)
(180.2)
Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т. е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей l/2, 3l/2, ..., посылаемых, например, от крайних левых точек М и С обеих щелей. Таким образом, с учетом (180.1) условие дополнительных минимумов:
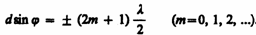
Наоборот, действие одной щели будет усиливать действие другой, если
 (180.3)
(180.3)
т. е. выражение (180.3) задает условиеглавных максимумов.
Таким образом, полная дифракционная картина, для двух щелей определяется из условий:

т. е. между двумя главными максимумами располагается один дополнительный минимум. Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагается два дополнительных минимума, при четырех щелях — три и т. д.
Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (180.2), условием главных максимумов — условие (180.3), а условием дополнительных минимумов
 (180.4)где т' может принимать все целочисленные значения, кроме 0, N, 2N, .... т. е. кроме тех, при которых условие (180.4) переходит в (180.3). Следовательно, вслучае N щелей между двумя главными максимумами располагается N–1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон. Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На рис. 263 качественно представлена дифракционная картина от восьми щелей. Так как модуль sin j не может быть больше единицы, то из (180.3) следует, что число главных максимумов
(180.4)где т' может принимать все целочисленные значения, кроме 0, N, 2N, .... т. е. кроме тех, при которых условие (180.4) переходит в (180.3). Следовательно, вслучае N щелей между двумя главными максимумами располагается N–1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон. Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На рис. 263 качественно представлена дифракционная картина от восьми щелей. Так как модуль sin j не может быть больше единицы, то из (180.3) следует, что число главных максимумов
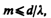
т. е. определяется отношением периода решетки к длине волны. Положение главных максимумов зависит от длины волны l (см. (180.3)). Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (т=0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная — наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т. е. дифракционная решетка может быть использована как спектральный прибор. Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем штрихов и их частотой (от 6000 до 0,25 штрих/мм, что позволяет перекрывать область спектра от ультрафиолетовой его части до инфракрасной). Например, ступенчатый профиль решетки позволяет концентрировать основную часть падающей энергии в направлении одного определенного ненулевого порядка.
Вопрос №27 Явление поляризации света. Естественный и поляризационный свет. Виды поляризации. Закон Малюса.
1. Свет, испускаемый обычными источниками излучения, представляет собой множество квантов, каждом из которых электрический вектор направлен в произвольном направлении, перпендикулярном направлению распространения луча. Такой свет называется естественным или неполяризованным.
1.
Если в пучке света имеется преимущественное направление колебаний электрического вектора, такой свет называется частично поляризованным.
2.
Поляризацией называется выделение линейно поляризованного света из естественного или частично поляризованного света.
3.
Устройства, позволяющие выделять линейно поляризованный свет из естественного или частично поляризованного света, называются поляризаторами. Их действие основано на поляризации света при его отражении или преломлении на границе раздела двух сред.
4.
Эти же устройства можно использовать в качестве анализаторов – устройств, позволяющих определить характер и степень поляризации.
5.
Степенью поляризации называется величина
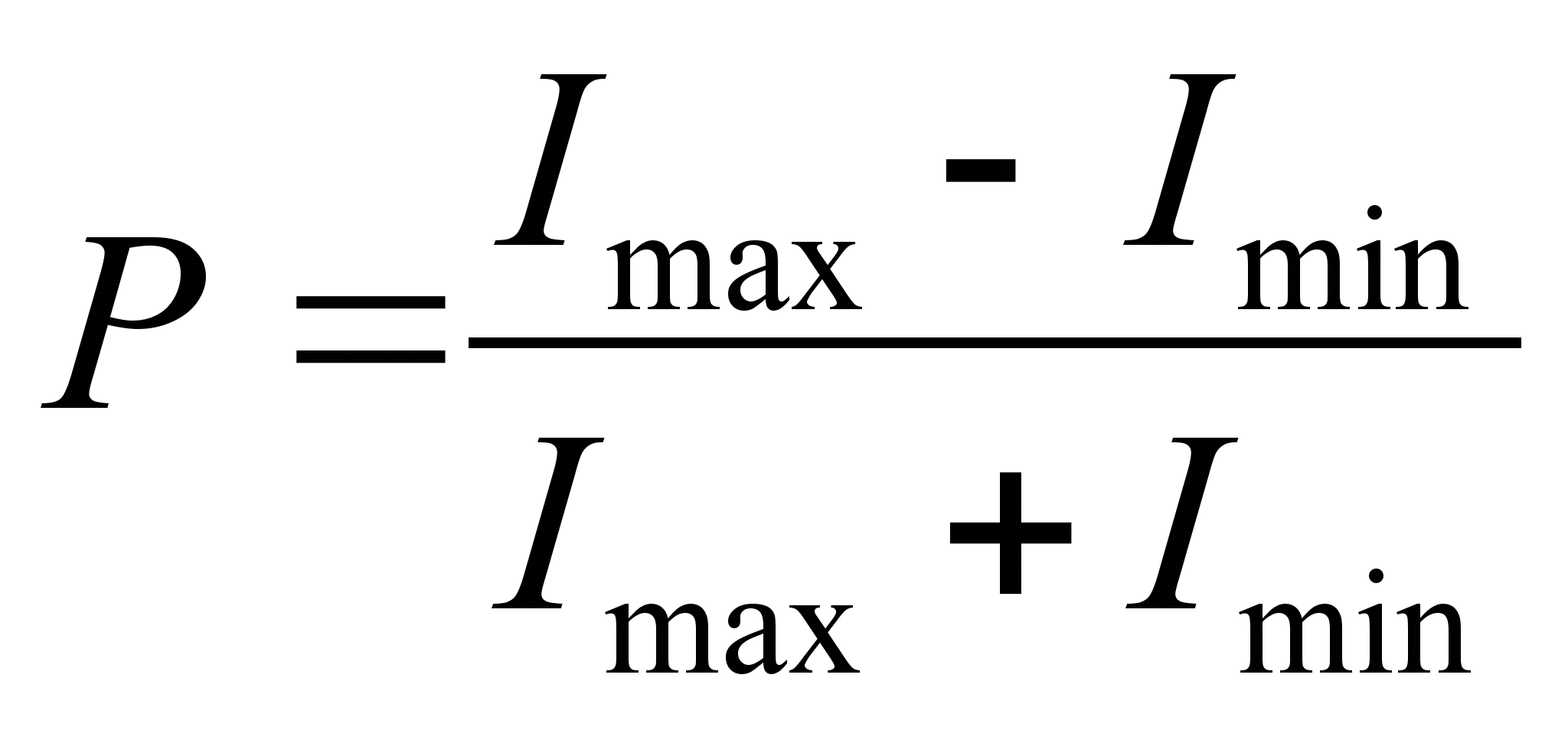
где Imax и Imin – соответственно максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.
2.
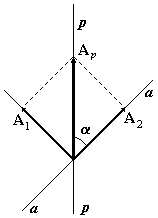
Если на поляризатор перпендикулярно его плоскости падает линейно поляризованный свет, электрический вектор которого направлен вдоль линии р-р, то падающий свет можно представить в виде двух волн, линейно поляризованных в двух взаимно перпендикулярных плоскостях. Поляризатор пропускает свет, электрический вектор которого направлен вдоль линии а-а, и не пропускает свет, электрический вектор которого направлен в перпендикулярном направлении.
1.
Амплитуда света, выходящего из поляризатора, равна
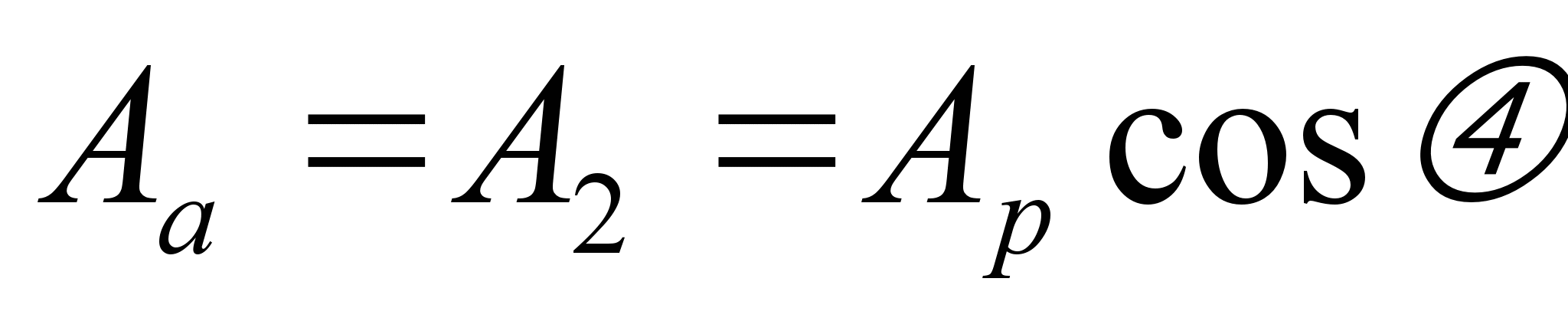
Соответственно интенсивности линейно поляризованного света Ia и падающего на поляризатор света Ipсвязаны между собой уравнением
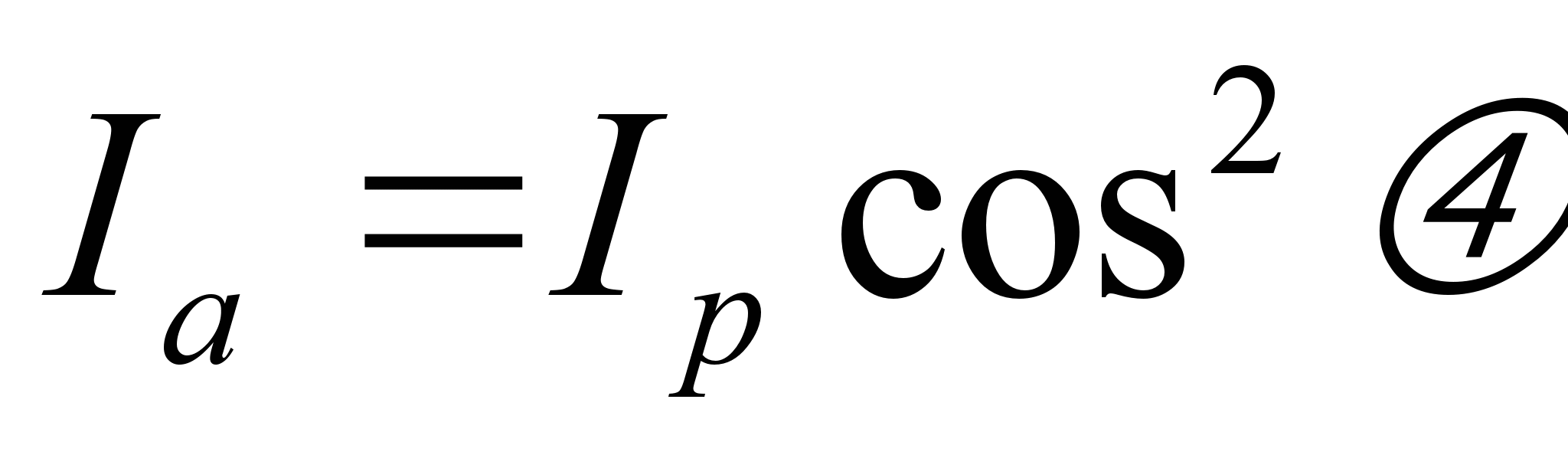 (закон Малюса)
(закон Малюса)
1.
Плоскость поляризации света (плоскость колебаний электрического вектора), пропускаемого поляризатором, называется главной плоскостью поляризации.
2.
При изучении закономерностей поляризации естественного света при отражении и преломлении от поверхности раздела двух сред этот свет удобно рассматривать как совокупность двух линейно поляризованных волн – s- и р-типа.
1.
В волне р-типа вектор Ер лежит в плоскости падения, а в волне s-типа вектор Еs лежит перпендикулярно плоскости падения.
2.
Коэффициент отражения волн s-типа всегда больше коэффициента отражения волн р-типа, а потому отраженный и преломленный лучи частично поляризованы – в отраженном луче преобладают волна s-типа, а в преломленном луче - р-типа.
3.
Отраженный свет полностью линейно поляризован при угле падения iБр (угол Брюстера), удовлетворяющем условию
tg iБр = n12 (закон Брюстера)
где n12 – относительный показатель преломления среды, отражающей свет.
4.

Если i = iБр, то отраженный и преломленный лучи взаимно перпендикулярны и коэффициент отражения волны р-типа равен нулю, а отражается только волна s-типа. Однако, коэффициент отражения волны s-типа много меньше 1 (~ 0,15), а потому проходящий свет поляризован лишь частично.
5.
Степень поляризации проходящего луча можно увеличить, пропуская луч через стопку параллельных прозрачных пластин, установленных под углом Брюстера к падающему лучу. Если в стопке пластин поглощения не происходит, то интенсивности лучей отраженного Is и проходящего Ip линейно поляризованного света равны половине интенсивности падающего естественного света

1.
Согласно представлениям классической электронной теории образование отраженной волны обусловлено вторичными волнами, которые излучают молекулы осцилляторы среды, отражающей свет.
1.
Волне s-типа соответствуют осцилляторы, оси которых перпендикулярныплоскости падения.
2.
Волне р-типа соответствуют осцилляторы, оси которых лежат в плоскостипадения и перпендикулярны направлению преломленного луча.
3.
Так как осцилляторы не могут излучать в направлении оси диполя, то при угле i = iБротраженный луч перпендикулярен преломленному лучу и, следовательно, оси диполя осцилляторов, генерирующих волны р-типа, будут параллельны отраженному лучу. По этой причине в отраженном луче при i = iБр нет волн р-типа (полностью поляризованный луч).
2.
Большинство кристаллов оптически анизотропно – их относительная диэлектрическая проницаемость и показатель преломления зависят от направления электрического вектора Есветовой волны. Это приводит к возникновению явления, называемого двойным лучепреломлением.
1. При двойном лучепреломлении луч, падающий на поверхность кристалла, раздваивается в нем на два преломленных луча.
1.
Направление в оптически анизотропном кристалле, вдоль которого свет распространяется, не испытывая двойного лучепреломления, называется оптической осью кристалла.
2. Оптически анизотропные кристаллы в зависимости от симметрии бывают однооснымиили двуосными.
3. Плоскость, содержащая оптическую ось и пересекающий ее луч, называется главной плоскостью или главным сечение одноосного кристалла.
4. В одноосном кристалле один из лучей о (обыкновенный луч) подчиняется обычным законам преломления.
5. Второй луч е не лежит в плоскости падения и не подчиняется закону Снеллиуса (необыкновенный луч)
- при нормальном падении луча на поверхность пластинки угол преломления re зависит от ориентации оптической оси по отношению к поверхности пластинки;
re равен нулю только, если ось перпендикулярна поверхности пластинки, либо параллельна поверхности.
1. В двуосном кристалле оба луча ведут себя как необыкновенные.
2. Падающая на оптически анизотропный кристалл волна возбуждает две вторичные волны, которые распространяются в в кристалле по различным направлениям, - обыкновенная и необыкновенная.
1. В обыкновенной волне электрический вектор Е направлен перпендикулярно к главной плоскости кристалла.
2. Электрический вектор Е необыкновенной волны лежит в главной плоскости кристалла.
3. Обыкновенный и необыкновенный лучи показывают направления векторов Умова-Пойнтинга соответствующих волн в кристалле, то есть направления переноса энергии этими волнами.
3. Сколость переноса энергии волной в оптически анизотропном кристалле называется лучевой скоростью волны.
1.
В одноосном кристалле скорость обыкновенного луча vо численно одинакова по всем направлениям

где no – показатель преломления для обыкновенного луча.
2.
Скорость необыкновенного луча численно равна

где nе – показатель преломления для необыкновенного луча.
1.
Значение nе зависит от направления необыкновенного луча по отношению к оптической оси кристалла.
2. Лучевой поверхностью волны в кристалле называется геометрическое место концов вукторов лучевой скорости волны, проведенной из некоторой точки О кристалла во всевозможных направлениях.
1.
Лучевая поверхность обыкновенной волны представляет собой сферу, так как скорость распространения обычной волны в кристалле одинакова по всем направлениям.
2.
Лучевая поверхность необыкновенной волны представляет собой эллипсоид вращениявокруг оптической оси. Эллипсоид и сфера касаются друг друга в точках пересечения с оптической осью.
3.
Если nе ≥ no, то эллипсоид вписан в сферу, а кристалл называется оптически положительным.
4.
Если nе ≤ no, то эллипсоид описан вокруг сферы, а кристалл называется оптически отрицательным.
3.
Пример расчета направлений обыкновенного и необыкновенного лучей в оптически отрицательном кристалле.
2.
Поляризационные призмы и поляроиды (дом. задание)
3.
В оптически изотропных кристаллах может возникать анизотропия под действием внешних факторов (искуственная оптическая анизотропия):
1.
При возникновении оптической анизотропии под действием внешнего давления – растяжения или сжатия – (фотоупругость) разность показателей преломления обыкновенного и необыкновенного лучей, при падении света перпендикулярно оси приложения деформации, пропорциональна нормальному давлению σ
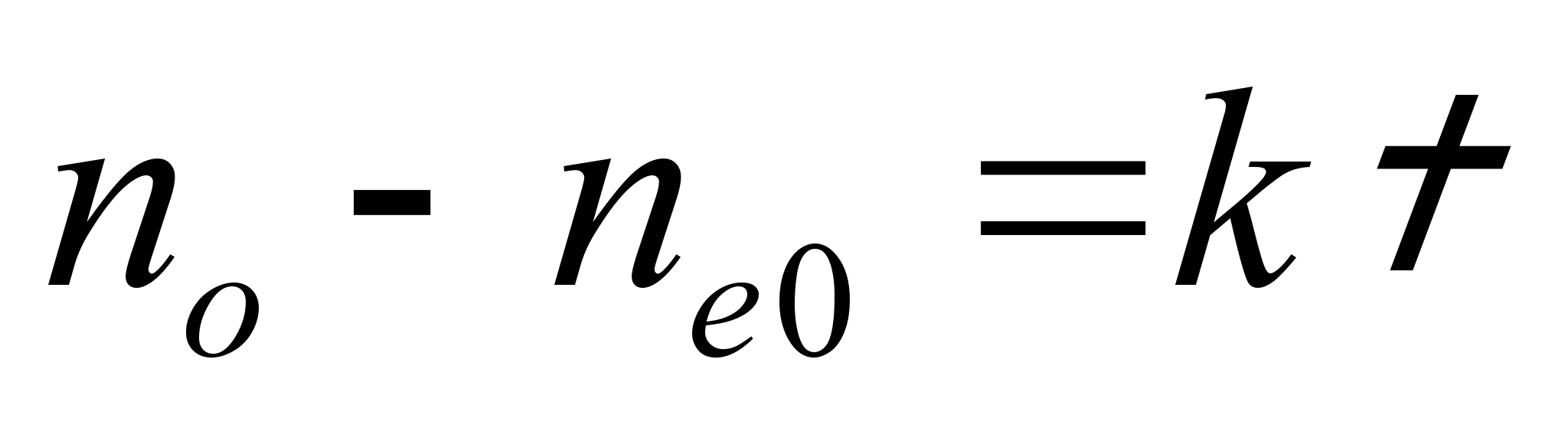
где k – коэффициент пропорциональности, зависящий от свойств вещества.
№28 Поляризация света на границе двух диэлектрических сред. Закон Брюстера. Стеклянная стопа.
Действие поляризаторов может быть основано на поляризации света при отражении и преломлении на границе раздела двух диэлектриков.
^ Оптически изотропная среда (т.е. среда, имеющая одинаковые оптические свойства во всех направлениях) представляет собой систему электрических зарядов – ионов и электронов, способных совершать вынужденные колебания под действием электромагнитных волн. Частота колебаний, соответствующая диапазону частот видимого света очень большая (порядка 1015 Гц). Поэтому только заряженные частицы очень маленькой массы могут следовать за изменением поля световой волны. Такими частицами являются электроны. Атомы и их ядра не могут следовать за изменением этого поля в силу их большой инертной массы. При этом предполагается, что в веществе электроны связаны квазиупругими силами, т.е. являются колебательными системами, характеризующимися часто простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь (рис. 4.4 а). Под действием электромагнитной волны электроны вещества совершают вынужденные колебания, излучая вторичные электромагнитные волны той же частоты, что и частота падающего света. Если волна распространяется в изотропной среде, то волновой фронт будет сферическим (рис. 4.4 б). При этом интенсивность вторичных волн зависит от угла θ и поэтому различна в разных направлениях. Зависимость интенсивности от угла наглядно показано на диаграмме направленности диполя (рис. 4.4 в). На рис. 4.4.в видно, что в направлении линии АА' (оси осциллятора) происходит колебания электрона, поэтому интенсивность излучения в этом направлении отсутствует. Интенсивность излучения будет максимальна в направлении оси Х, перпендикулярном линии АА'.
Взаимодействие электронной оболочки атомов с электромагнитным полем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, излучают вторичные электромагнитные волны. Поскольку среднее расстояние между атомами в жидкостях и твердых телах мало по сравнению с длиной цуга волн (около 3м), то электронные оболочки большого числа атомов возбуждаются одним цугом волн. Поэтому вторичные волны оказываются когерентными как между собой, так и падающей световой волной. Эти волны взаимно интерферируют. Их интерференцией объясняются явления отражения и преломления света в веществе.
При падении естественного света на границу раздела двух диэлектриков (например, из воздух на стекло) часть его отражается, а часть преломляется (рис. 4.5). Отраженный и преломленный свет оказываются частично поляризоваными. В отраженном свете преобладают волны, у которых световой вектор Е колеблется в плоскости, перпендикулярной плоскости падения (на рис. 4.5 колебания вектора Е изображены точками), а в преломленном свете – в плоскости падения (на рис. 4.5 колебания вектора Е изображены стрелками).
Степень поляризации как отраженного, так и преломленного света зависит от угла падения лучей и показателей преломления сред. Шотландский физик Дэвид Брюстер исследуя поляризацию света, установил (1815 г.) связь между относительным показателем преломления диэлектрика и углом падения света, при котором отраженный от поверхности свет полностью поляризован. Согласно закону Брюстерапри угле падения iБ (угол Брюстера), определяемого соотношением
tg iБ = n21
отраженный луч будет полностью плоскополяризован а преломленный луч – частично с максимальной степенью поляризации (рис. 4.6). Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны (это условие вытекает из закона Брюстера).
Степень поляризации преломленного света можно значительно повысить, пропуская свет через устройство, называемое стопой Столетова (рис. 4.7). Стопа Столетова представляет собой совокупность одинаковых параллельных друг другу пластинок из прозрачного диэлектрика (например, стекла). При многократном отражении и преломлении на каждой границе степень поляризации вырастает и на выходе из стопы свет становится полностью поляризованным.
Закон Брюстера можно пояснить, основываясь на диаграмме направленности излучения электрического диполя (осциллятора). Представим падающий естественный свет как результат сложения двух взаимно перпендикулярных колебаний (рис. 4.8). Один световой вектор (обозначим его Е||) будет колебаться в плоскости падения (на рис. 4.8 вектор Е|| показан стрелками), а другой (обозначим его Е^) будет колебаться в плоскости, перпендикулярной плоскости падения (на рис. 4.8 вектор Е^ показан точками).
При прохождении света через вещество под действием вектора Е|| электроны вещества будут совершать вынужденные колебания в плоскости падения (эти осцилляторы, оси которых лежат в плоскости падения, на преломленном луче обозначены стрелками), излучая при этом вторичные сферические волны в плоскости падения. Интенсивность таких волн будет максимальна в перпендикулярном направлении (это показано диаграммой направленности диполя на преломленном луче). Световому вектору Е^ будут соответствовать осцилляторы, оси которых лежат в перпендикулярной плоскости (на преломленном луче они обозначены точками). В направлении колебаний электронов излучения вторичных волн не происходит. При угле падения i = iБ отраженный луч перпендикулярен преломленному лучу и, следовательно, параллелен осцилляторам, оси которых расположены в плоскости падения. Данные осцилляторы не излучают в направлении отраженного луча и вклад в отраженную волну не дают. Отсюда следует, что в отраженном луче будет присутствовать только колебания Е^ и отраженный луч будет полностью поляризован.
Эффект поляризации отраженного света используется, например, для обнаружения с воздуха пленок нефти на поверхности моря.той собственных колебаний.
№ 29 Явление двойного лучепреломления. Поляризация призмы. Дихроизм поглощения света. Поляроиды. Закон Малюса.
Действие ряда поляризаторов основано на поляризации света при прохождении его через оптически анизотропные среды (т.е. среды, имеющие различные оптические свойства в различных направлениях). Все прозрачные кристаллы оптически анизотропны. Исключением являются кристаллы, имеющие кубическую кристаллическую решетку (например, соль NaCl). При прохождении света через оптически анизотропные кристаллы наблюдается явление двойного лучепреломления, которое состоит в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся с различными скоростями и в различных направлениях. В зависимости от типа симметрии оптически анизотропные кристаллы бывают одноосные либо двуосные,т.е. имеют одну или две оптические оси. Оптической осью называется такое направление в кристалле, вдоль которого распространяющийся свет не испытывает двойного лучепреломления. Важно отметить, что любая прямая параллельная данному направлению, также является оптической осью кристалла. Примером одноосного кристалла (рис. 4.9) является исландский шпат (диагональ кристалла ОО' совпадает с оптической осью), а также кварц, турмалин, апатит и другие. К двуосным кристаллам относятся гипс, слюда, топаз.
В 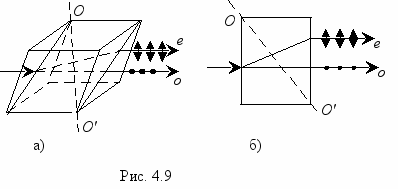 одноосных кристаллах (рис. 4.9 а) один из преломленных лучей, образующихся при двойном лучепреломлении, лежит в плоскости падения и подчиняется закону преломления, поэтому его назвали обыкновенным лучом и обозначают буквой "о". Скорость обыкновенного луча υочисленно одинакова по всем направлениям:υо = c/nо, где nо = const- показатель преломления кристалла для обыкновенного луча. Второй луч называют необыкновенным и обозначают буквой "е". Он не лежит в плоскости падения и не подчиняется закону преломления. Соответственно скорость необыкновенного луча υе = c/nе, где nе - показатель преломления кристалла для необыкновенного луча. Значения nе и υе зависят от направления распространения необыкновенного луча по отношению к оптической оси кристалла. Для луча, распространяющегося вдоль оптической оси показатели преломления обыкновенного и необыкновенного лучей равны nе = nо и υе = υо. Значение nе наиболее сильно отличается от nо для направления, перпендикулярного оптической оси. Все эти различия между обыкновенным и необыкновенным лучами имеют место только внутри кристалла. На выходе из кристалла оба луча распространяются с одинаковой скоростью. В двуосных кристаллах оба преломленных луча ведут себя как необыкновенные.
одноосных кристаллах (рис. 4.9 а) один из преломленных лучей, образующихся при двойном лучепреломлении, лежит в плоскости падения и подчиняется закону преломления, поэтому его назвали обыкновенным лучом и обозначают буквой "о". Скорость обыкновенного луча υочисленно одинакова по всем направлениям:υо = c/nо, где nо = const- показатель преломления кристалла для обыкновенного луча. Второй луч называют необыкновенным и обозначают буквой "е". Он не лежит в плоскости падения и не подчиняется закону преломления. Соответственно скорость необыкновенного луча υе = c/nе, где nе - показатель преломления кристалла для необыкновенного луча. Значения nе и υе зависят от направления распространения необыкновенного луча по отношению к оптической оси кристалла. Для луча, распространяющегося вдоль оптической оси показатели преломления обыкновенного и необыкновенного лучей равны nе = nо и υе = υо. Значение nе наиболее сильно отличается от nо для направления, перпендикулярного оптической оси. Все эти различия между обыкновенным и необыкновенным лучами имеют место только внутри кристалла. На выходе из кристалла оба луча распространяются с одинаковой скоростью. В двуосных кристаллах оба преломленных луча ведут себя как необыкновенные.
Исследование обыкновенного и необыкновенного лучей показывает, что оба луча на выходе из кристалла полностью поляризованы. Вектор Е обыкновенного луча колеблется перпендикулярно главной плоскости (на рис. 4.9 эти колебания обозначены точками), а вектор Е необыкновенного луча колеблется в главной плоскости (на рис. 4.9 эти колебания показаны стрелками). Главной плоскостью или главным сечениемодноосного кристалла называется плоскость, проходящая через падающий луч и пересекающую его оптическую ось (рис. 4.9 б).
Двойное лучепреломление объясняется тем, что в кристаллах диэлектрическая проницаемость ε оказывается зависящей от направления. Для одноосных кристаллов диэлектрическая проницаемость в направлении оптической оси и диэлектрическая проницаемость в направлении, перпендикулярном к ней, имеют различные значения. Поскольку абсолютный показатель преломления  , а для большинства кристаллов магнитная проницаемость µ ≈ 1, то
, а для большинства кристаллов магнитная проницаемость µ ≈ 1, то 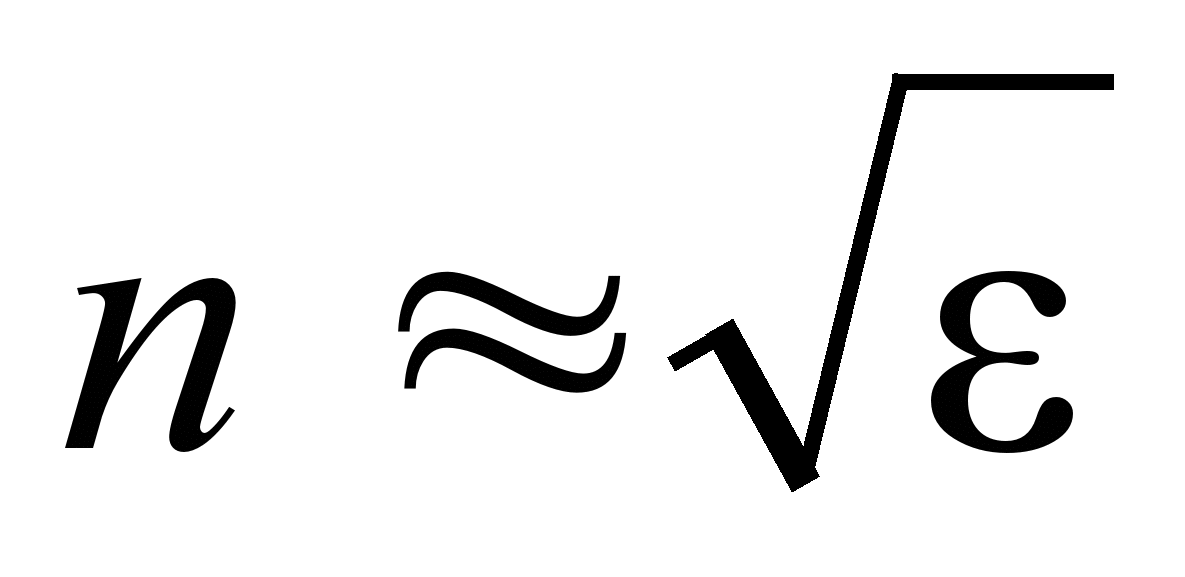 . Следовательно, из анизотропии диэлектрической проницаемости εвытекает анизотропия показателя преломления n.
. Следовательно, из анизотропии диэлектрической проницаемости εвытекает анизотропия показателя преломления n.
Допустим, что в точке S (рис. 4.10) внутри одноосного кристалла находится точечный источник света. На рис. 4.10 показано распространение обыкновенного и необыкновенного лучей в кристалле. Главная плоскость совпадает с плоскостью чертежа, прямая ОО' – оптическая ось. Волновая поверхность обыкновенного луча является сферой (т.к. nо = const и υо = c/nо = =const), необыкновенного луча – эллипсоид вращения (т.к.
nе ≠ const и υе = c/nо ≠ const). На рис. 4.10 хорошо видно, что наибольшее расхождение волновых поверхностных обыкновенного и необыкновенного лучей наблюдается в направлении, перпендикулярном оптической оси. Сфера и эллипсоид касаются друг друга в точках их пересечениях с оптической осью ОО'.Если υе< υо (nе>nо), то эллипсоид вписан в сферу (рис. 4.10 а), такой одноосный кристалл называетсяоптически положительным (например, кварц). Если υе> υо (nе<nо), то эллипсоид описан вокруг сферы (рис. 4.10 б), такой одноосный кристалл называется оптически отрицательным (например, исландский шпат, турмалин, апатит).
Некоторые кристаллы способны по-разному поглощать о- и е-лучи. Зависимость показателя поглощения среды от ориентации электрического вектора световой волны и от направления распространения света в кристалле называется дихроизмом, а сами
кристаллы – дихроичными. Примером дихроичного кристалла является турмалин. При толщине
в 1 мм пластинка турмалина полностью поглощает о-лучи и свет, прошедший сквозь нее, оказывается полностью поляризованным. Дихроичные пластинки могут применяться какполяризаторы света. Еще более ярко выращенным дихроичным свойством обладают кристаллы герапатита (сернокислого йод-хинина).
ПОЛЯРОИДЫ, прозрачные пленки (полимерные, монокристаллические и др.), преобразующие неполяризованный свет в линейно поляризованный, т.к. пропускают свет только одного направления поляризации. Это свойство широко используется для ослабления интенсивности света в солнцезащитных очках переменной плотности, в автомобильных фарах, в фотографии для устранения бликов и т.п. Поляроиды изобретены американским ученым Э. Лэндом в 1932.
№30 Явление вращения плоскости поляризации света. Оптическая активность. Эффект Фарадея. Поляриметры. Некоторые вещества (например, из твердых тел — кварц, сахар, киноварь, из жидкостей — водный раствор сахара, винная кислота, скипидар), называемыеоптически активными, обладают способностью вращать плоскость поляризации.Вращение плоскости поляризации можно наблюдать на следующем опыте (рис. 285). Если между скрещенными поляризатором Р и анализатором А, дающими темное поле зрения, поместить оптически активное вещество (например, кювету с раствором сахара), то поле зрения анализатора просветляется. При повороте анализатора на некоторый угол j можно вновь получить темное поле зрения. Угол j и есть угол, на который оптически активное вещество поворачивает плоскость поляризации света, прошедшего через поляризатор. Так как поворотом анализатора можно получить темное поле зрения, то свет, прошедший через оптически активное вещество, является плоско поляризованным.Опыт показывает, что угол поворота плоскости поляризации для оптически активных кристаллов и чистых жидкостей

для оптически активных растворов
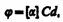 (196.1)
(196.1)
где d — расстояние, пройденное светом в оптически активном веществе, a([a]) — так называемое удельное вращение, численно равное углу поворота плоскости поляризации света слоем оптически активного вещества единичной толщины (единичной концентрации — для растворов), С — массовая концентрация оптически активного вещества в растворе, кг/м3. Удельное вращение зависит от природы вещества, температуры и длины волны света в вакууме.
Опыт показывает, что все вещества, оптически активные в жидком состоянии, обладают таким же свойством и в кристаллическом состоянии. Однако если вещества активны в кристаллическом состоянии, то не всегда активны в жидком (например, расплавленный кварц). Следовательно, оптическая активность обусловливается как строением молекул вещества (их асимметрией), так и особенностями расположения частиц в кристаллической решетке.
Оптически активные вещества в зависимости от направления вращения плоскости поляризации разделяются на право- и левовращающие. В первом случае плоскость поляризации, если смотреть навстречу лучу, вращается вправо (по часовой стрелке), во втором — влево (против часовой стрелки). Вращение плоскости поляризации объяснено О. Френелем (1817 г.). Согласно теории Френеля, скорость распространения света в оптически активных веществах различна для лучей, поляризованных по кругу вправо и влево.
Явление вращения плоскости поляризации и, в частности, формула (196.1) лежат в основе точного метода определения концентрации растворов оптически активных веществ, называемого поляриметрией (сахариметрией). Для этого используется установка, показанная на рис. 285. По найденному углу поворота плоскости поляризации j и известному значению [a] из (196.1) находится концентрация растворенного вещества.
Впоследствии М. Фарадеем было обнаружено вращение плоскости поляризации в оптически неактивных телах, возникающее под действием магнитного поля. Это явление получило название эффект Фарадея (или магнитного вращения плоскости поляризации). Оно имело огромное значение для науки, так как было первым явлением, в котором обнаружилась связь между оптическими и электромагнитными процессами.
Поляриметры-применяются в лабораториях пищевой, химической промышленности и других отраслях науки и производства для определения концентрации растворов оптически активных веществ, таких как сахар, глюкоза, белок, по углу вращения плоскости поляризации. Рекомендуется больным сахарным диабетом для индивидуального контроля содержания сахара в моче. Также позволяет наблюдать и измерить остаточные напряжения в стекле. Поскольку существует масса различных областей применения, то конструкции поляриметров могут отличаться, но ключевые элементы одинаковы.
· Источник света — чаще это натриевая лампа или лампа накаливания с тепловым экраном для защиты образца от ИК излучения (для твердых деталей важно избегать термических деформаций, для жидкостей — градиента плотности) и матовым стеклом, дающим равномерную засветку наблюдаемой области.
· Светофильтр — элемент, выделяющий определенную область в спектре, так как наблюдать приходится монохроматический свет. Таким элементом может быть пластина из фильтрующего вещества или призма.
· Двух поляризаторов расположенных по обе стороны от анализируемого образца. Часто один из них это поляроид, а второй либо поляроид, либо призма Николя.
· Пластин-компенсаторов толщиной кратной длине волны или четверть-волны, для подбора метода измерений.
· Измерительное устройство — лимб или электронный датчик.
№31 Явление дисперсии света. Дисперсионный спектр. Нормальная и аномальная дисперсия.
Диспе́рсия све́та (разложение света) — это явление зависимости абсолютного показателя преломления вещества от длины волны света. Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Причиной дисперсии является неодинаковая скорость распространения лучей света c различной длиной волны в оптической среде. Чем больше частота волны, тем больше показатель преломления и меньше ее скорость света в среде:
- у красного цвета максимальная скорость в среде и минимальная степень преломления;
- у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления;
- в вакууме скорости света разного цвета одинаковы.
Однако в некоторых веществах (например в парах йода) наблюдается эффект аномальной дисперсии, при котором синие лучи преломляются меньше, чем красные, а другие лучи поглощаются веществом и от наблюдения ускользают.
Дисперсия белого света указывает на его составную природу.
Белый свет разлагается на спектр и в результате прохождения через дифракционную решётку. Причем дифракционный и призматический спектры несколько отличаются: Призматический спектр сжат в красной части и растянут в фиолетовой (располагается в порядке убывания длины волны: от красного к фиолетовому). Нормальный (дифракционный) спектр равномерный во всех областях (располагается в порядке возрастания длин волн: от фиолетового к красному).
Дисперсия света дала своё название закону дисперсии, связывающему частоту и волновое число любого колебательного процесса, не обязательно электромагнитной волны.
Дисперсией объясняется факт появления радуги после дождя. Дисперсия является причиной хроматической аберрации— одного из тщательно устраняемых недостатков (аберраций) оптических систем, в том числе фотографических и видео-объективов.
Коши пришел к формуле, выражающей зависимость показателя преломления от длины волны n = a + b / L2 + c / L4 + ...
,где L - длина волны в вакууме, a,b,c, ... - постоянные, значения которых для каждого вещества должны быть определены в опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы Коши.
Благодаря дисперсии света, можно наблюдать цветовую "игру" на гранях бриллианта.
Следствием дисперсии является разложение света при прохождении его через призму на составляющие с различными длинами волн (монохроматические лучи). При разложении белого света, т.е света в видимом диапазоне, содержащего длины волн в диапазоне 380—760 нм, возникает радужная полоска (рис. 17.32), которую называют спектром. Впервые подробно исследовал дисперсию света И. Ньютон. Он доказал, что не призма окрашивает свет, а белыйсвет — сложный, он состоит из простых (монохроматических) лучей, которые при прохождении через призму отклоняются, но не разлагаются, и только в совокупности монохроматические лучи дают ощущение белого света.
Другой важный вывод, который сделал И. Ньютон: лучи различного цвета преломляются по-разному.
Таким образом, с помощью призмы, как и с помощью дифракционной решетки, можно получить спектр некоторого излучения. В дисперсионном и дифракционном спектрах имеются различия: 1) для дифракционного спектра можно создать равномерную шкалу по α. А так как функция n=f(λ) не линейная, то для дисперсионного спектра этого сделать нельзя, дисперсионный спектр не равномерный, он сжат в красной области и растянут в фиолетовой; 2) в дисперсионном спектре большее отклонение от первоначального направления испытывают фиолетовые лучи, в дифракционном — красные; 3) в дифракционном спектре наблюдается несколько порядков спектра, в дисперсионном — один.
№32 Тепловое излучение. Абсолютно-черное тело. Законы теплового излучения. Квантовая гипотеза Планка. Формула Планка для испускательной способности абсолютно-черного тела.
Все тела при температуре выше абсолютного нуля излучают электромагнитные волны. Этот кусок мела, я, вы, полы, тут всё излучает электромагнитные волны. Это излучение называется тепловым излучением. Механизм излучения простой: в конечном итоге все тела состоят из заряженных частиц, которые при температуре выше абсолютного нуля находятся в состоянии хаотического движения, а дёргающийся заряд излучает электромагнитные волны.2)
Дата добавления: 2015-01-29; просмотров: 501; Мы поможем в написании вашей работы!; Нарушение авторских прав |