
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Абсолютно чёрное тело
Тепловое излучение – следствие хаотического движения заряженных частиц, а оно происходит во всём диапазоне. Это означает, что длины волн при тепловом излучении меняются так:  . Понятно, что полная энергия как-то распределяется по длинам волн.1) Значит, если
. Понятно, что полная энергия как-то распределяется по длинам волн.1) Значит, если  это энергия, излучаемая в интервале
это энергия, излучаемая в интервале  , то мы можем написать
, то мы можем написать  . Очевидно, что на малых интервалах энергия линейна по интервалу, и она должна зависеть от длины волны. Тогда пишут:
. Очевидно, что на малых интервалах энергия линейна по интервалу, и она должна зависеть от длины волны. Тогда пишут:  , где функция
, где функция  называется спектральной плотностью излучения.2) Эта функция характеризует каждое тело. Любое тело имеет свои предпочтения: на одной длине волны излучает больше, на другой меньше, это зависит от его конкретного устройства.
называется спектральной плотностью излучения.2) Эта функция характеризует каждое тело. Любое тело имеет свои предпочтения: на одной длине волны излучает больше, на другой меньше, это зависит от его конкретного устройства.
Имеется другая важная характеристика – монохроматическая поглощательная способность, определяется так:  , это лучше переписать так:
, это лучше переписать так:  . Вот на этот стол падает энергия извне, часть этой энергии поглощается, а часть отражается, эта поглощательная способность определяет склонность тела к поглощению на данном интервале длин волн,
. Вот на этот стол падает энергия извне, часть этой энергии поглощается, а часть отражается, эта поглощательная способность определяет склонность тела к поглощению на данном интервале длин волн,  .
.
Для идеального зеркала, которое отражает всё падающее излучение на всех длинах волн,  . Наоборот, для тела, которое ничего не отражает ни при какой длине волны, но соответственно всё поглощает,
. Наоборот, для тела, которое ничего не отражает ни при какой длине волны, но соответственно всё поглощает,  . Значит,
. Значит,  определяет абсолютно чёрное тело, такие тела есть. Мы остановились на том, что абсолютно чёрное тело это тело, для которого
определяет абсолютно чёрное тело, такие тела есть. Мы остановились на том, что абсолютно чёрное тело это тело, для которого  на всех длинах волн, то есть оно поглощает всё падающее на него извне излучение и его не отражает. Мы видим определённые тела вследствие того, что мы видим отражённый от них свет, то есть мы видим отражённые электромагнитные волны,3) а если тело ничего не отражает, то, конечно, оно будет чёрным. Скажем, здесь сейчас кто-нибудь из вас стал бы абсолютно чёрным, как бы это воспринималось? А вот такой контур абсолютно чёрный без всяких деталей.4)Для света нет материальных объектов абсолютно прозрачных, а вот для нейтрино, например, практически всё абсолютно прозрачно.1)Есть природный объект, чёрная дыра, который является чёрным в этом смысле: всё, что на дыру падает извне, и вещество, и излучение, падает туда совершенно необратимо и безысходно.2) Но не надо таких экзотических объектов, чтобы реализовать абсолютно чёрное тело. Полость с маленькой дыркой даёт возможность реализовать абсолютно чёрное тело, а именно, вот эта поверхность дырки в полости ведёт себя как абсолютно чёрное тело по понятной причине: сюда заходит какое-то излучение, дальше оно испытывает там многократное отражение и выйдет обратно ничтожная часть того, что туда зашло, потому что при каждом взаимодействии со стенкой излучение поглощается. Окно в доме чёрное (без стекла, застеклённые окна отражают), если оно маленькое и помещение там большое. Так что абсолютно чёрное тело реализуемо.
на всех длинах волн, то есть оно поглощает всё падающее на него извне излучение и его не отражает. Мы видим определённые тела вследствие того, что мы видим отражённый от них свет, то есть мы видим отражённые электромагнитные волны,3) а если тело ничего не отражает, то, конечно, оно будет чёрным. Скажем, здесь сейчас кто-нибудь из вас стал бы абсолютно чёрным, как бы это воспринималось? А вот такой контур абсолютно чёрный без всяких деталей.4)Для света нет материальных объектов абсолютно прозрачных, а вот для нейтрино, например, практически всё абсолютно прозрачно.1)Есть природный объект, чёрная дыра, который является чёрным в этом смысле: всё, что на дыру падает извне, и вещество, и излучение, падает туда совершенно необратимо и безысходно.2) Но не надо таких экзотических объектов, чтобы реализовать абсолютно чёрное тело. Полость с маленькой дыркой даёт возможность реализовать абсолютно чёрное тело, а именно, вот эта поверхность дырки в полости ведёт себя как абсолютно чёрное тело по понятной причине: сюда заходит какое-то излучение, дальше оно испытывает там многократное отражение и выйдет обратно ничтожная часть того, что туда зашло, потому что при каждом взаимодействии со стенкой излучение поглощается. Окно в доме чёрное (без стекла, застеклённые окна отражают), если оно маленькое и помещение там большое. Так что абсолютно чёрное тело реализуемо.
Любое нагретое тело излучает электромагнитные волны. Чем выше температура тела, тем более короткие волны оно испускает. Тело, находящееся в термодинамическом равновесии со своим излучением, называют абсолютно черным (АЧТ). Излучение абсолютно черного тела зависит только от его температуры. В 1900 году Макс Планк вывел формулу, по которой при заданной температуре абсолютно черного тела можно рассчитать величину интенсивности его излучения.
Австрийскими физиками Стефаном и Больцманом был установлен закон, выражающий количественное соотношение между полной излучательной способностью и температурой черного тела:
|
Этот закон носит название закон Стефана–Больцмана. Константа σ = 5,67∙10–8 Вт/(м2∙К4) получила названиепостоянной Стефана–Больцмана.
Все планковские кривые имеют заметно выраженный максимум, приходящийся на длину волны
|
Этот закон получил название закон Вина. Так, для СолнцаТ0 = 5 800 К, и максимум приходится на длину волныλmax ≈ 500 нм, что соответствует зеленому цвету в оптическом диапазоне.
С увеличением температуры максимум излучения абсолютно черного тела сдвигается в коротковолновую часть спектра. Более горячая звезда излучает большую часть энергии в ультрафиолетовом диапазоне, менее горячая – в инфракрасном.
Согласно квантовой теории Планка, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями -- квантами, причем энергия ванта пропорциональна частоте колебания  , где
, где  -- постоянная Планка. Т.к. излучение испускается порциями, то энергия осциллятора (стоячей волны)
-- постоянная Планка. Т.к. излучение испускается порциями, то энергия осциллятора (стоячей волны)  может принимать лишь определенные дискретные значения, кратные целому числу эл-тарн порций энергии
может принимать лишь определенные дискретные значения, кратные целому числу эл-тарн порций энергии  :
:  (n=0,1,2,…). Ф-ла Планка (нахождение универсальной функции Кирхгофа):
(n=0,1,2,…). Ф-ла Планка (нахождение универсальной функции Кирхгофа): 
 , где
, где 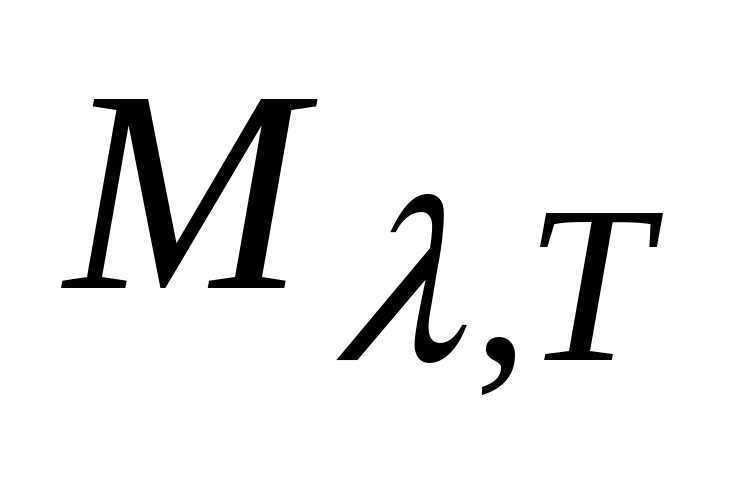 ,
,  -- спектральные плотности энергетической светимости ЧТ,
-- спектральные плотности энергетической светимости ЧТ, 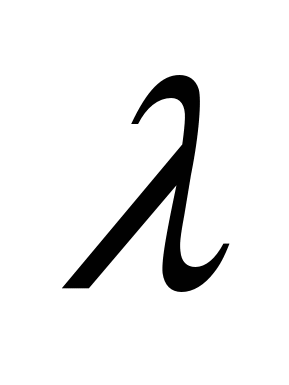 -- длина волны,
-- длина волны,  -- круговая частота, с – скорость света в вакууме, к – постоянная Больцмана, Т – термодинамическая температура, h – постоянная Планка,
-- круговая частота, с – скорость света в вакууме, к – постоянная Больцмана, Т – термодинамическая температура, h – постоянная Планка,  -- постоянная Планка, дел. на
-- постоянная Планка, дел. на  =
=  . Следствие: если
. Следствие: если 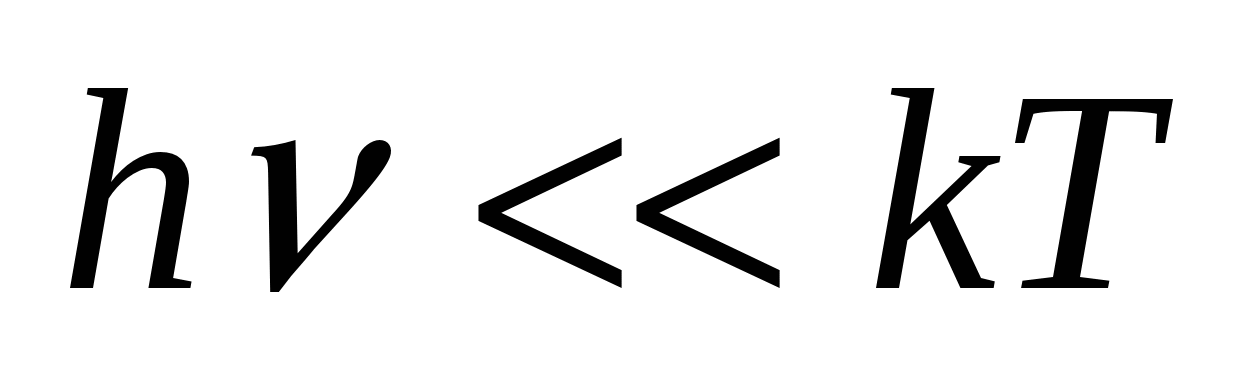 , то
, то 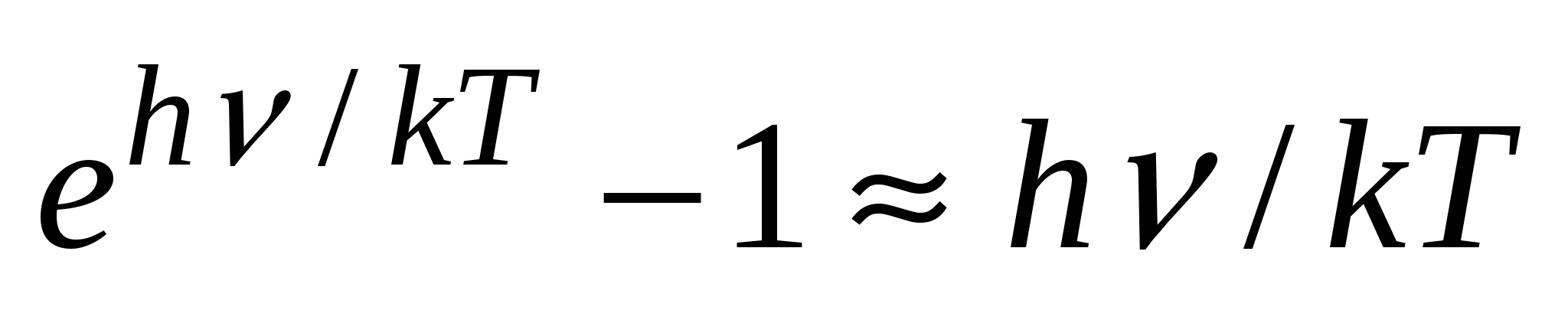 и из ф-лы Планка следует ф-ла Релея-Джинса:
и из ф-лы Планка следует ф-ла Релея-Джинса:  . В области больших частот
. В области больших частот  и единицей в знаменателе ф-лы можно пренебречь по сравнению с
и единицей в знаменателе ф-лы можно пренебречь по сравнению с  , тогда получим ф-лу
, тогда получим ф-лу 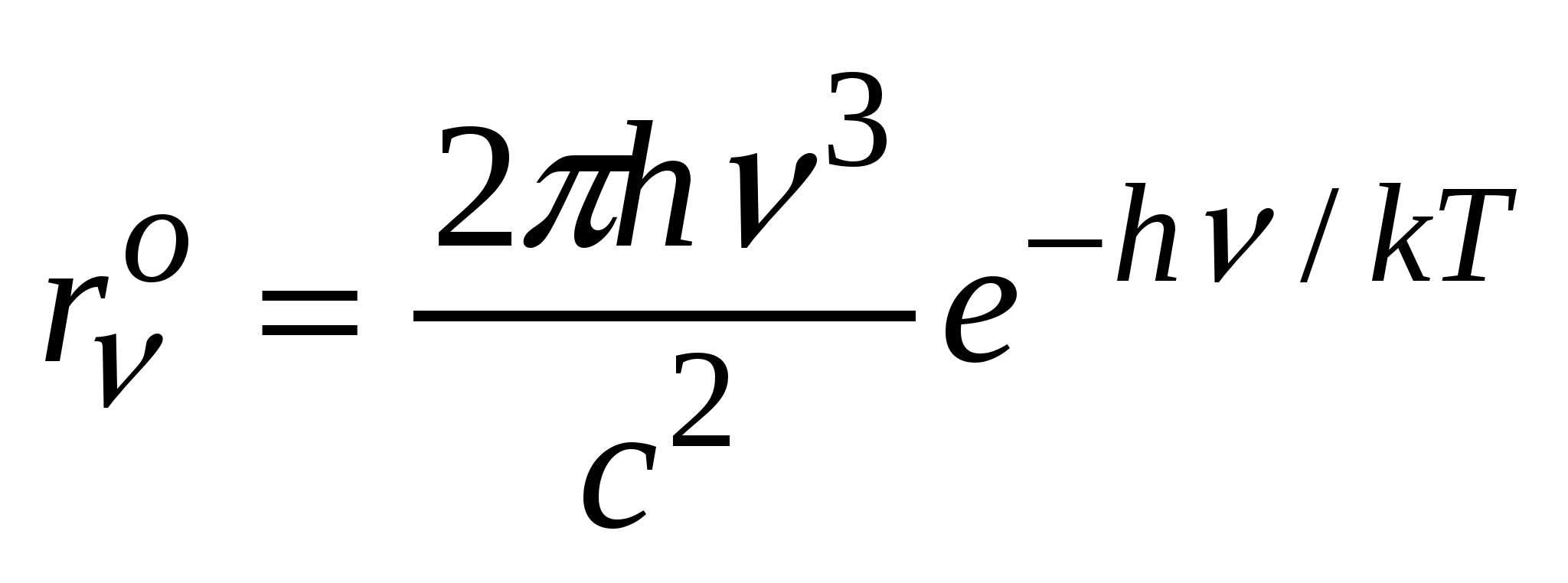 , эта ф-ла совпадает с ф-лой
, эта ф-ла совпадает с ф-лой  , причем а1=h/k
, причем а1=h/k
Испускательная и поглощательная способность.Спектральной хар-кой теплового излучения тела служит спектральная плотность энергетической светимости (испускательная способность), равная 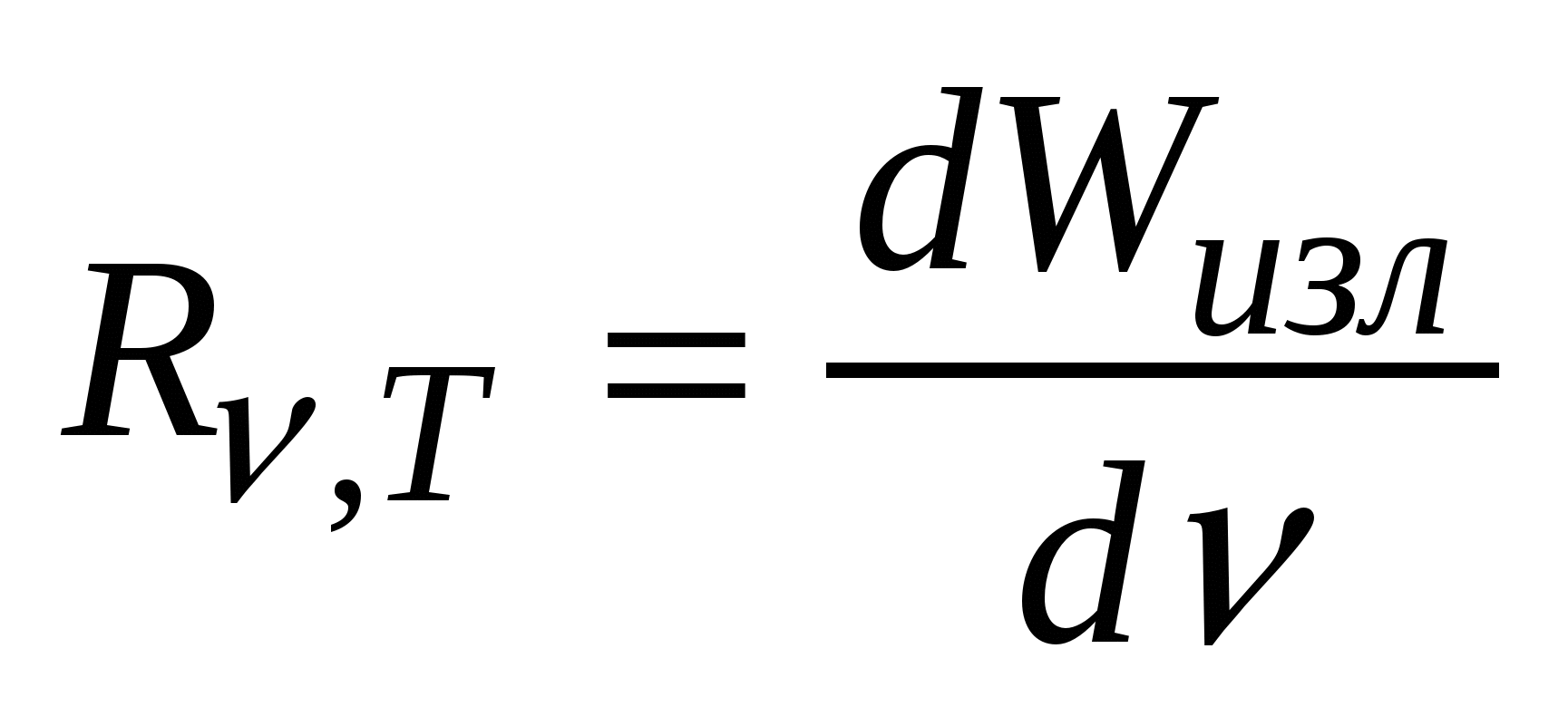 , где , где  -- энергия электромагнитного излучения, испускаемого за единицу времени с единицы площади поверхности тела в интервале частот от -- энергия электромагнитного излучения, испускаемого за единицу времени с единицы площади поверхности тела в интервале частот от  до до 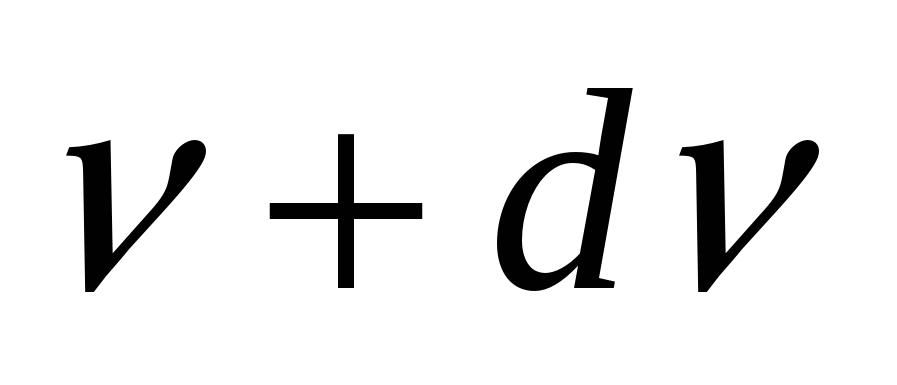 . Спектральная плотность энергетической светимости численно равна мощности излучения с единицы площади пов-ти этого тела в интервале частот единичной ширины. Единицей измерения является . Спектральная плотность энергетической светимости численно равна мощности излучения с единицы площади пов-ти этого тела в интервале частот единичной ширины. Единицей измерения является  Спектральной хар-кой поглощения электромагнитных волн телом служит спектральная поглощательная способность (поглощательная способность). Спектральной хар-кой поглощения электромагнитных волн телом служит спектральная поглощательная способность (поглощательная способность).  . Он показывает, какая доля энергии dW падающего на пов-ть тела эл. магн излучения с частотами от . Он показывает, какая доля энергии dW падающего на пов-ть тела эл. магн излучения с частотами от  до до 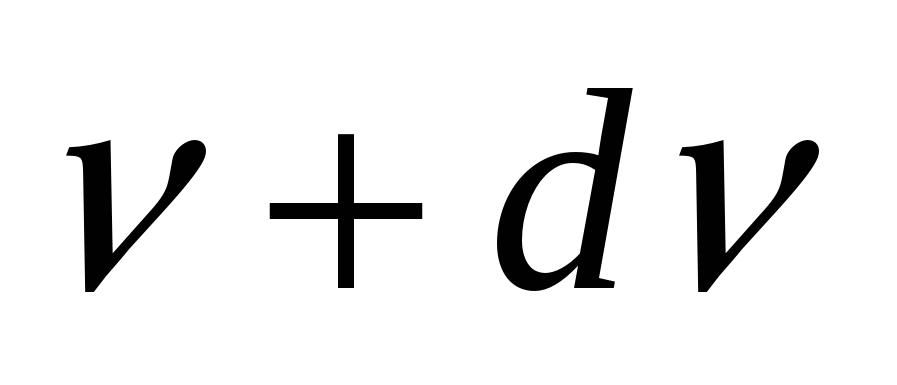 поглощается телом. Эта величина – безразмерная. поглощается телом. Эта величина – безразмерная.
|
№33 Внешний фотоэффект и его закономерности. Уравнения Энштейна для внешнего фотоэффекта. Энергия фотона. Вакуумный фотоэлемент.
Гипотеза Планка, решившая задачу теплового излучения черного тела, получила подтверждение и дальнейшее развитие при объяснении фотоэффекта – явление, открытие которого сыграло важную теорию в становлении квантовой теории. Различают фотоэффект внешний, внутренний и вентильный.Внешним фотоэффектомназывается испускание электронов в-вом под действием электромагнитного излучения (света). Он наблюдается в твердых телах (металлах, полупроводниках, диэлектриках), а так же в газах на отдельных атомах и молекулах. Внутренний фотоэффект – это вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. В р-тате концентрация носителей тока внутри тела увеличивается, что приводит к возникновению фотопроводимости (повышению электропроводности полупроводника или диэлектрика при его освещении) или возникновению ЭДС.Вентильный фотоэффект – возникновение ЭДС (фото-ЭДС) при освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля). При помощи вентильного фотоэффекта можно напрямую преобразовывать солнечную энергию в электрическую.
Уравнение Эйнштейна для внешнего фотоэффекта: Энергия падающего фотона расходуется на совершение работы выхода из металла и на сообщение фотоэлектрону кинетической энергии  . По закону сохранения энергии,
. По закону сохранения энергии, 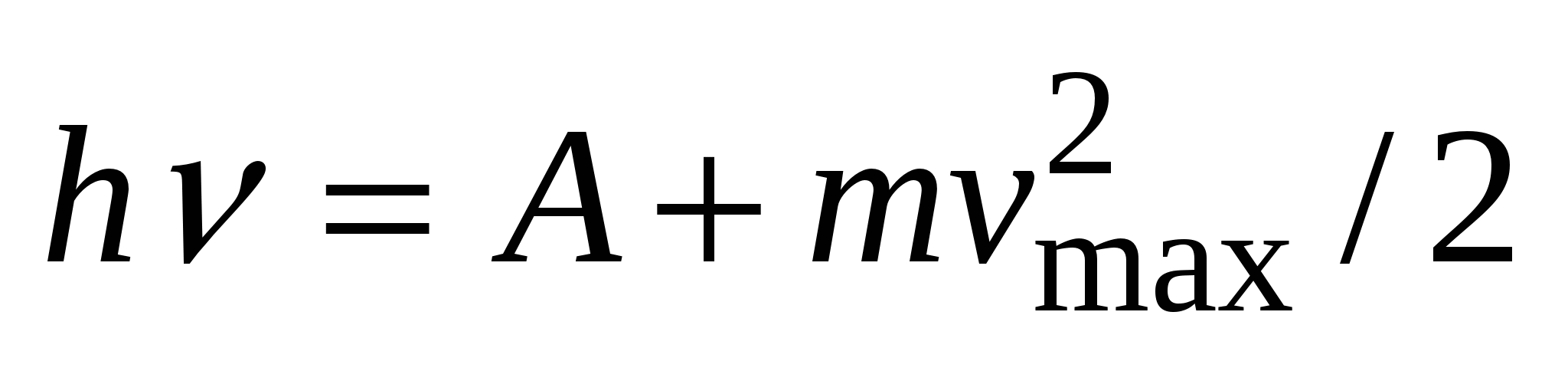 .
.
А.Эйнштейн в 1905 г. пришел к выводу, что излучение не только испускается, но и распространяется и поглощается в виде квантов. Этот вывод позволил объяснить все экспериментальные факты (фотоэффект, эффект Комптона, и др.), которые не могла объяснить классическая электродинамика, исходившая из волновых представлений о свойствах излучения.
Таким образом, распространение света следует рассматривать не как непрерывный волновой процесс, а как поток локализованных в пространстве дискретных частиц, движущихся со скоростью сраспространения света в вакууме. Впоследствии (в 1926 г.) эти частицы получили название фотонов. Фотоны обладают всеми свойствами частицы (корпускулы).
Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света получили название фотонов. Согласно закону пропорциональности массы и энергии и гипотезе Планка, энергия фотона определяется по формулам
 . .
|
Приравнивая правые части этих уравнений, получим выражение для массы фотона
 , ,
|
или с учетом, что  ,
,
 . .
|
Импульс фотона определяется по формулам:

|
Масса покоя фотона равна нулю. Квант электромагнитного излучения существует только распространяясь со скоростью света, обладая при этом конечными значениями энергии и импульса. В монохроматическом свете с частотой ν все фотоны имеют одинаковую энергию, импульс и массу.
^№ 34 Масса и импульс фотона. Давление света.
Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощается и распространяется дискретными порциями (квантами), названнымифотонами.Энергия фотона e0=hn. Его масса находится из закона взаимосвязи массы и энергии (см. (40.8)):

Фотон — элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.
Импульс фотона рg получим, если в общей формуле (40.7) теории относительности
положим массу покоя фотона  = 0:
= 0:

Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения (205.1), (205.2) и (200.2) связывают корпускулярные характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой n.
Если фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.
Рассчитаем с точки зрения квантовой теории световое давление, оказываемое на поверхность тела потоком монохроматического излучения (частота n), падающего перпендикулярно поверхности. Если в единицу времени на единицу площади поверхности тела падает N фотонов, то при коэффициенте отражения rсвета от поверхности тела rN фотонов отразится, а (1–r)N — поглотится. Каждый поглощенный фотон передаст поверхности импульс pg=hn/c, а каждый отраженный — 2pg=2hn/c (при отражении импульс фотона изменяется на –pg). Давление света на поверхность равно импульсу, который передают поверхности в 1 с N фотонов:

Nhn=Ee есть энергия всех фотонов, падающих на единицу поверхности в единицу времени, т. е. энергетическая освещенность поверхности, a Ee/c=w — объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность,

Формула (205.3), выведенная на основе квантовых представлений, совпадает с выражением, получаемым из электромагнитной (волновой) теории Максвелла. Таким образом, давление света одинаково успешно объясняется и волновой, и квантовой теорией. Как уже говорилось, экспериментальное доказательство существования светового давления на твердые тела и газы дано в опытах П. И. Лебедева, сыгравших в свое время большую роль в утверждении теории Максвелла. Лебедев использовал легкий подвес на тонкой нити, по краям которого прикреплены легкие крылышки, одни из которых зачернены, а поверхности других зеркальные. Для исключения конвекции и радиометрического эффекта использовалась подвижная система зеркал, позволяющая направлять свет на обе поверхности крылышек, подвес помещался в откачанный баллон, крылышки подбиралась очень тонкими (чтобы температура обеих поверхностей была одинакова). Световое давление на крылышки определялось по углу закручивания нити подвеса и совпадало с теоретически рассчитанным. В частности оказалось, что давление света на зеркальную поверхность вдвое больше, чем на зачерненную
№35 Эффект Комптона. Законы сохранения энергии и импульса при комптоновском рассеивании.
Квантовое (корпускулярное) свойство света проявляется в таких явлениях, как внешний и внутренний фотоэффект, тепловое излучение, эффект Комптона.
Эффект Комптона состоит в увеличении длины волны света, рассеянного свободным или слабосвязанным электронами вещества, причём излучение ? зависит от угла рассеивания.
Этот эффект для коротких ?. По классическим представлениям, электрон в поле падающей волны должен колебаться с частотой этой волны и испускать во все стороны световые волны той же частоты. Это наблюдается только для длинных ?.
Эффект Комптона объясняется только с использованием взаимодействия фотона и электронов. Пусть рассеивание происходит так: падающий фотон мгновенно поглощается электроном, затем электрон излучает рассеивание фотонов.

ЗСЭ для такого процесса рассеивания имеет вид 
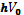 - энергетическая концентрация фотона,
- энергетическая концентрация фотона,  - энергия покоя фотона,
- энергия покоя фотона,  - энергетическая рассеивание фотона,
- энергетическая рассеивание фотона,  - энергия электрона после рассеивания. При рассеивании электрон получит большую скорость. Воспользуемся теорией относительности:
- энергия электрона после рассеивания. При рассеивании электрон получит большую скорость. Воспользуемся теорией относительности:
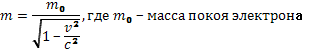 .
.
По PCB при рассеивании для системы электрон – фотон.
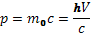 – импульс фотона.
– импульс фотона.



Отсюда - формула Комптона. Т.к.  , то
, то  , где
, где  - Комптонская длина волны. => для нерассеиванного фотона
- Комптонская длина волны. => для нерассеиванного фотона  , для рассеиванного -
, для рассеиванного -
Явление Комптона состоит в изменении длины волны рентгеновских лучей при их рассеянии на электронах, входящих в состав легких атомов. Это явление было открыто в 1923 г. Комптоновское рассеяние объясняется на основе представления о фотонах, имеющих энергию hν и импульс 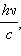 где h = 6,63·10–34 Дж·с – постоянная Планка, ν – частота фотона. Процесс рассеяния сводится к столкновению фотонов с электронами, которые можно приближенно считать свободными.
где h = 6,63·10–34 Дж·с – постоянная Планка, ν – частота фотона. Процесс рассеяния сводится к столкновению фотонов с электронами, которые можно приближенно считать свободными.
Расчет, выполненный на основе законов сохранения энергии и импульса, приводит к следующему соотношению:

|
где λ0 – длина волны падающего излучения, λ – длина волны рассеянного излучения, m – масса электрона, c – скорость света,θ – угол рассеяния.
Величина

|
называется постоянной Комптона.
В спектре рассеянного излучения наряду со смещенной спектральной линией с длиной волны λ наблюдается и несмещенная спектральная линия с длиной волны λ0. Наличие несмещенной линии объясняется тем, что часть фотонов рассеивается на электронах, сильно связанных с атомами. Соотношение интенсивностей смещенной и несмещенной линий зависит от рода материала.
Явление Комптона является ярким подтверждением квантовой теории.
При выполнении компьютерного эксперимента можно изменять длину волны λ0 падающего излучения и угол θ рассеяния фотона. На экран дисплея выводится график зависимости интенсивности I рассеянного излучения от длины волны при заданном угле рассеяния. На дисплее высвечиваются также значения длины волны λ центра смещенной линии и импульс отдачи электрона pe. В правом верхнем окне строится диаграмма импульсов.
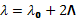 .
.
№36 Опыт Резерфорда. Планетарная модель атома. Экспериментальные закономерности линейчатого спектра водорода.
В своих опытах Резерфорд пропускал пучок альфа-частиц сквозь тонкую золотую фольгу. Золото было выбрано за пластичность, которая позволила создать очень тонкую фольгу, толщиной едва ли не в один слой молекул. За фольгой располагался специальный экран, подсвечивавшийся при бомбардировке попадающими на него альфа частицами. По теории Томсона альфа-частицы должны были беспрепятственно проходить сквозь фольгу, совсем немного отклоняясь в стороны. Однако, оказалось, что часть частиц так и вела себя, а совсем небольшая часть отскакивала назад,как будто ударившись во что-то.
То есть было установлено, что внутри атома существует нечто твердое и небольшое, от чего и отскакивали альфа-частицы. Тогда-то Резерфорд и предложил планетарную модель строения атома. Планетарная модель атома по Резерфорду объясняла результаты проведения как его экспериментов, так и опытов его коллег. До сего дня не предложено лучшей модели, хотя некоторые аспекты этой теории все равно не согласуются с практикой в некоторых очень узких областях науки. Но в основном, планетарная модель атома самая пригодная из всех. В чем же состоит эта модель?
Планетарная модель строения атома
Как следует из названия, атом сравнивается с планетой. В данном случае планету представляет из себя ядро атома. А вокруг ядра на довольно большом расстоянии вращаются электроны, как и вокруг планеты вращаются спутники. Только скорость вращения электронов в сотни тысяч раз превосходит скорость вращения самого быстрого спутника. Поэтому при своем вращении электрон создает как бы облако над поверхностью ядра. И существующие заряды электронов отталкивают такие же заряды, образованные другими электронами вокруг других ядер. Поэтому атомы не «слипаются», а располагаются на некотором расстоянии друг от друга.
И когда мы говорим о столкновении частиц, имеется в виду, что они подходят друг к другу на достаточно большое расстояние и отталкиваются полями своих зарядов. Непосредственного контакта не происходит. Частицы в веществе вообще расположены очень далеко друг от друга. Если бы каким-либо способом удалось схлопнуть вместе частицы какого-либо тела, оно бы уменьшилось в миллиарды раз. Земля стала бы меньше яблока размером. Так что основной объем любого вещества, как ни странно это звучит, занимает пустота, в которой расположены заряженные частицы, удерживающиеся на расстоянии электронными силами взаимодействия.
Исследования спектров излучения разреженных газов (т. е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода.
Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
 (209.1)
(209.1)
где R' = 1,10×107 м-1—постоянная Ридберга*. Так как v=c/A, то формула (209.1) может быть переписана для частот:
 (209.2)
(209.2)
где R = R'с = 3,29×1015 с-1 — также постоянная Ридбeрга.
Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями л, образуют группу или серию линий, называемую серией Бальмера. С увеличением л линии серии сближаются; значение n = ¥ определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.
В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. Вультрафиолетовой области спектра находится серия Лаймана:

В инфракрасной области спектра были также обнаружены:

серия Пашена
серия Брэкета
серия Пфунда
серия Хэмфри
Все приведенные выше серив в спектре атома водорода могут быть описаны одной формулой, называемойобобщенной формулой Бальмера:

где т имеет в каждой данной серии постоянное значение, т= 1, 2, 3, 4, 5, 6 (определяет серию), ппринимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии).
Исследование более сложных спектров — спектров паров щелочных металлов (на пример, Li, Na, К) — показало, что они представляются набором незакономерно расположенных линий. Ридбергу удалось разделить их на три серии, каждая из которых располагается подобно линиям бальмеровской серии.
Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Приведенный выше вид сериальных формул, удивительная повторяемость в них целых чисел, универсальность постоянной Ридберга свидетельствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физики оказалось невозможным.
№37 Теория Бора для атомов водорода и водородоподобных атомов. Ограниченность теории Бора.
Датский физик Нильс Бор (1885–1962) в 1913 г. создал первую квантовую теорию атома, связав в единое целое эмпирические закономерности линейчатых спектров водорода, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света.
В основу своей теории Бор положил три постулата, по поводу которых американский физик Л. Купер заметил: «Конечно, было несколько самонадеянно выдвигать предложения, противоречащие электродинамике Максвелла и механике Ньютона, но Бор был молод».
Первый постулат (постулат стационарных состояний): в атоме электроны могут двигаться только по определенным, так называемым разрешенным, или стационарным, круговым орбитам, на которых они, несмотря на наличие у них ускорения, не излучают электромагнитных волн (поэтому эти орбиты названы стационарными). Электрон на каждой стационарной орбите обладает определенной энергией En.
Второй постулат (правило частот): атом излучает или поглощает квант электромагнитной энергии при переходе электрона с одной стационарной орбиты на другую:
hv = E1 – E2,
где E1 и E2 – энергия электрона соответственно до и после перехода.
При E1 > E2 происходит излучение кванта (переход атома из одного состояния с большей энергией в состояние с меньшей энергией, то есть переход электрона с любой дальней на любую ближнюю от ядра орбиту); при E1 < E2 – поглощение кванта (переход атома в состояние с большей энергией, то есть переход электрона на более удаленную от ядра орбиту).
Будучи уверенным, что постоянная Планка должна играть основную роль в теории атома, Бор ввел третий постулат (правило квантования): на стационарных орбитах момент импульса электрона Ln= menrn
menrn = nh, n = 1, 2, 3, …,
где = 1,05 · 10-34 е = 9,1 · 10-31 кг – масса электрона; rп n – скорость электрона на этой орбите.
движение электрона в атоме мало похоже на движение планет по орбитам.
Точнее, электрон на орбите можно назвать электронным облаком, имеющим разную плотность.
Орбитой электрона в атоме называется геометрическое место точек, в которых с наибольшей вероятностью можно обнаружить электрон.
Энергия в атомной физике измеряется в электронвольтах.
1эВ – это энергия электрона, проходящего разность потенциалов в 1В.
1эВ = 1,6 х 10 -19 Дж
№38 Квантовая теория атома. Квантование энергии и момента импульса электронов в атоие. Главное. Орбитальное и магнитное квантовые числа. Спин. Распределение электронной плотности в атоме.
Некоторые физические величины, относящиеся к микрообъектам, изменяются не непрерывно, а скачкообразно. О величинах, которые могут принимать только вполне определенные, то есть дискретные значения (латинское "дискретус" означает разделенный, прерывистый), говорят, что они квантуются.
В 1900 г. немецкий физик М. Планк, изучавший тепловое излучение твердых тел, пришел к выводу, что электромагнитное излучение испускается в виде отдельных порций - квантов - энергии. Значение одного кванта энергии равно
ΔE = hν,
где ΔE - энергия кванта, Дж; ν - частота, с-1; h - постоянная Планка (одна из фундаментальных постоянных природы), равная 6,626·10−34 Дж·с.
Кванты энергии впоследствии назвали фотонами.
Идея о квантовании энергии позволила объяснить происхождение линейчатых атомных спектров, состоящих из набора линий, объединенных в серии.
Еще в 1885 г. швейцарский физик и математик И.Я. Бальмер установил, что длины волн, соответствующие определенным линиям в спектре атомов водорода, можно выразить как ряд целых чисел. Предложенное им уравнение, позднее модифицированное шведским физиком Ю.Р. Ридбергом, имеет вид:
1 / λ = R(1 / n12 − 1 / n22),
где λ - длина волны, см; R - постоянная Ридберга для атома водорода, равная 1,097373·105 см−1, n1 и n2 - целые числа, причем n1 < n2.
Первая квантовая теория строения атома была предложена Н. Бором. Он считал, что в изолированном атоме электроны двигаются по круговым стационарным орбитам, находясь на которых, они не излучают и не поглощают энергию. Каждой такой орбите отвечает дискретное значение энергии.
Переход электрона из одного стационарного состояния в другое сопровождается излучением кванта электромагнитного излучения, частота которого равна
ν = ΔE / h,
где ΔE - разность энергий начального и конечного состояний электрона, h - постоянная Планка. Дискретность энергии электрона является важнейшим принципом квантовой механики. Электроны в атоме могут иметь лишь строго определенные значения энергии. Им разрешен переход с одного уровня энергии на другой, а промежуточные состояния запрещены.
Зонная теория твердого тела - приближенная теория движения электронов в периодическом поле кристаллической решетки, согласно которой:
Все физические свойства твердых тел определяются внешними (валентными) электронами, которые перемещаются по всему объему кристалла от одного атома к другому и возможные уровни энергии которых образуют энергетические зоны.
1. Металлы, хорошо проводят электрический ток.
Диэлектрики (изоляторы) плохо проводят ток.
Электропроводность металлов 106 – 104 (Ом×см)-1
Электропроводность диэлектриков менее 10-10 (Ом×см)-1
Твердые тела с промежуточной электропроводностью называются полупроводниками.
Квантовое число n – главное. Оно определяет энергию электрона в атоме водорода и одноэлектронных системах (He+, Li2+ и т. д.). В этом случае энергия электрона

|
где n принимает значения от 1 до ∞. Чем меньше n, тем больше энергия взаимодействия электрона с ядром. При n = 1 атом водорода находится в основном состоянии, при n > 1 – в возбужденном.
В многоэлектронных атомах электроны с одинаковыми значениями n образуют слой или уровень, обозначаемый буквами K, L, M, N, O, P и Q. Буква K соответствует первому уровню, L – второму и т. д.
Орбитальное квантовое числоl характеризует форму орбиталей и принимает значения от 0 до n – 1. Кроме числовых lимеет буквенные обозначения
| l | = | … | |||||
| l | = | s | p | d | f | g | … |
Электроны с одинаковым значением l образуют подуровень.
Квантовое число l определяет квантование орбитального момента количества движения электрона  в сферически симметричном кулоновском поле ядра.
в сферически симметричном кулоновском поле ядра.
Квантовое число ml называют магнитным. Оно определяет пространственное расположение атомной орбитали и принимает целые значения от –l до +l через нуль, то есть 2l + 1 значений. Расположение орбитали характеризуется значением проекции вектора орбитального момента количества движения Mz на какую-либо ось координат (обычно ось z):

|
Все вышесказанное можно представить таблицей:
| ||||||||||||||||||
| Таблица 2.1 Число орбиталей на энергетических подуровнях |
Орбитали одного подуровня (l = const) имеют одинаковую энергию. Такое состояние называют вырожденным по энергии. Так p-орбиталь – трехкратно, d – пятикратно, а f – семикратно вырождены.
Граничные поверхности s-, p-, d-, f- орбиталей показаны на рис. 2.1.
s-Орбитали сферически симметричны для любого n и отличаются друг от друга только размером сферы. Их максимально симметричная форма обусловлена тем, что при l = 0 и μl = 0.
p-Орбитали существуют при n ≥ 2 и l = 1, поэтому возможны три варианта ориентации в пространстве: ml = –1, 0, +1. Все p-орбитали обладают узловой плоскостью, делящей орбиталь на две области, поэтому граничные поверхности имеют форму гантелей, ориентированных в пространстве под углом 90° друг относительно друга. Осями симметрии для них являются координатные оси, которые обозначаются px, py, pz.
d-Орбитали определяются квантовым числом l = 2 (n ≥ 3), при котором ml = –2, –1, 0, +1, +2, то есть характеризуются пятью вариантами ориентации в пространстве. d-Орбитали, ориентированные лопастями по осям координат, обозначаются dz² иdx²–y², а ориентированные лопастями по биссектрисам координатных углов – dxy, dyz, dxz.
Семь f-орбиталей, соответствующих l = 3 (n ≥ 4), изображаются в виде граничных поверхностей, приведенных на рис. 2.1. Квантовые числа n, l и ml не полностью характеризуют состояние электрона в атоме. Экспериментально установленно, что электрон имеет еще одно свойство – спин. Упрощенно спин можно представить как вращение электрона вокруг собственной оси. Спиновое квантовое числоms имеет только два значения ms = ±1/2, представляющие собой две проекции углового момента электрона на выделенную ось. Электроны с разными ms обозначаются стрелками, направленными вверх  и вниз
и вниз  .
.
В многоэлектронных атомах, как и в атоме водорода, состояние электрона определяется значениями тех же четырех квантовых чисел, однако в этом случае электрон находится не только в поле ядра, но и в поле других электронов. Поэтому энергия в многоэлектронных атомах определяется не только главным, но и орбитальным квантовым числом, а вернее их суммой: энергия атомных орбиталей возрастает по мере увеличения суммы n + l; при одинаковой сумме сначала заполняется уровень с меньшим n и большим l. Энергия атомных орбиталей возрастает согласно ряду
| 1s < 2s < 2p < 3s < 3p < 4s ≈ 3d < 4p < 5s ≈ 4d < 5p < 6s ≈ 4f ≈ 5d < 6p < 7s ≈ 5f ≈ 6d < 7p. |
Итак, четыре квантовых числа описывают состояние электрона в атоме и характеризуют энергию электрона, его спин, форму электронного облака и его ориентацию в пространстве. При переходе атома из одного состояния в другое происходит перестройка электронного облака, то есть изменяются значения квантовых чисел, что сопровождается поглощением или испусканием атомом квантов энергии.
Спин (от англ. spin — вертеть[-ся], вращение) — собственный момент импульса элементарных частиц, имеющий квантовуюприроду и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.
Спин измеряется в единицах ħ (приведённой постоянной Планка, или постоянной Дирака) и равен 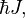 где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).
где J — характерное для каждого сорта частиц целое (в том числе нулевое) или полуцелое положительное число — так называемое спиновое квантовое число, которое обычно называют просто спином (одно из квантовых чисел).
В связи с этим говорят о целом или полуцелом спине частицы.
Существование спина в системе тождественных взаимодействующих частиц является причиной нового квантовомеханического явления, не имеющего аналогии в классической механике: обменного взаимодействия.
Электро́нная пло́тность — плотность вероятности обнаружения электрона в данной точке конфигурационного пространства.
Рассмотрим водородоподобный атом — систему из двух зарядов: положительно заряженного тяжёлого ядра, и электрона, вероятность обнаружения которого распределена сферически симметрично вокруг ядра. Таким образом, у атома водорода (и ему подобных) в основном состоянии электронная плотность зависит только от расстояния до ядра и одинакова в любой точке сферы. Это состояние электрона характеризуется нулевым орбитальным моментом импульса (так называемое s-состояние). В возбуждённых состояниях с отличным от нуля орбитальным моментом электрона (p-, d-, f-… состояния) сферическая симметрия электронной плотности отсутствует. В достаточно сложных молекулах электронная плотность, как правило, несимметрична, а форма электронного облака может меняться. Например, при замещении трёх атомов водорода метильной группы уксусной кислоты на чрезвычайно электроотрицательные атомы хлора её константа диссоциации (pK) снижается с 4,76 до почти 1 в результате индуктивно вызванного снижения силы притяжения H+ к карбоксильной группе; сила кислоты возрастает. Существуют две простые, но логичные точки зрения на это явление. По одной из них, увеличение силы кислоты отражает смещение плотности распределения единственного избыточного электрона карбоксильного кислорода в сторону от H+, и сила притяжения протона ослабевает. Согласно другой точке зрения, причиной этого явления служит не смещение, а «разжижение» «облака отрицательного электричества», то есть снижение электронной плотности вокруг однозарядного атома кислорода.
В качестве модели состояния электрона в атоме, в квантовой механике принято представление об электронном облаке, плотность соответствующих участков которого пропорциональна вероятности нахождения там электрона.
Электронное облако часто изображают в виде граничной поверхности. При этом обозначение электронной области при помощи точек опускают . Пространство вокруг ядра, в котором наиболее вероятно пребывание электрона, называют атомной орбиталью (смысл которого вытекает из волнового уравнения Шрёдингера).
Применяются графические изображения распределения электронной плотности относительно ядра.
Кривая радиального распределения вероятности показывает, что электрон находится в тонком концентрическом шаровом слое радиуса r толщины dr вокруг ядра атома водорода[1].
Проекция максимума кривой соответствует боровскому радиусу α0=0,53 Å.
№39 Последовательность заполнения электронных уровней атомов. Периодическая система элементов.
Атом – наименьшая частица химического элемента, носитель его свойств. Является самой простой электро енйтральной химической микросистемой, подчиняющейся законам квантовой механики.
Для электрона в атоме справедлив принцип двойственности: электрон является одновременно и материальной частицей малой массы и электромагнитной волной.
Принцип неопределнности Гейзенберга: В каждый конкретный момент времени нельзя с одинаковой точностью определить место нахождения электронов (координаты x,y,z) и его скорость (или импульс).
Движение электорона в атоме может быть представлено в виде электронного облака.
Область электронного облака, в которой электрон проводит более 95% времени нывается электронной орбиталью (Э.О.). Больший размер орбитали характеризует большую энергию электрона. Орбитали близкого размера образуют энергетические уровни, которые состоят из подуровней.
Для описания состояния электрона в атоме используются 4 квантовых числа (n,l,m,s). Первые три соответствуют трем степеням свободы электрона в трехмерном пространстве, а четвертое соответсвует вероятности вращения электрона вокруг воображаемой собственной оси. Квантовые числа:
1. “n” – главное квантовое число. Характеризует уровень энергии электрона в поле атома (удаленность от ядра). Математическая зависимость энергии связи с ядром: Ea=-13,6/n2 Эв, n=1,2,… Для реальных элементов n=1,…,7. n=номеру периода.
2. “l” – орбитальное квантовое число. Характризует тип подуровня (форма электронного облака). l=0,1,2,…,(n-1). Обозначается буквами. При этом l=0 соответствует s, 1-p, 2-d, 3-f, 4-q, 5-h.
3. “m” – магнитное квантовое число. Характеризует пространственное расположение орбитали. m=± 0, ± 1, ± 2,…, ± l. Cумма орбиталей на подуровне: å =2l+1.
4. “s” – спиновое квантовое число. Характеризует вероятность вращения электрона вокруг своей оси в двух противоположенных направлениях. s=± 1/2. “+” – по часовой стрелке, “-“ – против часовой стрелке. Вращение сообщает электрону собственный магнитный момент, который называется спином электрона.
Принцип Паули (запрет): у атомов, имеющих больше одного электрна не может быть двух электронов с одинаковыми значениями всех четырех квантовых чисел. Или так: на одной орбитали могут находится только два электрона, причем с противоположенными спинами.
Принцип минимума энергии: последовательное заполенние электронов в атоме должно отвечать как минимому энергии самого электрона, так и минимому энерги атома в целом. Или так: минимум энергии соответствует максимому устойчивости. Заполение идет в соответсвии с уравнением энергии орбитали: ns<(n-1)d» (n-2)f<np. На внешнем уровне не может быть более 8 электронов.
Правило Клечковского: сначала заполняются те подуровни, сумма n+l которых наименьшая. Если для двух подуровней сумма n+l равна, то сначала заполняется подуровень с меньшим n.
Правило Хунда: в основном (невозбужденном) состоянии атома на подуровнях np, nd и nf всегда имеется максимальное количество неспаренных электронов (максимальный неспаренный спин).
Подуровни p, d и f состоят из нескольких орбиталей, энергия которых одинакова, поэтому эти подуровни называются “вырожденными”: p подуровень вырожден трехкратно, d пятикратно и f семикратно. Для электронов этих подуровней соблюдается правило Хунда.
Валентность – способность образовывать химические связи.
Основное состояние – состояние с минимальной энергией, т.е электроны находятся ближе к ядру.
Возбужденное состояние – состояние, при котором все или часть электронов в атоме распарены и находятся на подуровне с большей энергией, т.е дальше от ядра.
Максимальная валентность наблюдается в возбужденном состоянии и как правило совпадает с номером группы, в которой находится элемент.
ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВпредставляет собой классификацию химических элементов в соответствии с периодическим законом, устанавливающим периодическое изменение свойств химических элементов по мере увеличения их атомной массы, связанного с увеличением заряда ядра их атомов; поэтому заряд ядра атома совпадает с порядковым номером элемента в периодической системе и называется атомным номером элемента. Периодическая система элементов оформляется в виде таблицы (периодическая таблица элементов), в горизонтальных рядах которой
периодах – происходит постепенное изменение свойств элементов, а при переходе от одного периода к другому – периодическое повторение общих свойств; вертикальные столбцы – группы – объединяют элементы со сходными свойствами. Периодическая система позволяет без специальных исследований узнать о свойствах элемента только на основании известных свойств соседних по группе или периоду элементов. Физические и химические свойства (агрегатное состояние, твердость, цвет, валентность, ионизация, стабильность, металличность или неметалличность и т.д.) можно предсказывать для элемента на основании периодической таблицы.
В конце 18 и начале 19 вв. химики пытались создавать классификации химических элементов в соответствии с их физическими и химическими свойствами, в частности на основе агрегатного состояния элемента, удельного веса (плотности), электропроводности, металличности – неметалличности, основности – кислотности и т.д.
№40 Получение рентгеновского излучения. Сплошной и характеристический рентгеновский спектр. Формула Мозли. Применение рентгеновского излучения.
Рентгеновские лучи возникают при сильном ускорении заряженных частиц (в основном электронов) либо же при высокоэнергетичных переходах вэлектронных оболочках атомов или молекул. Оба эффекта используются в рентгеновских трубках, в которых электроны, испущенные раскалённым катодом, ускоряются (при этом рентгеновские лучи не испускаются, т. к. ускорение слишком мало) и ударяются об анод, где они резко тормозятся (при этом испускаются рентгеновские лучи: т. н. тормозное излучение) и в то же время выбивают электроны из внутренних электронных оболочек атомов металла, из которого сделан анод. Пустые места в оболочках занимаются другимиэлектронами атома. При этом испускается рентгеновское излучение с определённой, характерной для материала анода, энергией (характеристическое излучение, частоты определяются законом Мозли: ν−√=A(Z−B), где Z —атомный номер элемента анода, A и B — константы для определённого значения главного квантового числа n электронной оболочки). В настоящее время анодыизготовляются главным образом из керамики, причём та их часть, куда ударяют электроны, — из молибдена. В процессе ускорения-торможения лишь 1%кинетической энергии электрона идёт на рентгеновское излучение, 99% энергии превращается в тепло.
Рентгеновское излучение можно получать также и на ускорителях заряженных частиц. Т. н. синхротронное излучение возникает при отклонении пучка частиц в магнитном поле, в результате чего они испытывают ускорение в направлении, перпендикулярном их движению. Синхротронное излучение имеет сплошной спектр с верхней границей. При соответствующим образом выбранных параметрах (величина магнитного поля и энергия частиц) в спектре синхротронного излучения можно получить и рентгеновские лучи.
При помощи рентгеновских лучей можно просветить человеческое тело, в результате чего можно получить изображение костей, а в современных приборах и внутренних органов (см. также рентген). При этом используется тот факт, что у содержащегося преимущественно в костях элемента кальция (Z=20) атомный номер гораздо больше, чем атомные номера элементов, из которых состоят мягкие ткани, а именно водорода (Z=1), углерода (Z=6), азота (Z=7), кислорода (Z=8). Кроме обычных приборов, которые дают двумерную проекцию исследуемого объекта, существуют компьютерные томографы, которые позволяют получать объёмное изображение внутренних органов.
Выявление дефектов в изделиях (рельсах, сварочных швах и т. д.)) с помощью рентгеновского излучения называется рентгеновской дефектоскопией.
В материаловедении, кристаллографии, химии и биохимии рентгеновские лучи используются для выяснения структуры веществ на атомном уровне при помощи дифракционного рассеяния рентгеновского излучения (рентгеноструктурный анализ). Известным примером является определение структуры ДНК.
Кроме того, при помощи рентгеновских лучей может быть определён химический состав вещества. В электронно-лучевом микрозонде(либо же в электронном микроскопе) анализируемое вещество облучается электронами, при этом атомы ионизируются и излучаютхарактеристическое рентгеновское излучение. Вместо электронов может использоваться рентгеновское излучение. Этот аналитический метод называется рентгено-флюоресцентным анализом.
характеристический спектр — линейчатый рентгеновский спектр, возникающий при переходах электронов верхних оболочек атома на более близко расположенные к его ядру K=, L=, М=, N оболочки. Частоты линий характеристического спектра химических элементов подчиняются Мозли закону
Сплошной рентгеновский спектр возникает вследствие торможения электронов, разогнанных в трубке электрическим полем, при их ударе об антикатод. Из квантовой природы излучения вытекает и существование коротковолновой границы сплошного рентгеновского спектра. [1]
Сплошной рентгеновский спектр поэтому называют тормозным спектром. Этот вывод находится в согласии с классической теорией излучения, так как при торможении движущихся зарядов должно действительно возникать излучение со сплошным спектром. [2]
Почему сплошной рентгеновский спектр, испускаемый трубкой, имеет резкую границу со стороны коротких волн. Чем определяется ее положение. [3]
№ 41 основные характеристики и свойства атомных ядер. Размеры, масса и энергия связи ядер. Дефект массы. Взаимодействие нуклонов. Модели атомного ядра.
Ядром называется центральная часть атома, в которой сосредоточена практически вся масса атома и его положительный заряд. Атомное ядро любого химического элемента состоит из протонов и нейтронов, которые считаются двумя зарядовыми состояниями одной частицы – нуклона.
Протон (  или
или  ) - атомное ядро самого легкого изотопа водорода, его масса
) - атомное ядро самого легкого изотопа водорода, его масса  , заряд равен элементарному заряду
, заряд равен элементарному заряду  . Протон обладает полуцелым спином
. Протон обладает полуцелым спином 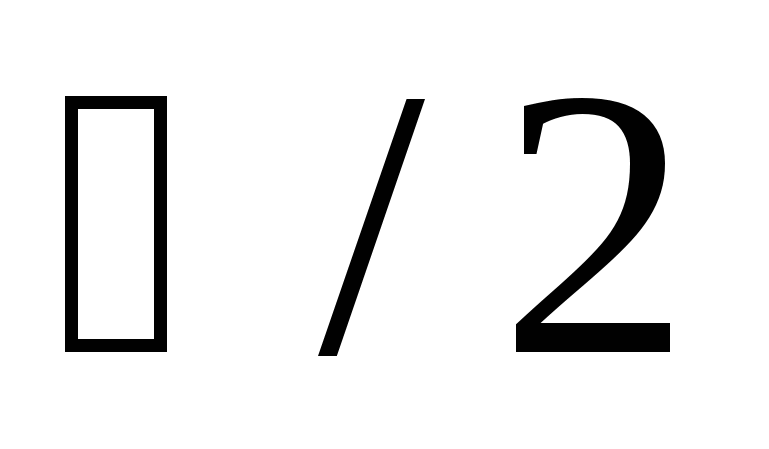 и магнитным моментом
и магнитным моментом 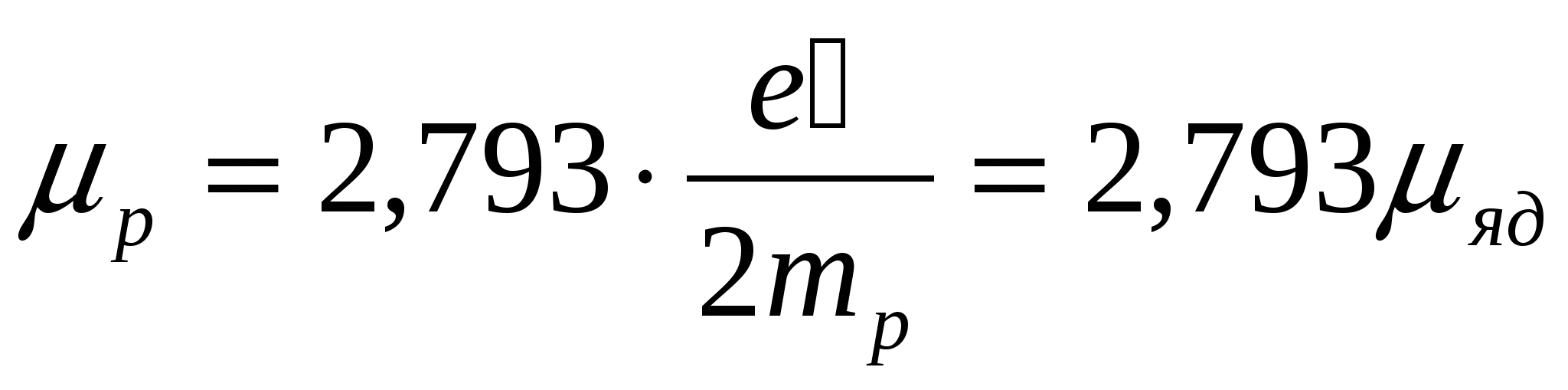 .
.
Нейтрон (  ) – частица, встречающаяся в природе только в составе атомных ядер и в небольшом количестве в составе космического излучения. Его электрический заряд равен нулю, масса
) – частица, встречающаяся в природе только в составе атомных ядер и в небольшом количестве в составе космического излучения. Его электрический заряд равен нулю, масса  , спин
, спин 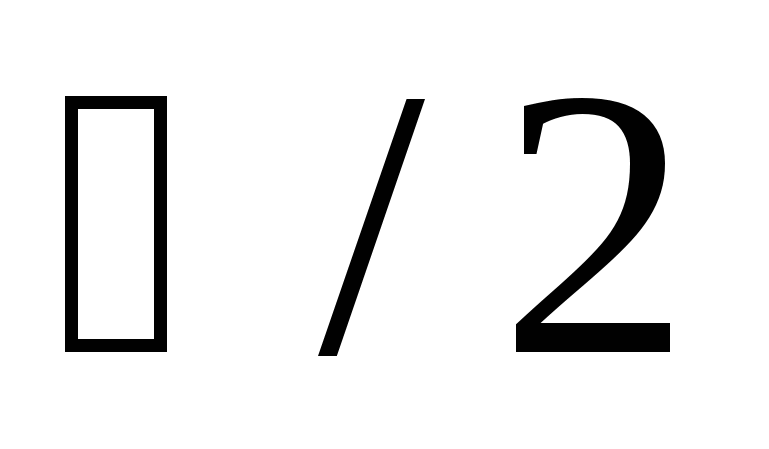 , магнитным моментом
, магнитным моментом  . Магнитный момент и спин нейтрона направлены в противоположные стороны.
. Магнитный момент и спин нейтрона направлены в противоположные стороны.
«Свободный», т.е. не входящий в состав атомного ядра, нейтрон самопроизвольно превращается в протон
 .
.
Период его полураспада равен 12 минутам. Нейтроны и протоны, таким образом, способны к взаимным превращениям.
Заряд ядра +Zе определяется порядковым номером химического элемента Z в периодической таблице Менделеева, и равен числу протонов в ядре. Массовое число равно суммарному числу нуклонов в ядре А = Z + N, где N – число нейтронов.
Ядра одного и того же элемента с различным числом нейтронов называются изотопами, ядра различных элементов с одинаковым массовым числом называются изобарами.
Радиус ядра пропорционален числу нуклонов в нем 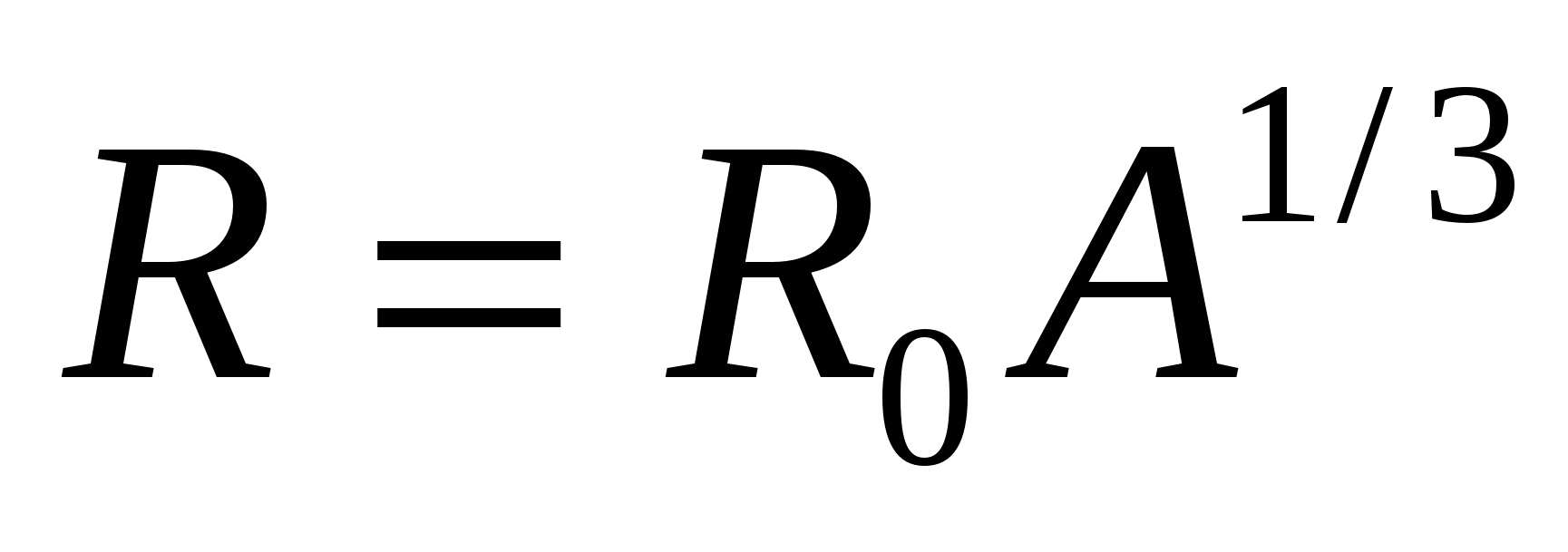 , где
, где  Плотность ядерного вещества составляет по порядку величину
Плотность ядерного вещества составляет по порядку величину  , она значительно превосходит плотности самых плотных веществ.
, она значительно превосходит плотности самых плотных веществ.
Ядро атома имеет собственный момент импульса – спин ядра
 ,
,
где I= 0, 1/2, 1, 3/2, 2 … – внутреннее квантовое число.
Магнитный момент ядра определяется магнитными моментами ядерных частиц.
Устойчивость ядер, несмотря на отталкивание одноименных заряженных протонов, обеспечивают ядерные силы, относящиеся к классу сильных взаимодействий. Ядерные силы являются короткодействующими силами притяжения, обладающими зарядовой независимостью. Они не являются центральными силами, зависят от взаимной ориентации спинов взаимодействующих нуклонов, и имеют способность к насыщению.
Для того чтобы ядро расщепить на отдельные нуклоны необходимо затратить энергию, называемую энергией связи ядра
 ,
,
где 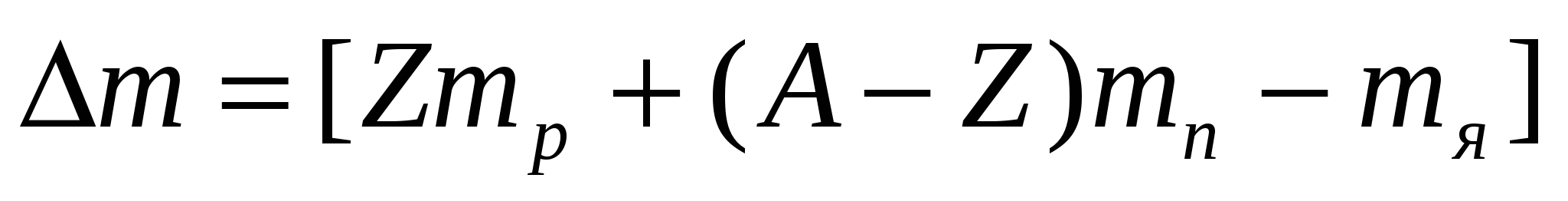 - дефект масс - величина, на которую уменьшается масса всех нуклонов при образовании из них атомного ядра. Одной атомной единице массы соответствует атомная единица энергии 1 а.е.м. = 931,5 МэВ.
- дефект масс - величина, на которую уменьшается масса всех нуклонов при образовании из них атомного ядра. Одной атомной единице массы соответствует атомная единица энергии 1 а.е.м. = 931,5 МэВ.
Энергия связи, приходящаяся на один нуклон, называется удельной энергией связи. Чем больше удельная энергия связи, тем устойчивей ядро. Наиболее стабильные ядра с атомной массой А~60. Из зависимости удельной энергии связи от атомной массы (рис.1) следует, что энергетически выгодны процессы слияния легких ядер в более тяжелые, и деление тяжелых ядер на более легкие.
Для описания свойств ядра рассматриваются капельная и оболочная модели ядра. Капельная модель трактует ядро, как каплю электрически заряженной жидкости с ядерной плотностью, подчиняющуюся законам квантовой механики. Эта модель объясняет механизмы ядерных реакций, реакции деления, энергию связи в ядре. Оболочная модель предполагает распределение нуклонов в ядре по дискретным энергетическим уровням (оболочкам), заполненными нуклонами, согласно принципу Паули, и связывает устойчивость ядер с заполнением этих уровней. Эта модель объясняет магнитные моменты атомов, спины, различную устойчивость атомных яд
Дефе́кт ма́ссы — разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, имассой покоя атомного ядра этого нуклида, выраженная в атомных единицах массы. Обозначается обычно  .
.

Согласно соотношению Эйнштейна, энергия связи пропорциональна дефекту массы:

где  — дефект массы и с — скорость света в вакууме.
— дефект массы и с — скорость света в вакууме.
Дефект массы характеризует устойчивость ядра.
Дефект массы, отнесённый к одному нуклону, называется упаковочным множителем.
ер, периодичность свойств.
№42 Радиоактивный распад и деление атомных ядер. Закон радиоактивного распада. Активность. Период полураспада. Среднее время жизни радиоактивного ядра.
К основным видам радиоактивного распада относятся a-распад, b-распад, спонтанное деление атомных ядер и протонный распад. Часто эти виды радиоактивного распада сопровождаются испусканием g-лучей, т.е. жесткого (с малой длиной волы) электромагнитного излучения.
При a-распаде ядро атома испускает два протона и два нейтрона, связанные в ядро атома гелия 42Не; это приводит к уменьшению заряда исходного радиоактивного ядра на 2, а его массового числа на 4. Таким образом, в результате a-распада образуется атом элемента, смещенного на два места от исходного радиоактивного элемента к началу периодической системы.
Возможность b-распада связана с тем, что по современным представлениям протон и нейтрон представляют собой два состояния одной и той же элементарной частицы — нуклона (от лат. nucleus — ядро). При известных условиях (например, когда избыток нейтронов в ядре приводит к его неустойчивости) нейтрон может превращаться в протон, одновременно «рождая» электрон:
нейтрон ® протон + электрон или n ®р+ е-
Таким образом, при b-распаде один из нейтронов, входящих в состав ядра, превращается в протон; возникающий при этом электрон вылетает из ядра, положительный заряд которого на единицу возрастает.
Возможно также превращение протона в нейтрон: протон ® нейтрон + позитрон или p® n + n+, где n+ — позитрон — элементарная частица с массой, равной массе электрона, но несущая положительный электрический заряд; по абсолютной величине заряды электрона и позитрона одинаковы. Процесс превращения протона в нейтрон с образованием позитрона может происходить в тех соединениях, когда неустойчивость ядра вызвана избыточным содержанием в нем протонов. При этом один из протонов, входящих в состав ядра, превращается в нейтрон, возникающий позитрон вылетает за пределы ядра, а заряд ядра на единицу уменьшается. Такой вид радиоактивного распада называется позитронным b-распадом (или b+-распадом) в отличие от ранее рассмотренного электронного b-распада (b--распада). Этот вид радиоактивного распада наблюдается у некоторых искусственно полученных радиоактивных изотопов.
Изменение заряда ядра при b-распаде приводит к тому, что в результате b-распада образуется атом элемента, смещенного на одно место от исходного радиоактивного элемента к концу периодической системы (в случае b--распада) или к ее началу (в случае b+-распада).
К уменьшению заряда ядра на единицу приводит не только b+-распад, но и электронный, захват, при котором один из электронов атомной электронной оболочки захватывается ядром; взаимодействие этого электрона с одним из содержащихся в ядре протонов приводит к образованию нейтрона:
Электрон чаще всего захватывается из ближайшего к ядру К-слоя (.К-захват), реже из L или М-слоев.
Спонтанным делением называется самопроизвольный распад ядер тяжелых элементов на два (иногда на три или четыре) ядра элементов середины периодической системы. Варианты такого деления очень разнообразны, так что общих правил смещения по периодической системе не существует; чаще всего происходит распад исходного ядра на тяжелый и легкий осколки, несущие, соответственно, ок
Дата добавления: 2015-01-29; просмотров: 644; Мы поможем в написании вашей работы!; Нарушение авторских прав |
