
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет рабочих режимов разомкнутых и простых замкнутых электрических сетей
Лекция 8
8.1 Задача расчета режима сети, основные допущения
Основную задачу расчета режима сети составляет определение параметров режима. Как уже указывалось, к таким параметрам относятся: токи на участках сети, активные и реактивные мощности, напряжение в узлах сети, частота и др.
Исходными данными для расчета служат: расчетные мощности нагрузок, заданные величины напряжения в отдельных точках, схема электрических соединений сети, характеризующая взаимную связь ее элементов и другие величины.
Основным методом для электрического расчета сети является метод последовательных приближений (итераций), который предусматривает постепенный переход от более грубых ответов на поставленную задачу к более точным решениям. Первое приближение (нулевая итерация) при этом может быть получено на основании тех или иных представлений о возможных значениях искомых величин. Применительно к электрическим сетям в качестве первого приближения принимают равенство напряжений во всех точках сети номинальному напряжению. Это позволяет определить токи нагрузок и остальные параметры режима сети, в том числе и напряжения на зажимах нагрузки. Найденные напряжения являются уже вторым приближением к истинному решению. На основании этого можно снова найти токи и продолжать выполнять расчеты до тех пор, пока результаты последующих приближений не будут с заданной точностью отличаться от результатов предыдущих.
Практически при проведении расчетов электрических сетей можно ограничится второй и первой итерациями. К числу таких расчетов относятся расчеты сетей 35 кВ и ниже, а в ряде случаев – проектные расчеты сетей напряжением 110 и 220 кВ. При анализе режимов сетей 35 кВ и ниже ограничиваются первым приближением. Связано это с тем, что требования потребителей к качеству напряжения определяет необходимость обеспечивать для всех точек таких сетей напряжения, мало отличающихся от номинальных, которые принимаются при расчетах первого приближения. Получаемая при этом ошибка лежит в пределах точности расчета. Ошибка, получаемая при ограничении расчетов сетей 110 и 220 кВ вторым приближением, также оказывается в пределах точности расчета.
8.2 Расчет линии с нагрузкой на конце по потере напряжения
Рассмотрим простейшую линию трехфазного тока с симметричной нагрузкой на конце (рисунок 8.1).

Рисунок 8.1
Нагрузка задана либо током I и cosj при фазном напряжении U 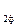 на конце линии, либо мощностью S = P + jQ.
на конце линии, либо мощностью S = P + jQ.
Расчет проводится с помощью векторной диаграммы токов и напряжений для одной фазы линии, что допускается, так как нагрузка во всех фазах симметрична.

Рисунок 8.2 - Векторная диаграмма линии с нагрузкой на конце
Известны ток нагрузки I, cosj и напряжение U 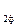 . Необходимо определить U
. Необходимо определить U  . По действительной оси откладываем вектор заданного напряжения в конце линии U
. По действительной оси откладываем вектор заданного напряжения в конце линии U 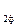 (ОА). Из начала координат откладываем вектор тока I под углом j. Его активная составляющая направлена по действительной оси I
(ОА). Из начала координат откладываем вектор тока I под углом j. Его активная составляющая направлена по действительной оси I  , а реактивная составляющая -jI
, а реактивная составляющая -jI  - по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя.
- по мнимой оси в отрицательном направлении. Таким образом, при принятом расположении вектора напряжения и тока на векторной диаграмме знак минус у мнимой части комплекса тока характеризует индуктивный (отстающий) ток нагрузки потребителя.
Далее из точки А откладываем параллельно вектору тока I вектор падения напряжения в активном сопротивлении линии IR (АВ) и под углом 90  к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного падения напряжения в рассматриваемой линии IZ (АС). Чтобы найти напряжение U
к нему в сторону опережения – вектор падения напряжения в реактивном сопротивлении IX (ВС). Соединив точку А с точкой С, получим вектор полного падения напряжения в рассматриваемой линии IZ (АС). Чтобы найти напряжение U  , соединим точку С с началом координат, получаем вектор фазного напряжения в начале линии U
, соединим точку С с началом координат, получаем вектор фазного напряжения в начале линии U  (ОС).
(ОС).
Падение напряжения в линии
IZ = 
может быть разложено на составляющие:
а) продольную DU  = АD
= АD
б) поперечную d U  = DC
= DC
т.е. IZ = DU  + jd U
+ jd U 
Определим эти составляющие. Для этого опустим перпендикуляры из точек В и С на действительную и мнимую оси. В результате получим отрезки:
АЕ = IRcosj; ED = BF = IXsinj;
CF = IXcosj; BE = DF = IRsinj.
Отсюда продольная составляющая
DU  = AD = AE + ED = IRcosj + IXsinj = I
= AD = AE + ED = IRcosj + IXsinj = I  R + I
R + I  X (8.1)
X (8.1)
d U  = DC = CF - DF = IXcosj - IRsinj = I
= DC = CF - DF = IXcosj - IRsinj = I  X + I
X + I  R (8.2)
R (8.2)
Напряжение в начале линии

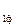 = U
= U 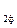 + DU
+ DU  + jdU
+ jdU  ,
,
а модуль напряжения
U 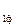 =
=  . (8.3)
. (8.3)
В результате построения диаграммы выше был получен вектор полного падения напряжения в линии. Следует отметить, что под падением напряжения понимают геометрическую разность потенциалов между началом и концом линии.
При расчете сетей 35 кВ и ниже обычно вводятся упрощения, заключающиеся в том, что напряжение в начале линии определяют не по падению напряжения, а по потере напряжения. Под потерей напряжения понимают алгебраическую разность абсолютных значений напряжений в начале и в конце линии.
Для определения потери напряжения на диаграмме совместим отрезок ОС с осью действительных величин (отрезок О  ).
).
Отрезок А  = О
= О  - ОА = U
- ОА = U 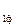 - U
- U 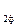
представляет собой потерю напряжения.
Так как для сетей 35 кВ и ниже углы между U 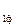 и U
и U 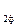 очень малы, а значит мал и отрезок D
очень малы, а значит мал и отрезок D  , то можно считать, что потеря напряжения приблизительно равна продольной составляющей падения напряжения
, то можно считать, что потеря напряжения приблизительно равна продольной составляющей падения напряжения
АD » A  » DU
» DU  » IRcosj + IXsinj (8.4)
» IRcosj + IXsinj (8.4)
Потеря линейного напряжения
DU =  DU
DU  =
=  I(Rcosj + Xsinj) . (8.5)
I(Rcosj + Xsinj) . (8.5)
Векторная диаграмма линейных напряжений будет выглядеть аналогично диаграмме фазных напряжений.
При задании нагрузки активной и реактивной мощностью Р+jQ величина потери напряжения определяется следующим образом
Так как I  = Icosj =
= Icosj =  и I
и I  = Isinj =
= Isinj =  , то, подставив эти значения в (4.5), получим
, то, подставив эти значения в (4.5), получим
DU =  (IRcosj + IXsinj) =
(IRcosj + IXsinj) = 
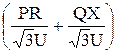 ,
,
или DU =  . (8.6)
. (8.6)
Часто при расчетах напряжение у потребителей бывает неизвестно, то вместо действительного в конце линии можно принимать номинальное напряжение
DU =  . (8.7)
. (8.7)
При расчетах сети с несколькими нагрузками величина потери напряжения определяется как сумма потерь напряжений на всех участках сети
DU =  (8.8)
(8.8)
Лекция 9
9.1 Расчеты режима разомкнутых электрических сетей.
При расчете режима сетей 110 – 220 кВ можно выделить два характерных расчетных случая: расчет сети по заданному напряжению в конце линии (или расчет по данным конца) и расчет, в котором заданным является напряжение в начале линии (расчет по данным начала).
На рисунке 9.1 представлена расчетная схема разомкнутой сети с n нагрузками (а) и ее схема замещения (б).
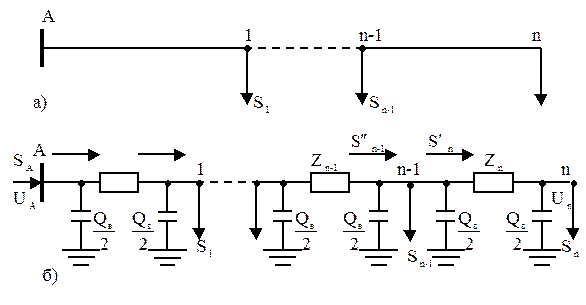
Рисунок 9.1
Рассмотрим случай расчета по данным конца. Исходными данными являются: напряжение в конце линии U  , расчетные мощности нагрузок, а также параметры сети. Расчет ведется от конца линии. По известному напряжению U
, расчетные мощности нагрузок, а также параметры сети. Расчет ведется от конца линии. По известному напряжению U  определяются потери мощности на последнем участке линии n
определяются потери мощности на последнем участке линии n
 (9.1)
(9.1)
Находим мощность в начале участка n
 , (9.2)
, (9.2)
где Q  - зарядная мощность на участке n.
- зарядная мощность на участке n.
Мощность в конце участка (n-1) по балансу мощности в узле (n-1) определяется
 . (9.3)
. (9.3)
Падение напряжения на концевом участке n определяется
D 
 = DU
= DU  + jdU
+ jdU  =
=  + j
+ j  . (9.4)
. (9.4)
По известному напряжению U  и падению напряжения на участке n определяется напряжение в узле n-1 U
и падению напряжения на участке n определяется напряжение в узле n-1 U 
 =
=  + D
+ D  = U
= U  + DU
+ DU  + jdU
+ jdU  (9.5)
(9.5)
или модуль напряжения
U  =
=  . (9.6)
. (9.6)
Определением напряжения  закачивается расчет режима концевого участка сети. При этом оказываются известными все необходимые данные для расчета следующего участка. Расчет участка n-1 выполняется по тем же формулам, что и для участка n. Аналогично ведутся расчеты для всех остальных участков. Окончанием расчета является определение мощности
закачивается расчет режима концевого участка сети. При этом оказываются известными все необходимые данные для расчета следующего участка. Расчет участка n-1 выполняется по тем же формулам, что и для участка n. Аналогично ведутся расчеты для всех остальных участков. Окончанием расчета является определение мощности  и напряжения
и напряжения 
 .
.
В расчетах сети по данным начала, в которых известной величиной является напряжение в точке питания 
 , используется метод последовательных приближений, причем расчеты выполняются в два этапа.
, используется метод последовательных приближений, причем расчеты выполняются в два этапа.
В качестве первого приближения (на первом этапе расчета) принимается, что напряжения во всех узлах равны номинальному напряжению сети. При этом условии находится распределение мощностей в сети.
В соответствии с обозначениями на рисунке 9.1 расчет ведется в следующей последовательности. Определяются потери мощности на концевом участке сети
DP  =
=  ,
,
DQ  =
=  . (9.7)
. (9.7)
Далее определяется мощность  в начале этого участка в соответствии с (9.2). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (9.3). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится
в начале этого участка в соответствии с (9.2). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (9.3). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится  .
.
На следующем этапе расчета определяются напряжения в узлах нагрузки во втором приближении. Исходными данными для расчета являются: напряжение 
 и найденные в предыдущем этапе расчета мощности в конце каждого из участков. Для головного участка сети
и найденные в предыдущем этапе расчета мощности в конце каждого из участков. Для головного участка сети

 =
= 
 - D
- D 
 , (9.8)
, (9.8)
где D 
 - падение напряжения на головном участке сети.
- падение напряжения на головном участке сети.

 =
= 
 - DU
- DU  - jdU
- jdU  (9.9)
(9.9)
или в раскрытой форме

 = U
= U  -
-  -
-  . (9.10)
. (9.10)
Модуль напряжения в точке 1
U  =
=  . (9.11)
. (9.11)
Аналогично определяются напряжения в других узловых точках сети.
Лекция 10
10.1 Расчеты режимов кольцевых сетей
Наиболее простой замкнутой сетью является кольцевая сеть. Она имеет один замкнутый контур (рисунок 10.1а). В качестве питательного пункта может быть либо электростанция, либо шины подстанции системы. Если такую сеть разрезать по источнику питания и развернуть, то она будет иметь вид как линии с двусторонним питанием, у которой напряжения по концам равны по величине и по фазе (рисунок 10.1б).

Рисунок 10.1
Для расчета сети возьмем схему, приведенную на рисунке 10.2. Здесь мощности  ,
,  ,
,  - расчетные нагрузки подстанций. Направление потоков мощности на участках сети принято условно. Действительное направление определяется в результате расчета.
- расчетные нагрузки подстанций. Направление потоков мощности на участках сети принято условно. Действительное направление определяется в результате расчета.
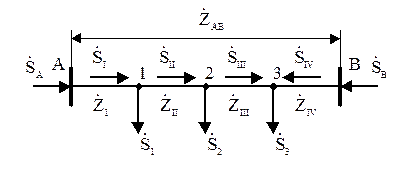
Рисунок 10.2
Исходными данными для расчета сети являются напряжение в центре питания, мощности нагрузок, параметры сети.
Так как напряжения в узлах нагрузки неизвестны, то расчет должен выполняться с помощью метода последовательных приближений.
Так же как и при расчете разомкнутых сетей принимают условие равенства напряжений вдоль линии. Это напряжение принимают равным номинальному. При этих допущениях ток на участках сети определяется
 .
.
Условие равенства напряжений по концам линии означает равенство нулю падения напряжения в схеме (рисунок 4.3).
На основании второго закона Кирхгофа запишем
 +
+  +
+  -
-  =0
=0
или
 +
+  +
+  -
-  =0 (10.1)
=0 (10.1)
Выразим входящие в это уравнение мощности 2,3 и 4 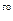 участков линии через мощность
участков линии через мощность  и известные мощности нагрузок
и известные мощности нагрузок  ,
,  ,
,  .
.
При неучете потерь мощности можно записать
 +
+  =
=  +
+  +
+  ,
,
откуда
 =
=  +
+  +
+  -
-  . (10.2)
. (10.2)
На основании первого закона Кирхгофа
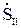 =
=  -
-  , (10.3)
, (10.3)
 =
=  -
-  -
-  . (10.4)
. (10.4)
Подставим (10.2 – 10.4) в исходное уравнение (10.1) и после преобразований получим
 (
(  +
+  +
+  +
+  )-
)-  (
(  +
+  +
+  )-
)-  (
(  +
+  )-
)- 
 =0
=0
откуда с учетом обозначений на схеме
 =
=  =
=  (10.5)
(10.5)
Аналогично можно получить
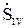 =
=  =
=  . (10.6)
. (10.6)
В общем случае при n нагрузках на кольцевой сети
 (10.7)
(10.7)
где 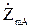 и
и  - сопротивления от точки m, в которой включена некоторая промежуточная нагрузка
- сопротивления от точки m, в которой включена некоторая промежуточная нагрузка  , до точек питания А и В соответственно.
, до точек питания А и В соответственно.
После определения мощностей, протекающих по головным участкам сети, определяются мощности на остальных участках с помощью закона Кирхгофа. На этом заканчивается первый этап расчета режима этой линии. На втором этапе определяются потери мощности и напряжения в узловых точках сети. Допустим, что в результате первого этапа расчета найдено распределение мощностей, как показано на рисунке 10.3а.

Рисунок 10.3
К точке 2 мощность поступает с двух сторон. Эта точка называется точкой потокораздела и на рисунке отличается зачерненным треугольником.
Для расчета напряжений в узловых точках условно разрежем схему (рисунок 10.3а) по точке потокораздела (рисунок 10.3б).
Получим схему, состоящую из двух независимых частей, каждая из которых характеризует разомкнутую сеть с заданными нагрузками и напряжениями U  =U
=U  на шинах общего источника питания. Следовательно, дальнейший расчет кольцевой сети должен проводиться так же, как для разомкнутых сетей по данным начала. Для сетей 110-220 кВ учитываются потери мощности и определяются напряжения в узловых точках. Для сетей 35 кВ и ниже напряжения рассчитываются без учета потерь мощности.
на шинах общего источника питания. Следовательно, дальнейший расчет кольцевой сети должен проводиться так же, как для разомкнутых сетей по данным начала. Для сетей 110-220 кВ учитываются потери мощности и определяются напряжения в узловых точках. Для сетей 35 кВ и ниже напряжения рассчитываются без учета потерь мощности.
В ряде случаев оказывается, что после первого этапа расчета могут быть две точки потокораздела: одна по активной, другая по реактивной мощности (рисунок 10.4а).

Рисунок 10.4
Точка 2 – точка потокораздела для активной мощности, а точка 3 – для реактивной мощности. В этом случае кольцевая сеть также условно разрезается по точкам потокораздела и представляется двумя разомкнутыми линиями (рисунок 10.4б).
В этом случае определяются потери мощности на участке между точками потокораздела
DР 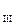 =
=  ,
,
DQ 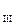 =
=  .
.
Нагрузку в точке 2 принимаем равной
 =Р
=Р  + jQ
+ jQ  =P
=P  + j(Q
+ j(Q  +DQ
+DQ 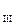 ),
),
в точке 3
 =Р
=Р  + jQ
+ jQ  = P
= P  + DP
+ DP 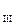 + jQ
+ jQ  .
.
Далее расчет ведем как для двух разомкнутых линий.
При выполнении предварительных расчетов, т.е. когда неизвестны сечения проводов, задаются условием равенства сечения проводов на всех участках сети. В этом случае отношение  =const и расчет можно проводить по длине участков. При этом формулы (10.7) будут иметь вид.
=const и расчет можно проводить по длине участков. При этом формулы (10.7) будут иметь вид.
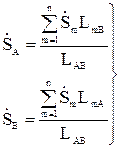 (10.8)
(10.8)
Лекция 11
11.1 Расчеты режима линий с двусторонним питанием при различающихся напряжениях источников питания.
Линия с двусторонним питанием при различающихся напряжениях по концам относится к числу электрических цепей с независимыми источниками мощности. Для расчета таких линий используется принцип наложения.
На рисунке 11.1 приведена исходная схема линии с двусторонним питанием (а) при U  ¹U
¹U  , а также две схемы, полученные в соответствии с принципом наложения (б,в). При этом в напряжении на шинах В выделены две составляющие, одна из которых равна напряжению на шинах А, т.е.
, а также две схемы, полученные в соответствии с принципом наложения (б,в). При этом в напряжении на шинах В выделены две составляющие, одна из которых равна напряжению на шинах А, т.е.
 =
=  +D
+D  (11.1)
(11.1)

Рисунок 11.1
Токи в исходной схеме рассматриваются как результат суммирования двух систем токов, одна из которых определяется действием напряжений  =
=  при DЕ = 0 (рисунок 11.1б), а другая возникает под действием дополнительной э.д.с DЕ при
при DЕ = 0 (рисунок 11.1б), а другая возникает под действием дополнительной э.д.с DЕ при  =
=  = 0 (рисунок 11.1в). Приведенные схемы позволяют выполнить точные расчеты режима исходной схемы.
= 0 (рисунок 11.1в). Приведенные схемы позволяют выполнить точные расчеты режима исходной схемы.
Если предположить для схемы рисунка 11.1б, что напряжение в точке 1 и 2 равно номинальному, то для расчета этой схемы можно использовать формулы, полученные для кольцевой сети. При расчете схемы рисунка 4.6в нагрузки узловых точек 1 и 2 можно исключить из схемы (токи в ветвях не потекут), а в линии будет протекать только уравнительный ток, вызванный действием подключенной DЕ
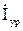 =
= 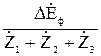 =
=  . (11.2)
. (11.2)
В результате наложения двух расчетов получаем мощности на головных участках линии
 ,
,
 .
.
В общем случае при n нагрузках с учетом (11.2) эти формулы могут быть записаны в виде
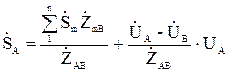 , (11.3)
, (11.3)
 . (11.4)
. (11.4)
Дальнейший расчет заключается в определении точки потокораздела и в определении напряжений в узловых точках, так же как и в кольцевых сетях.
Лекция 12
12.1 Расчет сложно-замкнутых сетей методом преобразования сети.
В ряде случаев при проектировании, а также при эксплуатации сетей небольшой сложности возникает необходимость проведения одноразовых расчетов без применения ПЭВМ, одним из распространенных способов ручного счета – последовательное упрощение схемы сложной сети по методу преобразования сети.
Сущность метода преобразования заключается в том, что заданную сложную сеть путем постепенных преобразований приводят к линии с двусторонним питанием, в которой распределение мощностей находят уже известным методом. Затем, после определения линейных мощностей на каждом участке преобразованной схемы, с помощью последовательных обратных преобразований находят действительное распределение мощностей в исходной схеме сети.
Эквивалентирование параллельных линии на любых участках замкнутой сети возможно только в том случае, если на этих линиях нет присоединенных нагрузок. Для участка замкнутой сети с двумя параллельными линиями (рисунок 12.1)
 =
=  +
+  ;
;  .
.
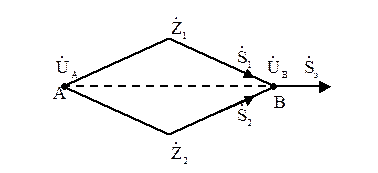
Рисунок 12.1
Если в схеме существуют промежуточные нагрузки, то эквивалентирование осуществить нельзя. Для этого делают так называемый перенос нагрузок в другие точки сети. При этом режим сети до переноса и после должен оставаться неизменным.
Вывод зависимостей, определяющих величины переменных нагрузок, можно сделать для общего случая, когда между точками сети, в которые требуется перенести нагрузку, имеется несколько потребителей энергии (рисунок 12.2).
 Рисунок 12.2
Рисунок 12.2
Рассматривая сеть как линию с двусторонним питанием и принимая напряжения во всех узлах одинаковыми по величине и фазе в соответствии с (10.7), определим мощности, вытекающие из точек А и В
 =
=  , (12.1)
, (12.1)
 =
=  . (12.2)
. (12.2)
Если перенести нагрузку  в точки А и В, то схема участка сети примет вид (рисунок 12.2б), а мощности
в точки А и В, то схема участка сети примет вид (рисунок 12.2б), а мощности  и
и  определяются
определяются
 =
=  , (12.3)
, (12.3)
 =
=  , (12.4)
, (12.4)
где  =
= 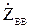 =0.
=0.
Так как применение нагрузок не должно менять режима сети, находящейся за границами рассматриваемого участка, то  =
=  и
и  =
=  . Приравнивая уравнения (12.1) и (12.3), а также (12.2) и (12.4), получим
. Приравнивая уравнения (12.1) и (12.3), а также (12.2) и (12.4), получим
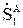 =
=  и
и  =
=  .
.
Аналогично в общем случае для любой промежуточной нагрузки можно найти
 (12.5)
(12.5)
Иногда при расчете сети требуется произвести преобразования треугольника в эквивалентную звезду и обратно (рисунок 12.3).

Рисунок 12.3
Сопротивления лучей эквивалентной звезды определяются
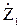 =
=  ;
;  =
= 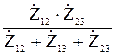 ;
; 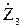 =
= 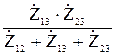 . (12.6)
. (12.6)
Обратные преобразования
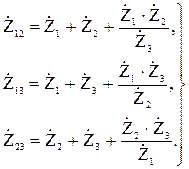 (12.7)
(12.7)
При развертывании преобразований схемы в исходную необходимо найти распределение мощностей на сторонах треугольника по полученному распределению мощностей в лучах эквивалентной звезды.
Примем условно, что в лучах звезды получено распределение мощностей в соответствии с рисунком 12.3. Мощности на сторонах треугольника получаем, исходя из равенства векторов падений напряжения на любой стороне треугольника и смежных ей лучах звезды.
Задавшись направлениями мощностей на сторонах треугольника и определив токи на участках по номинальному напряжению сети, получим
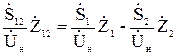 ,
,
откуда
 (12.8)
(12.8)
Если результат получится с отрицательным знаком, то условно принятое направление мощности на этой стороне треугольника следует изменить на обратное.
Дата добавления: 2015-01-29; просмотров: 1925; Мы поможем в написании вашей работы!; Нарушение авторских прав |