Интеграл с переменным верхним пределом

Определение 3. Пусть функция интегрируема по Риману на сегменте . Интегралом с переменным верхним пределом от функции называется функция

.

Пример. Пусть на сегменте рассматривается функция . Поскольку непрерывна на сегменте , она интегрируема по Риману на этом сегменте, а также на любом сегменте . Тогда по предыдущему определению для функции можно определить интеграл с переменным верхним пределом:

.

Определенный интеграл с переменным верхним пределом является функцией, его значение можно вычислить в любой точке сегмента . Для того, чтобы вычислить нужно в интеграл Вместо верхнего переменного предела поставить конкретное значение и вычислить обычный интеграл Римана . Например:

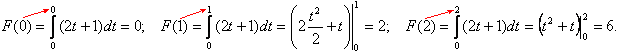
Теорема. Пусть функция интегрируема по Риману на сегменте , тогда функция непрерывна в каждой точке .

Доказательство. Возьмем любые аргументы и рассмотрим .

Пусть сначала :

Поскольку интегрируема по Риману на сегменте , то она ограничена на этом сегменте, т.е.

, что для ,

тогда

. (21)

Рассмотрим теперь случай, когда . Аналогично получим, что здесь имеет место неравенство

. (22)

Объединяя (21) и (22), получим, что для

. (23)

Учитывая (23), имеем:

, что таких, что выполняется:

что означает равномерную непрерывность (по определению равномерной непрерывности), а потому и просто непрерывность в каждой точке .

Теорема. Пусть функция интегрируема по Риману на сегменте и непрерывна в точке , тогда дифференцируема в точке и

.

Замечание. Условие непрерывности функции в точке не является необходимым для дифференцируемости функции в точке .

Пример. Пусть на за исключением конечного количества точек, где . Тогда

для ,

поэтому дифференцируема в каждой точке , хотя имеет устранимые разрывы в конечном количестве точек .

Замечание. Если имеет в точке разрыв І-го рода, то недифференцируема в точке (теорема Дарбу).