
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формализуемые решения
Формализуемые решения принимаются на основе соответствующих математических методов (алгоритмов).
Математическая модель задачи оптимизации формализуемого решения включает следующие элементы:
1. заданную оптимизируемую целевую функцию (критерий управляемости): Ф = F(x1, x2,…,xn), (j = 1, 2,…,n) , где xj - параметры, учитываемые при принятии решения (отражающие ресурсы принятия решений);
2. условия, отражающие ограниченность ресурсов и действий при принятии решений: gi(xj) < ai, ki (xj) = bi; cj < xj < di, i = 1, 2,…,m; j = 1, 2,…, n.
Непременным требованием для решения задачи оптимизации является условие n > m.
В зависимости от критерия эффективности, стратегий и факторов управления выбирается тот или иной метод (алгоритм) оптимизации.
Основными являются следующие классы методов:
1. методы линейного и динамического программирования (принятия решения об оптимальном распределении ресурсов);
2. методы теории массового обслуживания (принятие решения в системе со случайным характером поступления и обслуживания заявок на ресурсы);
3. методы имитационного моделирования (принятие решения путем проигрывания различных ситуаций, анализа откликов системы на различные наборы задаваемых ресурсов);
4. методы теории игр (принятие решений с помощью определения стратегии в тех или иных состязательных задачах);
5. методы теории расписаний (принятие решений с помощью разработки календарных расписаний выполнения работ и использования ресурсов);
6. методы сетевого планирования и управления (принятие решений с помощью оценки и перераспределения ресурсов при выполнении проектов, изображаемых сетевыми графиками);
7. методы многокритериальной (векторной) оптимизации (принятие решений при условии существования многих критериев оптимальности решения) и др.
Выбор решения - заключительный и наиболее ответственный этап процесса принятия решений.
Здесь необходимо осмыслить всю информацию, полученную на этапах постановки задачи и формирования решений и использовать ее для обоснования выбора решения. В реальных задачах принятия решений к началу этапа выбора решения еще сохраняется большая неопределенность, поэтому сразу осуществить выбор единственного решения из множества допустимых решений очень сложно.
Поэтому на практике используется принцип последовательного уменьшения неопределенности, который заключается в последовательном трехэтапном (обычно) сужении множества решений:
· На первом этапе исходное множество альтернативных решений Y сужается (используя ограничения на ресурсы) до множества приемлемых или допустимых решений Y1  Y.
Y.
· На втором этапе множество допустимых решений Y1 сужается (учитывая критерий оптимальности) до множества эффективных решений Y2  Y1.
Y1.
· На третьем этапе осуществляется выбор (на основе критерия выбора и дополнительной информации, в том числе и экспертной) единственного решения Y*  Y2.
Y2.
Система принятия решений – это совокупность организационных, методических, программно-технических, информационно-логических и технологических обеспечений принятия решений для достижения поставленных целей.
Общая процедура принятия решений может состоять из следующих этапов:
· анализ проблемы и среды (цели принятия решения, их приоритеты, глубина и ограничения рассмотрения, элементы, связи, ресурсы среды, критерии оценки);
· постановка задачи (определение спецификаций задачи, альтернатив и критериев выбора решения);
· выбор (адаптация, разработка) метода решения задачи;
· выбор (адаптация, разработка) метода оценки решения;
· решение задачи (математическая и компьютерная обработка данных, имитационные и экспертные оценки, уточнение и модификация, если это необходимо);
· анализ и интерпретация результатов.
Задачи принятия решений могут быть поставлены и решены в условиях:
· детерминированности, т.е. определенности, формализуемости и единственности целевой функции, детерминированности риска, когда возможные решения, исходы распределены вероятностно;
· недетерминированности, т.е. неопределенности, неточности, плохой формализуемости информации.
В моделях принятия решений используются различные процедуры. В частности, наиболее просты и эффективны следующие:
· методы математического программирования;
· методы кривых безразличия;
· многокритериального выбора альтернатив на основе четкого или же нечеткого отношения предпочтения;
· последовательной оценки и последующего исключения вариантов;
· многомерного ранжирования объектов и др.
При выборе рационального решения необходимо принимать во внимание внешнюю среду и побочные явления, динамическую изменчивость критериев оценок решения, необходимость ранжирования аспектов и приоритетов решения, их неполноту и разнородность (а иногда и конфликтность).
Продемонстрируем ситуационное моделирование на примере моделирования деятельности банка. Банковская система является одной из подсистем современной экономической системы, наиболее подверженной информатизации.
Развитие банковской системы сопровождается постоянным поиском адекватных оптимальных методов и инструментов управления, принятия решений на основе экономико-математического анализа и моделирования деятельности банков.
При этом необходимо учитывать тот факт, что финансовые операции имеют еще и стохастические составляющие, усложняющие и без того сложные процессы начисления процентных ставок, взносов и выплат, регулирования и управления, инвестиций и др.
Эти процессы сложны не только динамически, но и, логически. Кроме того, от таких прогнозов зависят:
· прогноз,
· анализ темпов инфляции,
· структуры активов и пассивов банка,
· доходности акций,
· курсов валют,
· процентная ставка и др.
Ситуационный анализ денежных потоков является динамическим процессом, использующим методы оптимизации и критерии оптимальности. При ситуационном анализе некоторых базовых значений величины активов можно по некоторым критериям оптимальности выбрать оптимальный набор возможных, допустимых финансовых операций, обеспечивающих, например, наибольшую доходность.
Возможно также получение решения задач, свидетельствующего об отсутствии роста (или малого роста) каких-либо финансовых параметров, например, активов, из которого можно сделать вывод о невозможности проведения оптимизирующих операций (процедур).
Пусть dt - средний уровень доходности, получаемый в результате проведения некоторых инвестиционных мероприятий, а Pt - процентная ставка на момент времени t = 0, 1, 2, ..., T. Тогда рост активов A будет осуществляться по закону
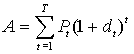
и можно использовать при ситуационном анализе критерий эффективности:

Соотношение между доходностью активов и ценой пассивов коммерческого банка является важнейшим показателем, который отражает эффективность денежно-финансовой политики банка.
Ситуационный анализ соотношения осложняется рядом факторов:
1. Структура активов и пассивов могут отражаться ссудами различной длительности, а также различными схемами размещения и привлечения обязательств и ценных бумаг, например, возврат денег может быть осуществлен по схеме ежемесячного отчисления процентов и уплаты кредита в конце либо по схеме единовременного возврата суммы долга и процентов в конце промежутка кредитования.
2. Необходимостью учета (прогноза) инфляционного ожидания и "увеличения" или "очистки" тех или иных составляющих активов и пассивов в зависимости от инфляции;
3. Различными параметрами и факторами, влияющими на степень риска, затрудненностью оценки величины риска.
Различные структуры и схемы размещения и привлечения финансовых ресурсов определяют и различные динамические модели.
Например, если схема предусматривает возврат долга с процентами одновременно, реальная ставка рублевого кредита d может быть определена по формуле
d = (z - a) / (1 + a / 100) (%),
где z - номинальная ставка рублевого кредита (%), а - инфляция за период кредитования (%).
Одним из эффективных механизмов принятия деловых решений является использование ИСПР (просто СПР) - информационных систем поддержки решений (Decision Support Systems), сочетающих современные средства аналитической обработки и средства визуализации информации и технологии поддержки деятельности экспертной группы.
Литература
1. Казиев В.М. Введение в анализ, синтез и моделирование систем. htpp://www.intuit.ru
2. http://www.fmi.asf.ru/Library/Book/SimModel/Glava1.HTML
Дата добавления: 2015-01-29; просмотров: 230; Мы поможем в написании вашей работы!; Нарушение авторских прав |