
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 2 – Работа Джеймса Клерка Максвелла
Заложивших основу ТАР
«О регуляторах» (1868)

J.C.Maxwell (1831 - 1879)
J.C.Maxwell. On Gavernos. Proceedings of the Royal Society of London. Vol.16, 1868.
В 1868 году появилась работа знаменитого английского физика Д.К. Максвелла «О регуляторах», ставшая одной из основ теории автоматических систем управления. Прежде всего, Максвелл разделил все устройства для регулирования частоты вращения машины на две категории: модераторы и собственно регуляторы. К модераторам он отнес регулирующие устройства, которые в принципе не в состоянии были идеально поддерживать постоянной частоту вращения во всем диапазоне изменения нагрузки (помимо наиболее распространенного на тот период обычного регулятора Уатта, к этой категории были отнесены фрикционный регулятор Д.Эри, водяной регулятор Джона Томсона и др.).
Примечание. Дж.Эри (G.Airy, 1801 - 1892) – английский астроном, математик и изобретатель, первым попытался с помощью математики объяснить явление самораскачивания системы «машина-регулятор». Изобретатель катаракта - особого устройства, порождающего вязкое трение в регуляторе.
К собственно регуляторам Максвелл отнес устройства, способные сводить к нулю любые отклонения частоты вращения от заданного значения. Таким устройством являлся в первую очередь фрикционный регулятор Флеминга Дженкина (условная принципиальная схема управления частотой вращения паровой машины с помощью регулятора Дженкина представлена на рисунке 2.1).
Примечание. В то время существовали и другие астатические регуляторы, например, астатический регулятор Уатта, жидкостный регулятор Вильгельма Сименса …, однако выбор Максвелла пал на регулятор Дженкина.
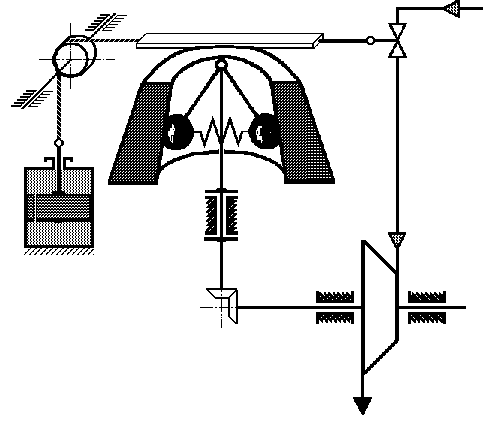
Рисунок 2.1 - Условная принципиальная схема регулирования
частоты вращения паровой машины с помощью регулятора Дженкина
Максвелл убедился, что в системе «машина-регулятор» инерция регулятора не позволяет ему точно следить за ходом машины. Выяснив, что система машина - регулятор имеет полторы степени свободы и, заменив сложные зависимости между переменными в уравнениях движения пропорциональными отношениями (в современной терминологии такой подход называется линеаризацией), он получил следующие уравнения динамики
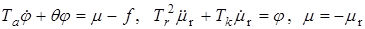 (2.1)
(2.1)
где: 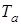 - положительный коэффициент, характеризующий инерционные свойства объекта регулирования, с;
- положительный коэффициент, характеризующий инерционные свойства объекта регулирования, с; 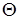 - вещественный коэффициент, характеризующий свойство саморегулируемости объекта;
- вещественный коэффициент, характеризующий свойство саморегулируемости объекта; 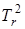 - положительный коэффициент, характеризующий инерционные свойства регулятора, с2;
- положительный коэффициент, характеризующий инерционные свойства регулятора, с2; 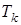 - положительный коэффициент, характеризующий величину вязкого трения в регуляторе, с;
- положительный коэффициент, характеризующий величину вязкого трения в регуляторе, с; 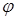 - регулируемая переменная (относительное изменение частоты вращения);
- регулируемая переменная (относительное изменение частоты вращения); 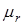 - регулирующее воздействие (относительное перемещение регулятора);
- регулирующее воздействие (относительное перемещение регулятора); 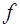 - возмущающее воздействие - величина, характеризующая относительное изменение нагрузки;
- возмущающее воздействие - величина, характеризующая относительное изменение нагрузки; 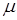 - относительное открытие паровпускного клапана;
- относительное открытие паровпускного клапана; 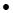 - символ дифференцирования по времени
- символ дифференцирования по времени 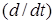 ,
, 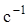 . При этом первое уравнение в (2.1) определяет динамику машины-двигателя, второе - динамику регулятора.
. При этом первое уравнение в (2.1) определяет динамику машины-двигателя, второе - динамику регулятора.
Примечание. Отмечать производные точкой (например: 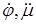 и т.д.) предложил И.Ньютон (Isaac Newton, 1643 - 1727), отмечать производную штрихом (например:
и т.д.) предложил И.Ньютон (Isaac Newton, 1643 - 1727), отмечать производную штрихом (например: 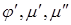 и т.д.) предложил Лагранж (Joseph Louis Lagrange, 1736 - 1813), отмечать производную в виде
и т.д.) предложил Лагранж (Joseph Louis Lagrange, 1736 - 1813), отмечать производную в виде 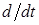 (например:
(например: 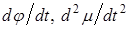 и т.д.) предложил Коши (Augustin Cauchy, 1789 - 1857).
и т.д.) предложил Коши (Augustin Cauchy, 1789 - 1857).
Уравнения (2.1) можно наглядно представить в виде, так называемой, структурной математической модели (представлено на рисунке 2.2).
На структурной схеме отображены взаимосвязи, существующие между переменными, как внутри объекта регулирования (машины) и автоматического устройства (регулятора), так и между ними, а также внешнее воздействие 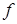 и начальные отклонения (условия) по переменным состояния
и начальные отклонения (условия) по переменным состояния 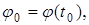
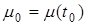 ,
, 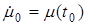 . Где
. Где 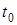 - исходное (начальное) значение независимой переменной
- исходное (начальное) значение независимой переменной  .
.
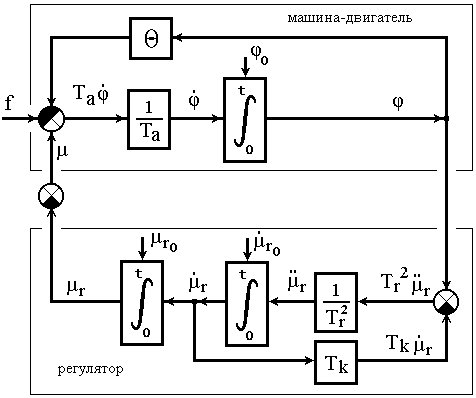
Рисунок 2.2 - Структурная математическая модель системы:
машина-двигатель, управляемая астатическим регулятором
Таким образом, работа регулятора совместно с машиной-двигателем могла быть рассмотрена с позиций малых колебаний каких-либо переменных относительно стационарного состояния (состояния равновесия), что позволяло применить для описания динамики более простой и доступный математический аппарат - теорию линейных дифференциальных уравнений.
При совместном решении уравнений (2.1), например, относительно 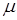 динамика (движения) системы «машина-астатический регулятор» описывается линейным дифференциальным уравнением третьего порядка.
динамика (движения) системы «машина-астатический регулятор» описывается линейным дифференциальным уравнением третьего порядка.
Уравнение динамики, относительно переменной 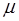 :
:
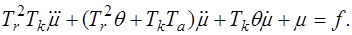 (2.2)
(2.2)
В структурном виде (в виде структурной математической модели) уравнение (2.2) представлено на рисунке 2.3.
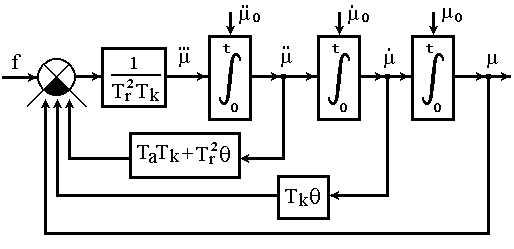
Рисунок 2.3 - Структурная математическая модель системы:
машина-двигатель, управляемая астатическим регулятором
Движения в системе ( 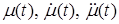 ) возникают при, хотя бы одном, ненулевом возмущении, к которым относятся начальные отклонения (
) возникают при, хотя бы одном, ненулевом возмущении, к которым относятся начальные отклонения ( 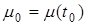 ,
, 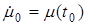 ,
, 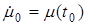 ) и внешнее воздействие
) и внешнее воздействие 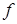 (смотри рисунок 2.3). Движения, возникающие при
(смотри рисунок 2.3). Движения, возникающие при 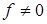 , называются возмущенными движениями. Движения, возникающие при ненулевых начальных отклонениях (
, называются возмущенными движениями. Движения, возникающие при ненулевых начальных отклонениях ( 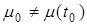 ,
, 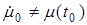 , …) называются собственными.
, …) называются собственными.
Примечание. Уравнения равновесия (уравнения статики) легко получаются из соответствующих уравнений динамики приравниванием нулю всех производных в уравнениях динамики.
Характеристическое уравнение уравнений (2.1), (2.2) и (2.3) определяется выражением:
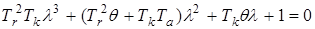 , (2.4)
, (2.4)
где 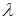 - корень уравнения (размерность корня -
- корень уравнения (размерность корня - 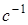 ).
).
Характеристическое уравнение (2.4) можно легко получить из уравнений (2.2) и (2.3) приравниванием правых частей уравнений нулю и заменой в левых частях 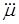 на
на 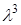 ,
,  - на
- на 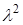 ,
,  - на
- на 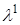 и
и 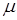 - на
- на 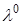 .
.
За условие устойчивости системы впервые было принято условие отрицательности корней (отрицательности вещественных частей корней) уравнения (2.4).
Таким условием стало следующее неравенство (условие Максвелла):
 . (2.5)
. (2.5)
Примечание. Условие (2.5) легко получить с помощью несложного правила: произведение средних коэффициентов в уравнении (2.4) должно быть больше произведения крайних.
Максвелл показал, что математический метод описания динамики системы «машина-регулятор» линейным дифференциальным уравнением третьего порядка, сводящий исследование устойчивости системы к нахождению условий отрицательности корней алгебраического уравнения третьей степени, позволяет понять механизм возникновения неустойчивости работы машины.
Дата добавления: 2015-01-29; просмотров: 198; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Вопрос 3. Механизм составления промежуточного и окончательного ликвидационного баланса | | | ВВЕДЕНИЕ. «Для того, чтобы понять, что такое маркетинг, достаточно одного часа |