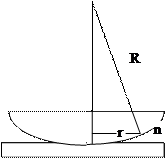
Кольца Ньютона

Кольца Ньютона – пример полос равной толщины, наблюдаемых при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 8).

Тогда радиусы темных колец Ньютона в отраженном свете , (50) а радиусы светлых колец Ньютона в отраженном свете

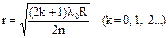. (51)

Здесь R – радиус кривизны линзы, n – показатель преломления вещества между линзой и пластинкой.

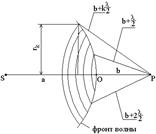
11. Принцип Гюйгенса-Френеля. Метод зон Френеля.Дифракцией называется огибание волной препятствий. Дифракция выражена достаточно сильно, если длина волны соизмерима с размерами препятствия. Возникновение дифракции можно объяснить с помощью принципа Гюйгенса: каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент. Для количественной оценки результатов дифракции и нахождения амплитуды результирующей волны в любой точке пространства Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции. дифракции Френель предложил разбивать фронт волны не на бесконечное множество точечных источников, а на конечное число зон. Зонами Френеля называются участки фронта волны, построенные таким образом, что расстояние от краев каждой зоны до точки наблюдения отличаются на l/2. длина волны света/2. объясняет прямолинейность распространения света в свободной от препятствий однородной среде.

Колебания, приходящие в точку наблюдения P от аналогичных точек двух соседних зон, будут находиться в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на p.

Радиус внешней границы k-ой зоны Френеля в этом случае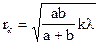

где а – расстояние от источника света до фронта волны, b – расстояние от точки наблюдения до вершины фронта волны О.

Для плоской волны радиус находится как .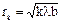

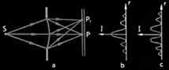
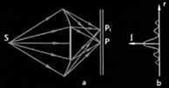
12, Дифракция Френеля на круглом отверстии и диске.Зонами Френеля называются участки фронта волны, построенные таким образом, что расстояние от краев каждой зоны до точки наблюдения отличаются на l/2. длина волны света/2. Для качественной оценки результата дифракции на малом круглом отверстии достаточно найти количество зон Френеля, попавших в это отверстие. Если количество зон четное, то в точке Р будет минимум, если нечетное – максимум.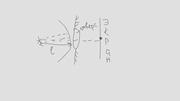

d- отверстие

l=d в квадрате/лямбду(длину волны света) l- расстояние от источника до отверстия.

на круглом отверстии и

на круглом диске.

Если открыто ровно m первых зон Френеля, то амплитуда в точке P равна A=A₁-A₂+...±A_m.

Если m нечетное число, то эта формула преобразуется в следующую A=A₁/2+A_m/2, и в точке P поле усиливается, интенсивность I имеет максимум (b). r- расстояние на экране, отложенное от точки P.

Если m четное число, то A=A₁/2-A_m/2 , и в точке P получается темное пятно

Если закрыть m первых зон Френеля, то амплитуда в точке P будет равна

A=A_m+1-A_m+2-...=A_m+1/2+(A_m+1/2-A_m+2+A_m+3/2)+...=A_m+1/2 .

Таким образом, в центре геометрической тени, в точке P будет светлое пятно

14. Дифракция Фраунгофера на дифракционной решетке.Большое практическое значение имеет дифракция Фраунгофера на так называемой дифракционной решетке. Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние, щелей

Расстояние d между серединами соседних щелей называется постоянной или периодом решетки. При этом в направлениях, для которых разность хода волн от соседних щелей равна целому числу длин волн, будут наблюдаться максимумы интенсивности, называемые главными. Таким образом, условие главных максимумов имеет вид

dsinj = 2kl/2, k = 0, 1, 2...

При этом интенсивность главных максимумов I_max пропорциональна интенсивности I_j , создаваемой в направлении j одной щелью. I_max = N²I ,

где N – общее число щелей решетки.

Дифракционная решетка служит спектральным прибором, разрешающая способность которого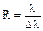

где Dl – наименьшая разность длин волн двух близких спектральных линий с длинами волн l и l+Dl, при которых они еще воспринимаются раздельно (разрешаются).

Разрешающая способность дифракционной решетки может быть найдена по формуле

R=kN,

где k – порядок дифракционного спектра, N – общее число щелей решетки.

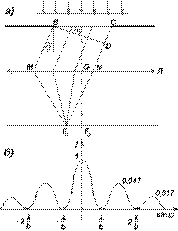
13. Дифракция Фраунгофера на одной щели.параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана узкая щель ВС, имеющая постоянную ширину b и длину l>>b Оптическая разность хода между крайними лучами ВМ и CN, идущими от щели под углом j к оптической оси линзы OF₀ D=CD=bsinj.Разобьем щель ВСна зоны Френеля, имеющие вид полос, параллельных ребру Вщели. Ширина каждой зоны выбирается (согласно методу зон Френеля) так, чтобы разность хода от кПри интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами.Всего на ширине щели уместится D:

l/2= bsinj/(l/2) зон. Если число зон четное, т.е.

bsinj/(l / 2)=± 2mили bsinj=± ml , m=1,2,3-,

то наблюдается дифракционный минимум (темная полоса).Если число зон нечетное, т.е.

bsinj/(l / 2)= ± (2m+1)или bsinj= ± (2m+1) 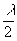, m=1,2,3-,

то наблюдается дифракционный максимум (светлая полоса).

раев этих зон была равна l/2.Углы, под которыми наблюдаются максимумы всех порядков, начиная с первого, зависят от длины волны света l. Поэтому, если щель освещать немонохроматическим светом, то максимумы, соответствующие разным длинам волн, будут наблюдаться под разными углами и, следовательно, будут пространственно разделены на экране. Получим дифракционный спектр, в отличие от призматического спектра