Соотношение неопределенностей

Своеобразие свойств микрочастиц проявляется в том, что не для всех динамических переменных, характеризующих состояние микрочастицы, получаются при измерениях определенные значения. Так, например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и компоненты импульса р_x. Неопределенности значений x и р_х удовлетворяют соотношению

.

Из этого следует, что чем меньше неопределенность одной из переменных (х или P_x), тем больше неопределенность другой.

Соотношение, аналогичное ) имеет место для y и р_y, для z и p_z, а также для ряда других пар величин, называемых канонически сопряженными.

Например, энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей

.

Это соотношение означает, что определение энергии с точностью DЕ должно занять интервал времени Dt, не меньший, чем определяемый соотношением .

23. Волновая функция. Уравнение Шредингера.Состояние микрочастицы в квантовой механике характеризуется так называемой волновой функцией, обозначаемой буквой Y (пси). Вид этой функции получается из решения уравнения Шредингера, которое выглядит следующим образом:

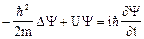. (26)

Здесь m - масса частицы, U – ее потенциальная энергия, i – мнимая единица,

D – оператор Лапласа, Y = Y(x,y,z,t) – функция координат и времени.

.

Если силовое поле, в котором движется частица, стационарно, т.е. U не зависит явно от времени, то уравнение переходит в более простое уравнение Шредингера для стационарных состояний:

.

Здесь Y = Y(x,y,z) – функция координат.

Согласно Борну квадрат модуля волновой функции дает плотность вероятности нахождения частицы в соответствующем месте пространства.

.

В соответствии с этим для волновой функции должно выполняться условие нормировки

.

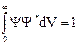В соответствии со своим смыслом волновая функция должна быть однозначной, конечной, непрерывной и иметь непрерывную и конечную производную. Совокупность этих требований носит название стандартных условий.

Уравнение Шредингера имеет решения, удовлетворяющие стандартным условиям, лишь при некоторых избранных значениях параметра Е (т.е. энергии). Эти избранные значения называются собственными значениями энергии. Решения, соответствующие собственным значениям Е, называются собственными функциями частицы. Совокупность собственных значений называется энергетическим спектром. Он может быть дискретным или сплошным. В случае дискретного спектра собственные значения.

24. Модели атома Ререрфорда. модель Резерфорда — историческая модель строения атома, которую предложил Резерфорд в результате эксперимента с рассеиванием альфа-частиц. По этой модели атом состоит из небольшого положительно заряженного ядра, в котором сосредоточена почти вся масса атома, вокруг которого движутся электроны, — подобно тому, как планеты движутся вокруг Солнца. ОПЫТ

изучая прохождение альфа-частиц через тонкие листики фольги, оказалось, что большинство частиц проходят через фольгу, не изменяя направления своего движения. следовательно атом это не сплошь заполненный каким либо веществом объем. Лишь малая часть объема атома препятствует прохождению альфа частиц и вызывает ее отклонение от прямолинейного пути, этот малый объем и есть ядро атома. Он подсчитал число частиц, испытавших большое отклонение, смог определить размеры атомного ядра и смог доказать, что в этом малом объеме сосредоточена вся масса атома.

Fц- центроб. силы у электрона

Fгр- гравитационные силы ел

и они равны!

25. Постулаты Бора.

Теория атома, предложенная Н. Бором, основана на двух постулатах.

1. Электрон в атоме может находиться только в одном из дискретных стационарных состояний, и имеет кратный момент импульса.

При этом излучение и поглощение энергии не происходит.

2. Излучение испускается или поглощается в виде светового кванта энергии при переходе электрона из одного стационарного состояния в другое. Энергия светового кванта равна разности энергий тех стационарных состояний, между которыми совершается квантовый скачок электрона:

.

Применение этих постулатов для расчета параметров атома водорода позволило найти:

1) радиусы стационарных орбит ;

2) cкорости движения электрона на этих орбитах ;

3) энергии стационарных состояний атомов ;

4) длины волн спектральных линий, возникающих при переходах электрона из одного стационарного состояния (с номером n₁) в другое (с номером n₂):

,

26. Сектор атома водорода по Бору Используя законы механики Ньютона и правило квантования, на основе которого определяются возможные стационарные состояния атома. Бор смог вычислить радиусы орбит электрона и энергии стационарных состояний атома. Минимальный радиус орбиты определяет размеры атома. На рисунке значения энергий стационарных состояний (в элекгрон-вольтах¹) отложены на вертикальной оси.

Второй постулат Бора позволяет вычислить по известным значениям энергий стационарных состояний частоты излучений атома водорода.
энергию принято выражать в электронвольтах (сокращенно эВ). 1 эВ равен энергии, приобретаемой электроном при прохождении им разности потенциалов 1 В: 1 эВ = 1,6 . 10 Дж.

Теория Бора приводит к количественному согласию с экспериментом для значений этих частот. Все частоты излучений атома водорода составляют в своей совокупности ряд серий, каждая из которых образуется при переходах атома в одно из энергетических состояний со всех верхних энергетических состоянийПереходы в первое возбужденное состояние (на второй энергетический уровень) с верхних уровней образуют серию Бальмера. На рисунке 12.4 эти переходы изображены стрелками. Красная, зеленая и две синие линии в видимой части спектра водорода (см. рис. V, 3 на цветной вклейке) соответствуют переходам