ТЕОРИЯ ПРЕДЕЛОВ

ТЕОРИЯ ПРЕДЕЛОВ

Вариант №17

1.Доказать, что . Найти такой номер N(e), начиная с которого члены последовательности отличаются от 4/3 не более чем на e=0,001.

2.Вычислить пределы числовых последовательностей:

а)	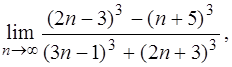б)
в)	г)

3. Вычислить пределы функций:

а)	б) ,
в)	г) ,
д) ,	е) .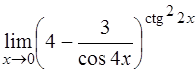

4. Вычислить односторонние пределы:

.

5.Построить график и определить характер точек разрыва:

Типовой расчет по теме:

ТЕОРИЯ ПРЕДЕЛОВ

Вариант №18

1.Доказать, что . Найти такой номер N(e), начиная с которого члены последовательности отличаются от 3/2 не более чем на e=0,005.

2.Вычислить пределы числовых последовательностей:

а)	б)
в)	г)

3. Вычислить пределы функций:

а)	б) ,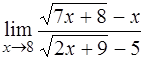
в)	г) ,
д) ,	е) .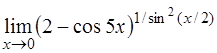

4. Вычислить односторонние пределы:

.

5.Построить график и определить характер точек разрыва:

Типовой расчет по теме:

ТЕОРИЯ ПРЕДЕЛОВ

Вариант №19

1.Доказать, что 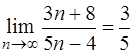. Найти такой номер N(e), начиная с которого члены последовательности отличаются от 3/5 не более чем на e=0,001.

2.Вычислить пределы числовых последовательностей:

а)	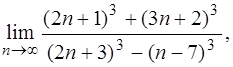б)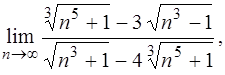
в)	г)

3. Вычислить пределы функций:

а)	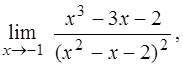б) ,
в)	г) ,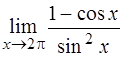
д) ,	е) .

4. Вычислить односторонние пределы:

.

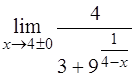5.Построить график и определить характер точек разрыва:

Типовой расчет по теме:

ТЕОРИЯ ПРЕДЕЛОВ

Вариант №20

1.Доказать, что . Найти такой номер N(e), начиная с которого члены последовательности отличаются от 1/2 не более чем на e=0,005.

2.Вычислить пределы числовых последовательностей:

а)	б)
в) 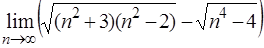,	г) .

3. Вычислить пределы функций:

а)	б) ,
в)	г) ,
д) ,	е) .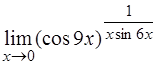

4. Вычислить односторонние пределы:

.

5.Построить график и определить характер точек разрыва:

Типовой расчет по теме:

Дата добавления: 2015-01-29; просмотров: 13; Нарушение авторских прав