Статистическое моделирование на ЭВМ; (Китаев Вячеслав)

Статистическое моделирование представляет собой метод получения с помощью ЭВМ статистически данных о процессах, происходящих в моделируемой системе.

Сущность метода статистического моделирования сводится к построению для процесса функционирования исследуемой системы S некоторого моделирующего алгоритма, имитирующего поведение и взаимодействие элементов системы с учетом случайных входных воздействий и воздействий внешней среды E, и реализации этого алгоритма с использованием программно-технических средств ЭВМ.

Метод применяется:

1) для изучения стохастических систем;

2) для решения детерминированных задач.

Особенностью применения метода заключается во втором методе. А именно замена детерминированной задачи эквива­лентной схемой некоторой стохастической системы, выходные хара­ктеристики последней совпадают с результатом решения детерми­нированной задачи.

В результате статистического моделирования системы S получа­ется серия частных значений искомых величин или функций, стати­стическая обработка которых позволяет получить сведения о пове­дении реального объекта или процесса в произвольные моменты времени. Если количество реализации N достаточно велико, то полученные результаты моделирования системы приобретают ста­тистическую устойчивость и с достаточной точностью могут быть приняты в качестве оценок искомых характеристик процесса функ­ционирования системы S.

Теоретической основой метода статистического моделирования систем на ЭВМ являются предельные теоремы теории вероятностей. Множества случайных явлений (событий, величин) подчиняются определенным закономерностям, позволя­ющим не только прогнозировать их поведение, но и количественно оценить некото­рые средние их характеристики, проявляющие определенную устойчивость.

Примеры статистического моделирования. Методом статистического моделирования найти оценки выходных характеристик стохастической системы S_R., функционирование которой описывается следующими соотно­шениями:

- входное воздействие;

- воздействие внешней среды;

l и j - случайные величины, для которых известны функции распределения.

Целью моделирования является оценка математического ожидания М[у] величины

В качестве оценки математического ожидания М [у], как следует из приведенных теорем теории вероятностей, может выступать среднее арифметическое, вычисленное по формуле

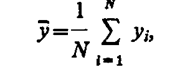
где y_i — случайное значение величины у; N — число реализации мат. ожиданий, которое достаточно для статистической устойчивости результатов.

Структурная схема системыS_R показана на рис. 1.

Рис. 1. Структурная схема систе­мы S_R

Здесь элементы выполняют следующие функции:

вычисление

В_1, В₂ на выходе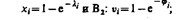

K1 и K2:

суммирование С:

извлечение квадратного корня И

Схема алгоритма, реализующего метод статистического моделирования для оценки М[у] системы S_R, приведена на рис. 2.

Здесь LA и FI — функции распределения случайных величин l и j;

N — задан­ное число реализации;

I=i — номер теку­щей реализации;

LAT = l_I;

FII = j _I;

EXP = e;

MY = М[у] ;

SY =

ВИД [...], ГЕН [...], ВРМ[...]—процедуры ввода исходных данных, генерации псевдослучайных по­следовательностей и выдачи результатов моделирования соответственно.

Таким образом, данная модель позво­ляет получить методом статистического моделирования на ЭВМ статистическую оценку математического ожидания выход­ной характеристики М[у] рассмотренной стохастической системыS_R. Точность и достоверность результатов взаимодей­ствия в основном будут определяться чис­лом реализации N.

Рис. 2. Схема моделирующего ал­горитма системы S_R