Оценка точности и достоверности результатов моделирования; (Китаев Вячеслав)

Обработка результатов имитационных экспериментов принципиально не может дать точных значений (т.к. моделируются случайные процессы, и мы можем их только как-то оценить). Существует некая степень точности результатов - приближение к какому-то истинному значению. И эта степень точности в значительной мере определяется размером выборки (количеством реализаций).

Задача определения такого размера выборки, который позволяет обеспечить желаемый уровень точности и в то же время минимальную стоимость моделирования, весьма трудна, но и весьма важна.

Число испытаний N определяет точность получаемых результатов моделирования. Если необходимо оценить величину случайного параметра Х по результатам моделирования x1, x2, … xn, то за оценку следует брать величину хср. Но из-за случайности хср будет отличаться от истинного значения параметра Х

а если мы зададимся какой-то точностью оценки (назовем ее - e ), то должно выполняться неравенство:

|Х-хср|<e

e - точность оценки величины случайного параметра Х; (половина ширины доверительного интервала)

хср - среднее значение результатов моделирования x1, x2, … xn.

Вероятность того, что данное неравенство выполняется, называют уровнем значимости или доверительной вероятностью:

P(|Х-xср|<e)=a

a - уровень значимости, доверительная вероятность, (1-a) - достоверность.

Это выражение и берется за основу при определении точности результатов статистических испытаний, т.е. результатов имитационных экспериментов.

α и ε - задаем сами.

Определение количества реализаций для оценки вероятности наступления события.

Отклики моделей обычно одно из двух состояний, например успех - неудача. Такие отклики называют переменными Бернулли. Они характеризуются биномиальным распределением.

Пусть целью моделирования будет определение вероятности наступления некоторого события А, определяющего какое-то состояние моделируемой системы. В любой из реализаций процесс наступления события А является случайной величиной, которая может приобретать значение x1=1 с вероятностью р (т.е. событие наступило) и x2=0 с вероятностью 1-р.

На основе центральной предельной теоремы, можно найти количество реализаций для оценки вероятности наступления события с заданным уровнем значимости и точностью.

Центральная предельная теорема: распределение суммы независимых наблюдений n различных СВ стремится к нормальному, при n®Ґ, независимо от характера распределения СВ.

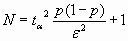
ta - квантиль нормального распределения вероятностей. Находится из специальных таблиц распределения Стьюдента (t-распределение) на основе заданного уровня значимости и определенных степеней свободы.

Число степеней свободы: ν = k - 1 - m, (k - число значений или интервалов СВ; т - число определяемых параметров).

Для определения вероятности р делают пробные испытания (N=50…100) и получают частоту m/N, после чего определяют конечное количество испытаний.

р=m/N

Определение количества реализаций для оценки среднего значения случайной величины.

Случайная величина имеет математическое ожидание m и дисперсию s2.

На основе центральной предельной теоремы количество реализаций N для оценки среднего значения случайной величины будет

Величину σ нужно либо знать, либо для ее определения нужно провести пробный эксперимент и найти ее оценку.

Если мы имеем представление о пределах, в которых может изменяться отклик системы, то грубую оценку величины σ можно получить из условия, что размах переменной отклика равен примерно 4σ: Если известен разумный размах переменной отклика - d, то σ=d/4.

Для определения оценки s2 проводят 50…100 испытаний и определяют по формуле: