Вопрос №11. Прогнозирование на основе рядов динамики

Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени. Для выявления специфики развития изучаемых явлений за отдельные периоды времени определяют абсолютные и относительные показатели изменения ряда динамики: абсолютные приросты, абсолютное значение одного процента прироста, темпы роста и прироста. Выяснение сущности этих показателей, их взаимосвязей, методов расчета – необходимое условие усвоения данной темы.

Рядом динамики называется ряд последовательно расположенных во времени числовых значений соответствующего показателя. Ряд динамики состоит из двух элементов:

1) периода времени, за который или по состоянию на который приводятся числовые значения;

2) числовых значений того или иного показателя, называемых уровнями ряда.

Рассматривая данные показатели, необходимо правильно выбирать базу сравнения, которая зависит от цели исследования. При сравнении каждого уровня ряда с предыдущем получаются цепные показатели; при сравнении каждого уровня с одним и тем же уровнем (базой) получают базисные показатели.

Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост(∆). Его величина определяется как разность двух сравниваемых уровней. Она вычисляется по формуле:

∆_ц = у_i – у_i-1 или ∆_б = у_i – у₀,

где у_i – уровень i-го года;

у₀ – уровень базисного года.

Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному, которое всегда представляет собой положительное число. Этот показатель принято называть темпом роста (Т_р). Он выражается в процентах, т.е.

Т_р = у_i/у_i-1 × 100 или Т_р = у_i/у₀ × 100.

Темп роста может быть выражен и в виде коэффициента (К_р). В этом случае он показывает, во сколько раз данный уровень ряда больше уровня базисного года или какую его часть он составляет.

Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Т_пр), который рассчитывается как отношение абсолютного прироста к предыдущему или базисному уровню, т.е.

Т_пр = ∆/у_i-1 × 100 или Т_пр = ∆/у₀ × 100.

Темп прироста может быть вычислен также путем вычитания из темпов роста 100%, т.е. Т_пр = Т_р – 100.

Показатель абсолютного значения одного процента прироста (|%|) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах, т.е. |%| = ∆/Т_пр или 0,01 ×у_i-1. Расчет этого показателя имеет экономический смысл только на основе цепных характеристик.

Особое внимание следует уделять методам расчета средних показателей рядов динамики, которые являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики. Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста.

Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.

В интервальном ряду динамики с равноотстоящими уровнями во времени расчет среднего уровня ряда (уˉ) производится по формуле средней арифметическойпростой:

ў = Σу/n.

Если интервальный ряд динамики имеет неравноотстоящие уровни, то средний уровень ряда вычисляется по формуле:

ў = Σ_уt/Σt,

где t – число периодов времени, в течение которых уровень не изменяется.

Для моментного ряда с равноотстоящими уровням средняя хронологическая рассчитывается по формуле:

Ў =(0,5у₁ + у₂ + у₃ +…….+ 0,5у_n ) / (n – 1),

где n – число уровней ряда.

Средняя хронологическая для разноотстоящих уровнеймоментного ряда динамики вычисляется по формуле:

Ў =[ (у₁ + у₂)t₁ + (у₂ + у₃)t₂ + (у₃ + у₄)t₃ +……+ (у_n-1 + у_n)t_{n-1 ]}/ 2Σt_i

Определение среднего абсолютного прироста производится по цепным абсолютным приростам по формуле:

∆ˉ = Σ∆_ц / n–1 или ∆ˉ = у_n – у₀ / n–1.

Среднегодовой темп роста вычисляется по формуле средней геометрической:

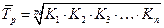, или

где m – число коэффициентов роста.

Существуют специальные таблицы исчисления среднегодовых темпов роста, использование которых позволяет без каких-либо вычислений получить готовые показатели среднегодовых темпов роста и прироста.