Расчет быстротока

В курсовой работе требуется рассчитать конструктивные элементыбыстротока: входную часть, водоскат (лоток) и выходную часть (рисунок 4.3). По расчетным данным построить продольный профиль по оси и план быстротока.

Рекомендуется входную часть запроектировать призматической формы (прямоугольного или трапецеидального сечения) с уклоном дна i = 0 по типу водослива с широким порогом (при P₁ ≥ 0).

Расчет заключается в определении ширины входной части (см. раздел 4.1) и глубины потока в конечном сечении.

Длина входной части принимается в пределах (3-4) Н, а глубина в ее конце – равной критической глубине h_k (см. п. 4.1).

Водоскат быстротока представляет собой лоток из бетона с уклоном дна i > i_k. Следует установить характер кривой свободной поверхности, определить глубину в конце лотка (см. п. 3).

Рекомендуется такая последовательность расчета:

1) По расходу Q и ширине лотка b_л определяется критическая h_k и нормальная h_o глубины. Расчет h_o выполняется по формуле расхода Q = υω с учетом максимально допустимой скорости потока на водоскате υ_доп.

2) По известной h_o и υ_доп из формулы Шези υ = C определяется уклон лотка i_л.

3) По заданной разности отметок 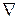ВБ– 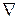НБ, с учетом уклона лотка i_л, определяется длина лотка L.

4) По найденной глубине h_k вычисляют критический уклон i _к.

5) По соотношению уклонов i_л, i_k и глубин h_o, h_k определяется состояние потока в лотке (спокойное, бурное) и характер кривой сводной поверхности.

6) По уравнению неравномерного движения (3.1) выполняется расчет кривой свободной поверхности на водоскате.

Находят расстояние l от начала лотка до места, где устанавливается нормальная глубина h_o. В качестве глубин h₁ и h₂, используемых для определения χ, η₁, η₂, j_ср, φ(η₁), φ(η₂) принимаются глубины в начале и конце лотка (h_k и h_o).

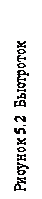
Рисунок 5.3 Схема к расчету неравномерного движения

в лотке быстротока

Найденную длину кривой l сравнивают с длиной L лотка быстротока. Если l < L, неравномерное движение заканчивается в пределах лотка и глубина в конечном сечении h_кон = h_o. Если l > L, неравномерное движение не заканчивается в пределах лотка и глубина h₀ устанавливается за водоскатом. Во втором случае глубину h_кон необходимо определить расчетом. При этом удобно применить метод последовательных приближений, приняв в первом приближении h₂ ≈ h_o. Для детального построения кривой свободной поверхности выполняется расчет промежуточных глубин по длине водоската.

На выходной части быстротока поток из бурного состояния переходит в спокойное с образованием гидравлического прыжка.

Задача расчета состоит в обеспечении полного гашения энергии потока в нижнем бьефе.

Сначала определяется характер сопряжения. При этом глубину в конце водоската h_кон принимают в качестве первой сопряженной глубины и по ней вычисляют вторую сопряженную глубину h″_кон.

Если h″_кон > h_б, в нижнем бьефе проектируется гаситель энергии в виде водобойной стенки или водобойного колодца (см. п.5.1).

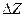- перепад при выходе потока из водобойного колодца в отводящий канал; определяется по рекомендациям (с.494-495 /2/; с.466-467 /3). Для приближенных расчетов величиной 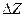можно пренебречь.

Расчет глубины колодца ведется методом последовательных приближений.

Длина водобойного колодца определяется аналогично длине ступеней перепада.

Библиографический список

1. Штеренлихт Д.В. Гидравлика. - М.: КолосС, 2005. - 655 с.

2. Чугаев Р.Р. Гидравлика - М.: БАСТЕТ, 2008. - 672 с.

3. Константинов Н.М., Петров Н.А., Александров В.А. и др. Гидравлика, гидрология, гидрометрия.

М.: Высш. шк., 1987

4. Алмаев Р.А. Гидравлика трубопроводов. –Уфа: Баш ГАУ, 2009. -182 с.

5. Алмаев Р.А. Курс гидравлики в примерах и задачах . –Уфа: Баш ГАУ, 20011. -171 с

6. Большаков В.А., Константинов Ю.М., Попов В.Н. и др. Сборник задач по гидравлике. - Киев:

Выща шк., 1979, - 360 с.

7. Киселёв П.Г. Справочник по гидравлическим расчётам. – М.: Энергия, 1974. - 312 с.

…