
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общие сведения. Полная удельная энергия движущейся жидкости расходуется на преодоление сил трения, возникающих между соседними слоями жидкости и между стенками трубопровода и
Полная удельная энергия движущейся жидкости расходуется на преодоление сил трения, возникающих между соседними слоями жидкости и между стенками трубопровода и пограничным слоем жидкости, а также на преодоление местных сопротивлений. Таким образом, часть механической энергии движущейся жидкости переходит в тепловую и рассеивается в пространстве. Этот процесс необратим. Потери напора необходимо учитывать при расчёте различных гидравлических систем для обеспечения заданных параметров (например, обеспечения требуемого напора воды в системе водоснабжения или необходимого усилия на штоке гидроцилиндра при подъёме кузова автомобиля). В повседневной жизни наиболее часто встречается движение жидкости в круглоцилиндрической трубе, поэтому потери напора при проведении опытов определяются для трубы с некоторым диаметром d.
При установившемся движении жидкости в круглоцилиндрической трубе величина потерь напора по длине зависит от:
- длины трубопровода ℓ и его внутреннего диаметра d, м;
- средней скорости движения жидкости V, м/с;
- абсолютной шероховатости (средней высоты выступов шероховатости) внутренней поверхности трубопровода ∆, мм;
- вязкости жидкости ν, м2/с.
Величину потерь напора по длине вычисляют по формуле Дарси-Вейсбаха:
hдл = λ 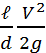 , (2.1)
, (2.1)
| где | λ (ламбда) - безразмерный коэффициент гидравлического трения (коэффициент Дарси). |
Из формулы (2.1) видно, что потери напора по длине hдл пропорциональны квадрату средней скорости потока жидкости V2, длине потока ℓ и обратно пропорциональны геометрическим размерам потока (диаметру d). Коэффициент гидравлического трения λ позволяет приравнять обе части уравнения, поэтому возникает необходимость определения его численного значения.
В общем случае λ = f (Re, ∆/d), где Re – число Рейнольдса для круглоцилиндрических труб; ∆- средняя высота выступов шероховатости стенок трубы, мм; ∆/d - относительная шероховатость стенок трубы, мм.
Можно сделать вывод, что коэффициент гидравлического трения λ зависит от скорости движения жидкости, геометрических размеров поперечного сечения потока, физических свойств жидкости (это следует из формулы 2.1), и от шероховатости стенок труб.
При определении потерь напора необходимо учитывать толщину так называемого вязкого подслоя потока δ (дельта), соотношение толщины которого и выступов шероховатости ∆ определяет трубы как гидравлически гладкие (δ > ∆) или гидравлически шероховатые (δ ≤ ∆).
Толщину вязкого подслоя δ можно определить по формуле:
δ = 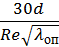 , (2.2)
, (2.2)
| где | λоп - коэффициент гидравлического трения, определяемый опытным путем с использованием формулы (2.1). |
Теоретически коэффициент гидравлического трения λ определяется в зависимости от соотношения толщины вязкого подслоя потока δ и средней высоты выступов шероховатости ∆. Если δ > ∆, то используется формула Блазиуса:
λ =  . (2.3)
. (2.3)
Если δ ≤ ∆, то λ рекомендуется определять по формуле Альтшуля:
λ = 0,11 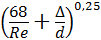 . (2.4)
. (2.4)
Необходимо отметить, что формулы (2.2) … (2.4) справедливы только для турбулентного режима движения жидкости. Поскольку ламинарный режим встречается крайне редко (особенно при движении воды по трубам), то результатом данной лабораторной работы будет определение коэффициента λ как опытным, так и теоретическим путем для турбулентного режима движения жидкости.
При ламинарном режиме λл зависит только от Re и определяется по формуле:
λл =  . (2.5)
. (2.5)
Итак, при изучении потерь напора по длине можно выделить несколько основных этапов:
- необходимо знать и уметь применять уравнение Д. Бернулли с учётом потерь напора:
z1 + 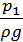 +
+  = z2 +
= z2 + 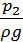 +
+  + hпот, (2.6)
+ hпот, (2.6)
| где | z1 + 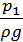 и z2 + и z2 + 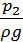 - потенциальная энергия избыточного давления в сечениях 1 – 1 и 2 – 2; - потенциальная энергия избыточного давления в сечениях 1 – 1 и 2 – 2;
 и и  – кинетическая энергия потока жидкости в сечениях 1 – 1 и 2 – 2;
hпот – потери напора на участке между сечениями 1 – 1 и 2 – 2; – кинетическая энергия потока жидкости в сечениях 1 – 1 и 2 – 2;
hпот – потери напора на участке между сечениями 1 – 1 и 2 – 2;
|
-необходимоучесть все факторы, влияющие на величину потерь (скорость течения жидкости, размеры и форму поперечного сечения потока, шероховатость стенок трубы);
- знать и уметь применять формулу Дарси – Вейсбаха (2.1) для определения потерь напора hпот;
- выбрать необходимую формулу для определения коэффициента гидравлического трения λ.
Дата добавления: 2015-04-18; просмотров: 544; Мы поможем в написании вашей работы!; Нарушение авторских прав |