Общие сведения. Гидродинамический напор в рассматриваемом сечении потока при равномерном или плавноизменяющемся течении жидкости согласно уравнению Бернулли (2.6)

Гидродинамический напор в рассматриваемом сечении потока при равномерном или плавноизменяющемся течении жидкости согласно уравнению Бернулли (2.6) определяется по формуле:

Н_d = z + + ,

где

Нd – полный (гидродинамический) напор в выбранном сечении; z – геометрическая высота от плоскости сравнения до центра тяжести сечения (удельная энергия положения); = hр - пъезометрическая высота, представляющая собой высоту столба жидкости в пъезометре (удельная потенциальная энергия, обусловленная давлением); = hV - скоростной напор.

Иными словами, полный (гидродинамический напор) Н_d в рассматриваемом сечении потока равен сумме геометрической высоты z, пъезометрической высоты h_р и скоростного напора h_V:

Н_d = z + h_р + h_V. (4.1)

Линия, проведённая через точки, полученные путём откладывания вверх от плоскости сравнения суммы величин (z + h_р) в различных сечениях потока, называется пъезометрической линией.

Сумма величин (z + h_р) представляет собой пъезометрический напор в выбранном сечении (полная удельная потенциальная энергия жидкости):

Н_р = z + h_р. (4.2)

Линия, проведённая через точки, полученные при откладывании вверх от плоскости сравнения величин Н_d в различных сечениях потока, называется напорной линией.

Напорная линия наглядно демонстрирует изменение гидродинамического напора Н_d (полной удельной энергии) жидкости по длине потока. Уменьшение Н_d вдоль потока, отнесённое к единице его длины, называется гидравлическим уклоном J_e:

J_e = 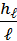, (4.3)

где h_ℓ - потери напора Н_d по длине ℓ потока.

Коэффициент сопротивления системы. Если трубопровод длиной ℓ имеет на всём протяжении несколько k участков с различными диаметрами и на каждом из участков имеются n местных сопротивлений, то общие потери напора системы будут равны:

h_сист= 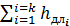+ 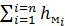, (4.4)

где	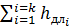-сумма потерь напора по общей длине ℓ потока, состоящей из нескольких k участков с различными диаметрами; -суммапотерь напора в местных сопротивлениях, находящихся на различных k участках.

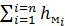Сумма потерь напора по общей длине ℓ потока (потери напора по длине) будет равна:

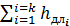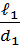
=λ₁ + λ₂ 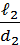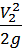+ … + λ_k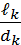 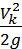, (4.5)

или, учитывая, что λ = ζ_дл , получим

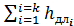=ζ_{дл 1} + ζ_{дл 2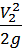} + … + ζ_{дл k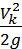} . (4.6)

Сумма потерь напора в местных сопротивлениях по всей длине потока ℓ будет равна:

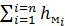= ∑ζ_{м 1} + ∑ζ_{м 2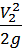} + … + ∑ζ_{м n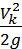} . (4.7)

Подставив полученные выражения (4.6) и (4.7) в выражение для определения общих потерь напора (4.4), получим:

h_сист=(ζ_{дл 1}+ ∑ζ_{м 1}) + (ζ_{дл 2}+ ∑ζ_{м 2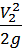}) + … + (ζ_{дл k}+ ∑ζ_{м n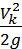}) . (4.8)

Для удобства расчёта потерь напора всей системы h_сист все скорости на разных участках трубопровода (согласно уравнению неразрывности потока) выражают через одну скорость на любом участке трубопровода, обычно на последнем, k – м (V_k):

V₁ = V_k , V₂ = V_k 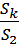и т. д.

Тогда выражение (4.8) примет вид:

h_сист=(ζ_{дл 1}+ ∑ζ_{м 1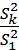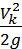}) · · + (ζ_{дл 2}+ ∑ζ_{м 2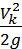}) · + … + (ζ_{дл k}+ ∑ζ_{м n}) · ,

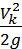или

h_сист=ζ_сист 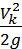, (4.9)

где

ζ_сист = [(ζ_{дл 1}+ ∑ζ_{м 1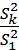}) · + (ζ_{дл 2}+ ∑ζ_{м 2}) + … + (ζ_{дл k}+ ∑ζ_{м n})]. (4.10)

Коэффициент сопротивления системыζ_сист – это сумма коэффициентов потерь напора по длине на различных участках трубопровода с разными площадями живых сечений, и сумма коэффициентов потерь напора в местных сопротивлениях по всей длине трубопровода, отнесённых к одному скоростному напору. Коэффициент сопротивления системы характеризует общие потери напора в неразветвлённом трубопроводе.