Статистический анализ качества изделий в машиностроении. Сущность его на примере точности размера заготовки.

Вопрос № 1.

Статистические анализы качества изделий в машиностроении, которые можно разделить на три категории :

– методы высокого уровня сложности, которые используются разработчиками систем управления предприятиями или процессами. К ним относятся методы кластерного анализа, адаптивные робастные статистики и др.;

– методы специальные, которые применяются при разработке операций контроля, планирования промышленных экспериментов, при расчетах на надежность и т.д.;

– методы общего назначения, которыми должны владеть все работники предприятия, имеющие отношение к качеству и называемые «семь простых методов анализа».

Основное внимание в этой теме уделено «простым методам», как наиболее часто применяемым на практике и рекомендуемым стандартами по качеству: контрольные листки; диаграммы Парето; диаграммы причин и результатов; гистограммы; диаграммы рассеивания; контрольные карты и диаграммы (блок-схемы) потока процессов.

Эффективным инструментом для сбора и автоматического упорядочения данных является контрольный листок – бумажный бланк, на котором заранее напечатаны контролируемые параметры, с тем, чтобы можно было легко и точно записать данные измерений. Его применение позволяет облегчить процесс сбора данных и дальнейшего использования собранной информации. Существует большое количество типов контрольных листков в зависимости от назначения сбора информации: контрольный листок для регистрации видов дефектов, контрольный листке причин дефектов, контрольный листок локализации дефектов, контрольный листок для регистрации распределения измеряемого параметра и др.

Одним из наиболее распространенных на практике методов выявления наиболее значимых (по затратам) дефектов является анализ Парето [2]. Сущность анализа Парето заключается в выявлении таких дефектов, на поиске причин которых необходимо сосредоточить особое внимание. При этом действует правило Парето, что 80% всех дефектов вызвано небольшим числом причин.

Очевидно также, что для производственников важно прояснить картину распределения дефектов и потерь, вызванных отбраковкой продукции, где эти дефекты проявятся. При этом важно устранить причины наиболее многочисленных дефектов. Но в отдельных ситуациях еще важнее выявить причины появления пусть немногочисленных, но приводящих к большим производственным издержкам дефектов. Для этого применяется диаграмма Парето (рис. 1).

Кумулятивная кривая, приведенная на графике, носит название кривой Парето. Из диаграммы видно, что накопленные 80 % соответствуют трем видам дефектов: деформации (Г), царапины (Б) и трещины (А). Именно причины этих дефектов в первую очередь необходимо определить и устранить.

Причинно-следственная диаграмма (диаграмма Исикавы)позволяет выявить и систематизировать взаимосвязь между показателями качества и воздействующими на них факторами (точность и жесткость технологического оборудования, физико-механические свойства материала обрабатываемой заготовки, квалификация рабочего и др.). Японский ученый Каору Исикава первым предложил методику поиска причин, вызывающих вариацию показателей качества, которая получила название «диаграммы Исикавы» (см. рис. 2). Эта диаграмма имеет еще несколько названий: диаграмма причин и результатов, диаграмма «речных притоков», диаграмма «рыбий скелет». Последние два названия связаны с графической интерпретацией диаграммы.

При анализе и регулировании ТП часто возникает необходимость выявления зависимости между отдельными показателями процесса. Например, при обработке резанием важно знать зависимость шероховатости обработанной поверхности от величины подачи или оценить зависимость погрешности формы обрабатываемой поверхности от жесткости технологической системы. Для изучения зависимости между двумя переменными на практике применяют так называемые диаграммы рассеивания (рис. 3).

Диаграмму рассеивания строят для двух статистически связанных между собой переменных. В этом случае ряду изменяющихся значений х соответствует ряд изменяющихся значений у. Такого рода статистическая зависимость между переменными называется корреляционной. Виды корреляционных зависимостей между переменными могут быть линейными и нелинейными, положительными или отрицательными. Возможны ситуации, когда между переменны ми невозможно установить какую-либо зависимость. Наглядная оценка диаграммы рассеивания носит предварительный характер. Для более точной оценки зависимости между переменными проводится математическая обработка массива парных данных, т. е. корреляционный анализ, по результатам которого определяется значение коэффициента корреляции r. Следует отметить, что коэффициент корреляции принимает значения в диапазоне – 1 < r < 1. Можно уверенно считать, что корреляция существует при коэффициенте корреляции r больше |0,6|.

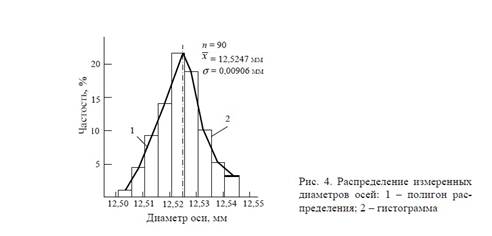
В результате возникновения случайных погрешностей при обработке партии заготовок на настроенных станках действительный размер каждой заготовки является случайной величиной и может принимать любые значения в границах определенного интервала. Совокупность значений действительных значений размеров заготовок, обработанных при неизменных условиях и расположенных в возрастающем порядке с указанием частоты повторения этих размеров или частостей, называется распределением размеров заготовок в партии.

Под частостью понимают отношение числа заготовок одного размера к общему числу заготовок в партии. Распределение действительных размеров заготовок можно представить графически в виде гистограммы распределения, которая представляет собой ступенчатую линию (рис. 4). Для построения гистограммы измеренные действительные значения заготовок разбивают на интервалы таким образом, чтобы цена интервала (разность между наибольшим и наименьшим размерами в пределах одного интервала) была несколько больше цены деления измерительного устройства. Этим компенсируется погрешность измерения.

Частость в этом случае представляет собой отношение числа m заготовок, действительные размеры которых попали в данный интервал, к общему числу заготовок в выборке n. При построении гистограммы по оси абсцисс откладывают интервалы размеров, а по оси ординат соответствующие им частоты m или частости m/n. Затем в каждом интервале строят прямоугольники, высота которых соответствует частоте или частости попадания размеров заготовок в интервал. Построенная таким образом столбчатая диаграмма и есть гистограмма. Последовательным соединением между собой точек, соответствующих серединам интервалов по верхним полкам прямоугольников, получают ломаную кривую, которая носит название эмпирической кривой распределения или полигона

распределения.При увеличении количества интервалов и уменьшении их размеров ломаная эмпирическая кривая распределения приближается по форме к плавной кривой, именуемой кривой распределения. Для построения гистограммы рекомендуется измеренные действительные размеры заготовок разбивать не менее чем на шесть интервалов при общем числе измеренных заготовок не меньше 50.

Анализ построенной гистограммы позволяет сравнить поле рассевания контролируемого параметра ω с полем допуска Т и оценить их взаимное положение. При этом возможны пять типичных вариантов взаимного расположения полей допуска Т и рассеивания w [2]:

- поле рассеивания значительно меньше поле допуска (w < Т). ТП протекает нормально, требуется только поддерживать существующее состояние;

- поле рассеивания равно или немного меньше поля допуска (w = Т). ТП протекает нормально, но нет запаса надежности. Можно провести мероприятия по уменьшению поля рассеивания, если затраты на эти мероприятия будут меньше, чем потери от возможного брака;

- поле рассеивания меньше поля допуска, но смещено влево (или вправо) от границы поля допуска. Процесс протекает ненормально, связан с воздействием специальных причин вариаций, нужно добиться смещения середины поля рассеивания w к центру поля допуска Т;

- поле рассеивания больше поля допуска (w > Т) и размещено симметрично относительно центра поля допуска. Процесс протекает ненормально, связан с воздействием общих причин вариаций, необходимо провести мероприятия по снижению поля рассеивания w;

- поле рассеивания больше поля допуска (w > Т) и смещено относительно середины поля допуска Т. Процесс протекает ненормально, необходимо ликвидировать воздействие как общих, так и специальных причин вариаций.

По результатам такого сравнения можно сделать предварительное заключение об устойчивости ТП и в случае необходимости наметить мероприятия по ее повышению. Более точную оценку устойчивости ТП можно выполнить, используя индексы возможности процесса с учетом Срк и без учета Ср настроенности процесса на середину поля допуска:

Ср = (USL – LSL) / 6s;

Срк = min {[(USL – ) / 3s]; [( – LSL) / 3s]},

где USL, LSL – соответственно наибольшее и наименьшее значения контролируемого параметра заготовки, мм; s – оценка среднего квадратического отклонения, мм; – среднее арифметическое значение контролируемого параметра, мм.