
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нумерація чисел в межах 10 4 страница
Наступний урок відводиться для розвитку вмінь виконувати додавання двоцифрових чисел без переходу через десяток. На цьому уроці можна запровадити коротке пояснення (без з'ясування розкладу на розрядні доданки). Подаємо зразок такого пояснення: 63 + 25; до числа 60 додати 20, буде 80; до числа 3 додати 5, буде 8; до числа 80 додати 8, буде 88; отже, 63 + 25 = 88. Щоб коментування відбувалося швидко, можна замість слова "додати" вживати слово "плюс" або сполучник "і".
Окремі випадки додавання (54 + ЗО; 54 + 3; 20 + 47; 2 + 47). До окремих випадків додавання належать такі суми, в яких в одному з доданків відсутні одиниці або десятки. За своєю сутністю тема продовжує формувати вміння застосовувати загальне правило додавання двоцифрових чисел. Наведемо зразки пояснень виконання обчислень.
54 + 30. У другому доданку немає одиниць. Отже, треба додати 50 і 30 і до знайденого результату додати 4: 50 + 30 = 80, 80 + 4 = 84.
54 + 3. У другому доданку: немає десятків. Отже, треба додати 4 і З, а результат додати до 50: 4 + 3 = 7; 50 + 7 = 57.
2 + 47. У першому доданку немає десятків. Отже, треба додати 2 і 7, а результат додати до 40: 2 + 7 = 9; 40 + 9 = 49.
При короткому поясненні не вказують, які розрядні одиниці відсутні, а відразу виконують дії. Наприклад, обчислення виразу 20 + 47 коментується так: 20 плюс 40 — шістдесят; 60 плюс 7 — шістдесят сім.
Застосування загального прийому до окремих випадків проводять на основі опорних записів, але у разі виникнення труднощів варто застосовувати предметне ілюстрування (бруски-десятки і окремі кубики, смужки з кружечками).
Методика викладання математики в початкових класах
На одному з уроків закріплення варто ознайомити учнів з прийомом послідовного додавання двоцифрового числа. На основі опорних записів їм пропонують пояснити і порівняти послідовність виконання таких обчислень:
26 + 63=[] 26 +- 63 = □
-т 26+ 60 = 86' ■іНЬ86 + 3 = 89 :1
20 + 60 = 80
6+3 = 9
80 + 9 = 89
Віднімання двоцифрових чисел без переходу через десяток. Теоретичною основою порозрядного віднімання двоцифрових чисел є правило віднімання суми від суми. У 2 класі це правило не вивчають. Пояснення подають за аналогією до прийому порозрядного додавання. Так, наприклад, прийом обчислення ілюструється предметними діями та відповідними записами. їх зміст відображено на мал. 89. 58 - 34 = []
50 - ЗО = 20; 8-4 = 4; 20 + 4 = 24
Десятки • Одиниці

Мал. 89
Після виконання двох операцій учитель ставить запитання:
Скільки десятків залишилось? Скільки одиниць залишилось? Яке число отримали?
Учням пропонують розглянути записи і пояснити обчислення. Потім формулюють правило: віднімаючи двоцифрові числа, десятки віднімаються від десятків, одиниці — від одиниць.
До окремих випадків віднімання належать такі різниці, в яких від'ємник не містить одиниць або десятків: 79 — 40, 79 — 2. Повідомлення теми можна зробити на основі таких вправ:
1. Від смужки завдовжки 36 см відрізали 2 см. Скільки сантиметрів становить довжина смужки? 2. Від смужки завдовжки 36 см відрізали 2 дм. Скільки сантиметрів становить довжина смужки?
Спочатку при поясненні вказуємо на особливість від'ємника.
79 — 40. У від'ємнику одиниць немає, треба відняти тільки десятки. 70 мінус 40 — тридцять; ЗО плюс 9 — тридцять дев'ять.
79 — 2. У від'ємнику немає десятків, треба відняти тільки одиниці. 9 мінус 2 — сім; 70 плюс 7 — сімдесят сім.
Згодом обчислення коментуємо без вказівки на особливість від'ємника.
На одному з останніх уроків закріплення варто ознайомити учнів з прийомом послідовного віднімання.
Розділ VII. Нумерація чисел 21—100. Арифметичні дії в межах 100
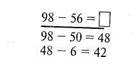
Методика викладання математики в початкових класах
Письмове додавання і віднімання двоцифрових чисел. Основна відмінність у виконанні письмового й усного додавання і віднімання полягає в тому, що усні обчислення починають з вищих розрядів, а письмові — з нижчих.
Для ознайомлення дітей з письмовим додаванням і відніманням застосовують метод пояснення. Можна використати нумераційну таблицю, в якій записані числа 28 і 45 (табл. 19).
Таблиця 19
| Десятки | Одиниці |
Учитель пропонує учню додати ці числа і записати результати додавання у нумераційну таблицю. Учень додає спочатку десятки, а потім одиниці, отримує 6 дес. і 13 од., записує це у нумераційну таблицю. Перевіривши записи, вчитель повідомляє, що десятки і одиниці додано правильно, але запис відповіді треба уточнити. 13 од. — це 1 дес. і 3 од. Треба 1 дес. зарахувати до десятків. Отже, відповідь буде така: 7 дес. і 3 од. Без нумераційної таблиці цей приклад можна записати так: + 28 45_
Числа тут записано у стовпчик: одиниці під одиницями, десятки під десятками. Щоб відповідь не записувати двічі, додають спочатку одиниці, а потім десятки: 8 додати 5, буде 13. 13 — це 1 дес. і 3 од.; З од. пишемо під одиницями, а десятки додамо до десятків. 2 дес. плюс 4 дес, буде 6 дес. і ще 1 дес, буде 7 дес. Цифру 7 запишемо під десятками.
Додавання "стовпчиком" називають письмовим додаванням.
У ході закріплення учні виконують такі завдання:
1) Перевірте, чи правильно додали числа, записані в нумераційній таблиці, і поясніть, чому відповідь було записано двічі.
2) Прочитайте за підручником пояснення про письмове додавання.
3) Знайдіть суму двох двоцифрових чисел і поясніть обчислення. Учитель звертає увагу учнів на те, що при письмовому додаванні також
додають десятки до десятків і одиниці до одиниць, але починають додавання з одиниць.
На наступних уроках вводять коротку форму пояснення письмового додавання.
Знайти суму 47 + 29. Зразок короткого пояснення: 7 + 9 — шістнадцять, 6 пишу, 1 запам'ятовую; 4 і 2 — шість та ще 1 — сім, пишу 7, всього 76.;
+ 47
л
~76
Якщо вчитель не ставить вимогу дати повне пояснення, то учні користуються короткою формою пояснення.
Розглянемо пояснення письмового віднімання двоцифрових чисел з переходом через десяток.
Піднімання чисел можна також виконувати письмово. Від'ємник записують під зменшуваним так, щоб одиниці були під одиницями, а десятки під десятками. При письмовому обчисленні спочатку віднімають одиниці, (найдемо письмово різницю чисел 82 і 35. Запишемо числа стовпчиком. .■■-. мхї _82
■■•'■'Жо 35 '■■'
~47
Пояснення. Від 2 од. не можна відняти 5 од. Беремо 1 дес. з 8 дес; 1 дес. І 2 од. — це 12. Від числа 12 відняти 5, буде 7. Запишемо цифру 7 на місце одиниць.
Від 7 дес. відняти 3 дес, буде 4 дес. Запишемо цифру 4 на місці десятків. Отримали число 47.
На наступному уроці учням подається зразок короткого пояснення письмового віднімання 86. _86
16 мінус 7, буде дев'ять, пишемо 9. 7 мінус 5, буде два, пишемо 2; всього 29.
Усне додавання з переходом через десяток. Усне додавання двоцифрових чисел з переходом через десяток виконуємо порозрядним додаванням. І Іаприклад, обчислюючи вираз 28 + 59, міркуємо так: 20 плюс 50, буде 70; 8 плюс 9, буде 17; 70 плюс 17, буде 87. З поданого зразка видно, що такий спосіб обчислення охоплює додавання круглих десятків, табличне додавання і переходом через десяток і додавання двоцифрового числа до круглого. З урахуванням цього і будують уроки на ознайомлення з новим матеріалом.
Додавання двоцифрових чисел з переходом через розряд розглядають у гакій послідовності: загальний випадок (наприклад, 28 + 59), окремі випадки ' пиду 38 + 4, 7 + 25, 42 + 8, 4 + 36, 36 + 54.
Розглянемо загальний випадок додавання виду 26 + 47.
Підготовчі вправи: а) обчисліть вирази і поясніть їх обчислення: 30 + 40; N І- 6; 80 + 19; б) обчисліть вирази, користуючись переставною властивістю дії додавання: 20 + 4 + 60 + 5; 30 + 8 + 20 + 9.
Розділ VII. Нумерація чисел 21—100. Арифметичні дії в межах 100
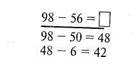
Методика викладання математики в початкових класах
Письмове додавання і віднімання двоцифрових чисел. Основна відмінність у виконанні письмового й усного додавання і віднімання полягає в тому, що усні обчислення починають з вищих розрядів, а письмові — з нижчих.
Для ознайомлення дітей з письмовим додаванням і відніманням застосовують метод пояснення. Можна використати нумераційну таблицю, в якій записані числа 28 і 45 (табл. 19).
Таблиця 19
| Десятки | Одиниці |
Учитель пропонує учню додати ці числа і записати результати додавання у нумераційну таблицю. Учень додає спочатку десятки, а потім одиниці, отримує 6 дес. і 13 од., записує це у нумераційну таблицю. Перевіривши записи, вчитель повідомляє, що десятки і одиниці додано правильно, але запис відповіді треба уточнити. 13 од. — це 1 дес. і 3 од. Треба 1 дес. зарахувати до десятків. Отже, відповідь буде така: 7 дес. і 3 од. Без нумераційної таблиці цей приклад можна записати так: + 28 45_
Числа тут записано у стовпчик: одиниці під одиницями, десятки під десятками. Щоб відповідь не записувати двічі, додають спочатку одиниці, а потім десятки: 8 додати 5, буде 13. 13 — це 1 дес. і 3 од.; З од. пишемо під одиницями, а десятки додамо до десятків. 2 дес. плюс 4 дес, буде 6 дес. і ще 1 дес, буде 7 дес. Цифру 7 запишемо під десятками.
Додавання "стовпчиком" називають письмовим додаванням.
У ході закріплення учні виконують такі завдання:
1) Перевірте, чи правильно додали числа, записані в нумераційній таблиці, і поясніть, чому відповідь було записано двічі.
2) Прочитайте за підручником пояснення про письмове додавання.
3) Знайдіть суму двох двоцифрових чисел і поясніть обчислення. Учитель звертає увагу учнів на те, що при письмовому додаванні також
додають десятки до десятків і одиниці до одиниць, але починають додавання з одиниць.
На наступних уроках вводять коротку форму пояснення письмового додавання.
Знайти суму 47 + 29. Зразок короткого пояснення: 7 + 9 — шістнадцять, 6 пишу, 1 запам'ятовую; 4 і 2 — шість та  ще 1 — сім, пишу 7, всього 76%
ще 1 — сім, пишу 7, всього 76%
Якщо вчитель не ставить вимогу дати повне пояснення, то учні користуються короткою формою пояснення.
Розглянемо пояснення письмового віднімання двоцифрових чисел з переходом через десяток.
Піднімання чисел можна також виконувати письмово. Від'ємник записують під зменшуваним так, щоб одиниці були під одиницями, а десятки під десятками. При письмовому обчисленні спочатку віднімають одиниці, (найдемо письмово різницю чисел 82 і 35. Запишемо числа стовпчиком. .■■-. мхї _82
■■•'■'Жо 35 '■■'
~47
Пояснення. Від 2 од. не можна відняти 5 од. Беремо 1 дес. з 8 дес; 1 дес. І 2 од. — це 12. Від числа 12 відняти 5, буде 7. Запишемо цифру 7 на місце одиниць.
Від 7 дес. відняти 3 дес, буде 4 дес. Запишемо цифру 4 на місці десятків. Отримали число 47.
На наступному уроці учням подається зразок короткого пояснення письмового віднімання 86. _86
16 мінус 7, буде дев'ять, пишемо 9. 7 мінус 5, буде два, пишемо 2; всього 29.
Усне додавання з переходом через десяток. Усне додавання двоцифрових чисел з переходом через десяток виконуємо порозрядним додаванням. І Іаприклад, обчислюючи вираз 28 + 59, міркуємо так: 20 плюс 50, буде 70; 8 плюс 9, буде 17; 70 плюс 17, буде 87. З поданого зразка видно, що такий спосіб обчислення охоплює додавання круглих десятків, табличне додавання і переходом через десяток і додавання двоцифрового числа до круглого. З урахуванням цього і будують уроки на ознайомлення з новим матеріалом.
Додавання двоцифрових чисел з переходом через розряд розглядають у кікій послідовності: загальний випадок (наприклад, 28 + 59), окремі випадки ' пиду 38 + 4, 7 + 25, 42 + 8, 4 + 36, 36 + 54.
Розглянемо загальний випадок додавання виду 26 + 47.
Підготовчі вправи: а) обчисліть вирази і поясніть їх обчислення: 30 + 40; N І- 6; 80 + 19; б) обчисліть вирази, користуючись переставною властивістю дії додавання: 20 + 4 + 60 + 5; 30 + 8 + 20 + 9. 154
Розділ VII. Нумерація чисел 21-100. Арифметичні дії в межах 100
Методика викладання математики в початкових класах
Пояснення нового матеріалу. Додавання двоцифрових чисел з переходом через десяток ми навчилися виконувати письмово. Проте такі числа треба вміти додавати усно. Знайдемо усно суму чисел 26 і 47.
26 /\
20 + 6
40 + 7
20 + 40 = 70 6 + 7 = 13 60 + 13 = 73
Запишемо суму в рядок і кожне число розкладемо на десятки й одиниці. Використовуючи переставну властивість, додамо спочатку десятки, а потім одиниці: 20 плюс 40, буде 60; 6 плюс 7, буде 13. Тепер додамо утворені суми: 60 + 13 = 73. Отже, сума чисел 26 і 47 дорівнює 73.
Після розгляду загального випадку учні можуть самостійно вказати способи обчислення окремих випадків додавання двоцифрових чисел з переходом через десяток.
Розглянемо випадок 38 + 4. У другому доданку немає десятків. Додамо число 4 до одиниць першого доданка. 8 + 4 = 12. Результат додамо до десяткін першого доданка: 30 + 12 = 42.
Зразок короткого пояснення: 8 і 4, буде 12; ЗО і 12, буде 42.
Після опрацювання окремих випадків можна ознайомити учнів :і прийомом послідовного додавання.
36 + 58 = П
/\
50 8
36 + 50 = 86 86 + 8 = 94
Усне віднімання з переходом через десяток. Порозрядне усне віднімання двоцифрових чисел з переходом через десяток потребує передбачення, що один десяток зменшуваного буде необхідний для віднімання одиниць від'ємника. Тому краще загальним прийомом вважати спосіб послідовного віднімання.
83-27 = []
83 - 20 = 63 63 - 7 = 56
Він спирається на вміння віднімати одноцифрове число від двоцифрового з переходом через десяток. Обчислення в цьому випадку можна виконати двома способами:
63-7 = П 63 - 7 = [] .■■;■
63 - 3 = 60 60 - 4 = 56
13-7 = 6 50 + 6 = 56
У класі розглядають обидва способи, але перевага надається першому.
Таким чином, загальному прийому віднімання передує ознайомлення учнів з випадками віднімання виду 40 - 8 і 63 - 7.
Віднімання виду 40 - 8 і 63 — 7 можна опрацювати методом пояснення, самостійно за записами та малюнком підручника, за допомогою стрічок з кружечками або за допомогою малюнка і пояснення до нього. Розглянемо спосіб обчислення 40 - 8 за малюнком підручника і за записами в ньому.
Нам треба навчитися віднімати одноцифрові числа від круглих десятків. У підручнику є опис послідовності віднімання, малюнок до нього і саме пояснення. Розгляньте їх і прочитайте пояснення (мал. 90). Розкажіть, як відняли 8 від 40.
40 - 8 = 32 /Ч 30 10
-.х>г.1О — 8 = 2.
щд ЗО + 2 = 32
Мал. 90
Після розгляду цих окремих випадків віднімання можна ознайомити учнів із загальним випадком віднімання двоцифрових чисел з переходом через десяток.
Тема "Віднімання двоцифрових чисел з переходом через десяток (загальний випадок 34 — 16)".
Підготовчі вправи:
63-20-3 45-10-5 91-40-1 63 - 20 - 7 45 - 10 - 9 91 - 40 - 6
Пояснення нового матеріалу. Знаходження різниці 34 - 16 на основі предметних дій з пучками-десятками і окремими паличками.
Утворимо число 34 з пучків-десятків і окремих паличок. Візьмемо 3 пучки-десятки і 4 палички. Нам треба відняти число 16, тобто відняти 1 дес. і 6 од. Піднімемо 1 пучок-десяток від 3 пучків-десятків, залишиться 2 пучки-десятки. ІЦе треба відняти 6 паличок. Віднімемо спочатку 4 палички. Залишиться тільки 2 пучки-десятки. Залишилося від 20 відняти 2; 20 - 2 = 18. Отже, 34 - 16 = 18..
Пояснення розв'язання за підручником' 84 - 29 = []
84-20 = 64 64 - 9 = 55

Розділ VII. Нумерація чисел 21-100. Арифметичні дії в межах 100
На кожний із розглянутих випадків додавання і віднімання та на закріплення в кінці теми присвячують 2—3 уроки. Частину часу уроків відводять для відтворення прийомів обчислень (коментоване розв'язування прикладів), але основним у роботі з формування навичок є застосування обчислювальних прийомів у різних ситуаціях.
Додавання і віднімання двоцифрових чисел з переходом через десяток для учнів важче, ніж без переходу через десяток. Тому не слід поспішати з обчисленням виразів на дві операції. Перші вирази на дві операції треба розв'язувати з коментуванням. Для закріплення необхідно добирати активні форми постановки завдань.
§25. Складання і засвоєння таблиць множення та ділення
Матеріал теми в 2 класі вивчають у такій послідовності: розкриття конкретного змісту дії множення; складання таблиці множення числа 2; розкриття конкретного змісту дії ділення; зв'язок між діями множення і ділення; складання таблиць ділення на 2; складання таблиці множення числа З і ділення на 3 та для чисел 4 і 5.
Ознайомлення з дією множення. Подаємо фрагменти уроку з розкриття конкретного змісту дії множення. Розглядаючи малюнки (мал. 91, 92), учні дають відповіді на запитання: "Скільки всього вишень?" та "Скільки всього жолудів?


Мал. 91
Мал. 92
Учитель записує на дошці:
2 + 2 + 2 + 2 + 2= 10 2 + 2 + 2 + 2 = 8
Після цього запитує, яку рівність слід було би записати, якби виставили 6 пар вишень, 7 пар жолудів.
Діти розглядають першу суму. В цій сумі 5 доданків, кожний з яких дорівнює 2. Вчитель повідомляє, що додавання однакових доданків називається множенням. Суму однакових доданків 2 + 2 + 2 + 2 + 2= 10 записують так: 2 • 5 = 10. У цій рівності перше число (число 2) є тим, що у сумі було доданком, а друге число (число 5) показує, скільки разів перше число (число 2) взято доданком. Крапка між числами — це знак множення. Рівність треба читати так: 2 помножити на 5, дорівнює 10.
Учитель зазначає, що другу суму теж можна записати дією множення. На дошці і в зошитах записи мають вигляд:
2 + 2 + 2 + 2 + 2=10 2 + 2 + 2 + 2 = 8
2 • 5= 10 2-4 = 8
Методика викладання математики в початкових класах
Підсумовуємо, що означають перше і друге числа в цих рівностях на множення. Потім учням пропонується виконати такі завдання:
1. Запишіть який-небудь вираз на додавання одноцифрового числа, а потім іамініть його виразом на множення. Поясніть, що означає кожне число у ниразі на множення.
2. Замініть вираз на множення 3 • 5 виразом на додавання.
3. Складіть і розв'яжіть за малюнком задачу (мал. 93). Розв'язання задачі учні записують за допомогою додавання і множення.

Мал. 93
На наступному уроці учні продовжують вчитися читати вирази на множення, виконують вправи на заміну додавання однакових доданків множенням і множення додаванням. Зміст вправ можна ускладнити: замінити, де можна, вирази на додавання виразами на множення. Наприклад: 4 + 4 + 4 + 4; 14+14+14; 23 + 32.
На цьому самому уроці вводять назви чисел при множенні.
Складання таблиці множення числа 2. Підготовча вправа. Прочитайте рівність 2 • 4 = 8. Що показує другий множник? Як перевірити відповідь?
Пояснення нового матеріалу. Знаходити добуток за допомогою додавання незручно. Треба скласти і вивчити результати множення числа 2 на числа 2, З, 4, 5, 6, 7, 8 і 9, тобто скласти таблицю множення числа 2.
Скільки буде 2 • 2? (4.) Чому? (2 + 2 = 4.) Скільки буде 2 • 3? (6.) Чому? (2 + 2 + 2 = 6.)
Таблиця множення числа 2 наведена в підручнику. Перевіримо кожний результат таблиці самостійно, користуючись наведеними виразами (табл. 20).
Таблиця 20
| 2 - | (-2 | •2 = 4 | |||||
| 2- | 1- 2- | 1- 2 | •3 = 6 | ||||
| 2 - | (- 2 - | Ь 2 - | ї 2 | •4 = 8 | |||
| 2- | Ь2 - | 1-2 - | *- 2- | 1-2 | • 5= 10 | ||
| 2 - | і- 2 - | 1- 2 - | і- 2 - | *■ 2 | + 2 | •6= 12 | |
| 2- | 1- 2- | 1- 2 - | і- 2 - | 1- 2 | + 2 + 2 | •7= 14 | |
| 2- | І-2Н | -2Н | -2 -+ | -24 | -2+2+2 | 8=16 | |
| 2- | Ь 2 Н | -■2-і | -24 | -24 | -2+2+2+2 | ■9= 18 |
158 Розділ VII. Нумерація чисел 21-100. Арифметичні дії в межах 100
Для засвоєння таблиці множення числа 2 використовують такі типи завдань: завдання, що виконують з безпосереднім використанням таблиці множення числа 2; вправи на відтворення таблиці множення числа 2; вправи на використання знань табличних результатів та завдання на складання і розв'язування задач. Подамо зразки^ завдань кожного виду.
Завдання, що виконують за таблицею:
1. Користуючись таблицею, знайдіть значення виразів:
2-5+10; 2-7-7; 2-7-5.
2. Користуючись таблицею, розв'яжіть задачу.
На кожній тарілці дві груші. Скільки груш на 6-ти тарілках? Вправи на відтворення таблиці:
1. Прочитайте таблицю множення числа 2 (із зошита чи дошки). Поясніть, як дізналися, що 2 • 6 = 12.
2. Прочитайте таблицю множення числа 2 за поданим записом:
| 2-2 | 2-3 | 2-4 | 2-5 | 2-6 | 2-7 | 2-8 | 2-9 |
"З. Прочитайте таблицю множення числа 2, користуючись т|щім записом:
4. Скажіть таблицю множення числа 2 напам'ять.
5. Скажіть напам'ять таблицю множення числа 2, починаючи з більшого числа (2 ■ 9, 2 • 8 і т. д.).
6. Вибірково назвіть табличні результати. Скільки буде, якщо 2 помножити на 5? На 9? На 7?
7. Назвіть тільки результати таблиці множення числа 2 (4, 6, 8,..., 18). Вправи на використання табличних результатів:
1. Розгляньте записи і поясніть розв'язання:
2-7= 14 14 + 5= 19
2. Запишіть коротше і знайдіть значення виразів:
2 + 2 + 2 + 2 + 9; 2 + 2 + 2 + 2 + 2-7.
3. Знайдіть значення виразів:
2-9 + 5; 2-7-8; 2-3-6.
4. Порівняйте вирази:
2-9[]12; 2-7[]2 + 7; 2-6[]6 + 6. '
5. Купили 4 книжки по 2 грн. кожна і альбом за 3 грн. Скільки гривень коштує покупка?
6. У брата 4 монети по 2 коп., а у сестри — на 3 коп. більше. Скільки копійок у сестри?
Методика викладання математики в початкових класах
Ознайомлення з дією ділення. Ознайомлення з дією ділення та з'ясування іп'язку між дією множення і ділення будується на предметних ситуаціях. Ьс:іиосередньо практична робота учнів обмежується поділом смужок на 2 або 4 ріпні частини.
Розглянемо практичну задачу. Візьмемо 6 груш. Розкладемо їх на 3 тарілки корінну в кожну (мал. 94). Скільки груш на кожній з цих тарілок?

Мол. 94
Це задача на ділення. Розв'язання її записують так:
6:3 = 2(гр.)
Відповідь. 2 груші. ■
Дві крапки (:) — знак ділення. Ділення — це четверта арифметична дія.;:
Рівності на ділення читають так: шість поділити на три, буде два.
Для первинного закріплення учням пропонують такі завдання:
1. Прочитайте рівності.
10 : 2 = 5; 6 : 3 == 2; 100 : 10= 10.
2. Смужку завдовжки 12 см поділіть на дві рівні частини (перегинанням); Ча виконаною роботою складіть і запишіть вираз на ділення. Обчисліть його. Прочитайте рівність.
Зв'язок між діями множення і ділення. У рівностях 2 • 6=12і12:2 = 6 однакові числа. Можна сказати, що рівність на ділення складено з рівності па множення. Розглянемо смужку, до якої пришиті ґудзики (мал. 95).

Мал. 95
До смужки пришито 5 стовпчиків ґудзиків по 2 ґудзики у кожному, їх кількість можна обчислити додаванням: 2 + 2 + 2 + 2 + 2= 10 (г.) або множенням: 2 • 5 = 10 (ґ.).
Розріжемо смужку вздовж на 2 частини, щоб у кожній було ґудзиків порівну (мал. 96). Бачимо, що в кожній частині 5 ґудзиків. Отже, можна скласти таку рівність на ділення: 10:2 = 5 (г.)
Візьмемо ще одну таку саму смужку з десятьма ґудзиками і розріжемо її на 5 частин, щоб у кожній була однакова кількість ґудзиків (мал. 97). Отримали в кожній частині по 2 ґудзики. У цьому випадку матимемо таку рівність наділення: 10 : 5 = 2 (г.) ,а. " .ю»я,; \160
Розділ VII. Нумерація чисел 21-100. Арифметичні дії в межах 100

Мал. 97
Учитель підсумовує, що з рівності 2 • 5= 10 отримали дві рівності наділення: 10:2 = 5і 10:5 = 2. У першій рівності добуток ділили на перший множник — на 2, а в другому — на другий множник — на 5. Отже, якщо множники різні, то з кожної рівності на множення можна скласти дві рівності на ділення.
Складання таблиці ділення на 2. Багато практичних завдань, математичних задач потребують застосування дії ділення. Ділення одного числа на інші' виконують за певним правилом, але спочатку треба вивчити таблиці ділення. Таблиці ділення складають за таблицями множення, а потім їх завчають напам'ять.
За прикладом 2-6=12 можна скласти такий приклад наділення: 12:2 = 6. Саме так складають всю таблицю ділення на 2. Запишемо в стовпчик зліва множення числа 2, а справа від нього — таблицю ділення на 2. :2 = 2 2 = З 2 = 4 2 = 5 2 = 6 2 = 7 2 = 8 2 = 9
Далі вчитель пропонує прочитати й записати таблицю ділення на 2 у зошит, обчислити з використанням таблиці кілька виразів та розв'язати 1-2 задачі. Для засвоєння таблиці ділення на 2 використовують різні завдання на її відтворення та застосування табличних результатів у ході обчислень та розв'язування задач. За формою подання вони подібні до завдань на засвоєння таблиці множення числа 2. Як класу, так і одному учню варто частіше ставити парне завдання: прочитати таблицю множення числа 2, а потім — таблицю ділення на 2.
Засвоєння таблиць ділення є тривалим процесом, тому варто дозволяти дітям користуватися готовими таблицями протягом всього часу вивчення їх у 2 класі.
| 2-2 = 4 | 4: |
| 2-3 = 6 | 6 : |
| 2-4 = 8 | 8 : |
| 2 • 5 = 10 | |
| 2-6= 12 | |
| 2 • 7 = 14 | |
| 2-8= 16 | |
| 2-9= 18 |
Методика викладання математики в початкових класах
Порівняння простих задач на ділення. За змістом задачі на ділення поділяються на два види: ділення на рівні частини і ділення на вміщення. З першим видом задач учні ознайомлюються вже в процесі вивчення дії ділення, п з другим — на другому уроці після складання таблиці ділення на 2.
Задачі з ділення на вміщення вводяться у порівнянні з задачею на ділення па рівні частини. Цим самим ставиться мета відразу узагальнити процес розв'язування задач наділення. Характер задачі визначається лише за назвою результату ділення. Сам вираз на ділення читається в обох випадках однаково, наприклад, 12 поділити на 3.
Бесіду на порівняння задач і узагальнення процесу розв'язування задач можна провести за матеріалами завдання підручника, в якому пропонується порівняти розв'язання і відповіді задач (поділ 12 морквин на 3 рівні частини і поділ 12 морквин на пучки, по 3 морквини в пучку). Учні порівнюють розв'язання цих задач і встановлюють, що для розв'язання обох задач було складено однаковий вираз: 12 : 3, тому й числові відповіді однакові — 4. Найменування відповідей різні. Отже, при розв'язуванні задач наділення треба уважно подумати, якою буде назва результату.
Дата добавления: 2015-04-18; просмотров: 299; Мы поможем в написании вашей работы!; Нарушение авторских прав |