В экономике предприятия

ДИФФЕРЕНЦИАЛ– линейная часть приращенияфункции. Пусть функция y = f(x) дифференцируема на отрезке [a,b]. Производная этой функции в некоторой точке x отрезка [a,b] определяется равенством

.

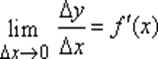Отношение 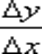стремится к определенному числу f ў(x)и, следовательно, отличается от производной f ў(x)на величину бесконечно малую:

,

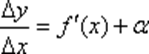где a ® 0 при Dx ® 0.

Умножение всех членов последнего равенства на Dx дает

Dy = fў(x)Dx + aDx.

Так как 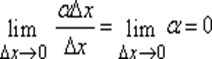, то приращение Dy функции состоит из двух слагаемых, из которых первое слагаемое есть (при f ў(x) № 0) так называемая главная часть приращения, линейная относительноDx.Произведение f ў(x)Dx называют дифференциалом функции и обозначают через dy или df(x):

dy = f ў(x)Dx

Можно найти дифференциал функции y = x. В этом случае yў = (x)ў = 1и, следовательно,

Dy = dx =Dx. Таким образом, дифференциал dx независимой переменной x совпадает с ее приращением Dx.

Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.

Процесс нахождения интеграла называется интегрированием.

Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения.

Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является интеграл Римана.

Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x Î X справедливо равенство:

F¢ (x) = f(x). (8.1)

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -

ò f(x) dx.

Если F(x) - какая-нибудь первобразная для функции f(x), то

ò f(x)dx = F(x) + C, (8.2)

где С - произвольная постоянная.

Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:

1) d ò f(x)=f(x)dx,

2) ò df(x)=f(x)+C,

3) ò af(x)dx=aò f(x)dx (a=const),

4) ò(f(x)+g(x))dx= ò f(x)dx+ ò g(x)dx.