Тесты 2-го блока сложности

1. Значения точек и , вычисленные по методу золотого сечения на первой итерации, при поиске минимума функции, на отрезке неопределенности [5,5.5] равны…

1) x₁ = 5.309, x₂ = 5.191; *

2) x₁ = 5.260, x₂ = 5.240;

3) x₁ = 5.447, x₂ = 5.353;

4) x₁ = 5.147, x₂ = 5.053.

2. Значения точек и , вычисленные по методу дихотомии на первой итерации, с при поиске минимума функции, на отрезке неопределенности [-1,0] ( ) равны…

1) x₁ = -0.49, x₂ = -0.51; *

2) x₁ = -0.48, x₂ = -0.52;

3) x₁ = -0.38, x₂ = -0.62;

4) x₁ = 0.49, x₂ = 0.51;.

3. Значения точек и , вычисленные по методу золотого сечения на первой итерации, при поиске минимума функции, на отрезке неопределенности [10,12] равны…

1) x₁ = 11.236, x₂ = 10.764; *

2) x₁ = 11.364, x₂ = 10.636;

3) x₁ = 11.011, x₂ = 10.099;

4) x₁ = 11.005, x₂ = 10.995.

4. Значения точек и , вычисленные по методу дихотомии на первой итерации, при поиске минимума функции, на отрезке неопределенности [-2,-1.5] ( ) равны…

1) x₁ = -1.74, x₂ = -1.76; *

2) x₁ = -1.69, x₂ = -1.81;

3) x₁ = -1.73, x₂ = -1.77;

4) x₁ = -1.59, x₂ = -1.61.

5. Значения точек и , вычисленные по методу золотого сечения на первой итерации, при поиске минимума функции, на отрезке неопределенности [1.5,2] равны…

1) x₁ = 1.809, x₂ = 1.691; *

2) x₁ = 1.841, x₂ = 1.659;

3) x₁ = 1.761, x₂ = 1.749;

4) x₁ = 1.755, x₂ = 1.745.

6. Значения точек и , вычисленные по методу дихотомии на первой итерации, при поиске минимума функции, на отрезке неопределенности [-1,1] ( ) равны…

1) x₁ = 0.01, x₂ = -0.01; *

2) x₁ = 0.24, x₂ = -0.24;

3) x₁ = 0.36, x₂ = -0.36;

4) x₁ = 0.02, x₂ = -0.02.

7. Значения точек и , вычисленные по методу золотого сечения на первой итерации, при поиске минимума функции, на отрезке неопределенности [0.5,0.8] равны…

1) x₁ = 0.685, x₂ = 0.615; *

2) x₁ = 0.705, x₂ = 0.595;

3) x₁ = 0.655, x₂ = 0.645;

4) x₁ = 0.747, x₂ = 0.653.

8. Значения точек и , вычисленные по методу дихотомии на первой итерации, при поиске минимума функции, на отрезке неопределенности [1,1.5] ( ) равны…

1) x₁ = 1.26, x₂ = 1.24; *

2) x₁ = 1.31, x₂ = 1.19;

3) x₁ = 1.34, x₂ = 1.16;

4) x₁ = 1.27, x₂ = 1.23.

9. Значения точек и , вычисленные по методу золотого сечения на первой итерации, при поиске минимума функции, на отрезке неопределенности [0,0.8] равны…

1) x₁ = 0.494, x₂ = 0.306; *

2) x₁ = 0.546, x₂ = 0.254;

3) x₁ = 0.414, x₂ = 0.391;

4) x₁ = 0.405, x₂ = 0.395.

10. Значения точек и , вычисленные по методу дихотомии на первой итерации, с целью нахождения точки минимума функции, на отрезке неопределенности [1.6,2] ( ) равны…

1) x₁ = 1.81, x₂ = 1.79; *

2) x₁ = 1.85, x₂ = 1.75;

3) x₁ = 1.87, x₂ = 1.73;

4) x₁ = 1.82, x₂ = 1.78.

11. Длина отрезка неопределенности после 10-ти итераций по методу дихотомии ( 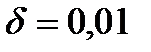), если минимум отделен на отрезке [4,5], равна…

1) 0.021; *

2) 0.011;

3) 0.192;

4) 0.356.

12. Длина отрезка неопределенности после 5-ти итераций по методу дихотомии ( ), если минимум отделен на отрезке [3,5], равна…

1) 0.064; *

2) 0.28;

3) 0.812;

4) 0.127.

13. Длина отрезка неопределенности после 10-ти итераций по методу золотого сечения, если минимум отделен на отрезке [3,5], равна…

1) 0.016; *

2) 0.222;

3) 0.124

4) 0.026.

14. Длина отрезка неопределенности после 6-ти итераций по методу золотого сечения, если минимум отделен на отрезке [2,4], равна…

1) 0.111; *

2) 0.051;

3) 0.201;

4) 0.099.

15. Длина отрезка неопределенности после 5-ти итераций по методу дихотомии ( 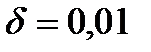), если минимум отделен на отрезке [2,5], равна…

1) 0.113; *

2) 0.103;

3) 0.270;

4) 0.098.

16. Длина отрезка неопределенности после 3-х итераций по методу дихотомии ( 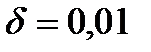), если минимум отделен на отрезке [0.1,0.6], равна…

1) 0.08; *

2) 0.23;

3) 0.33;

4) 0.56.

17. Длина отрезка неопределенности после 4-х итераций по методу золотого сечения, если минимум отделен на отрезке [0.5,0.6], равна…

1) 0.015; *

2) 0.022;

3) 0.025;

4) 0.011.

18. Длина отрезка неопределенности после 3-х итераций по методу золотого сечения, если минимум отделен на отрезке [5,7], равна…

1) 0.472; *

2) 0.634;

3) 0.111;

4) 0.268.

19. Длина отрезка неопределенности после 5-ти итераций по методу дихотомии ( 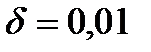), если минимум отделен на отрезке [5,7], равна…

1) 0.082; *

2) 0.180;

3) 0.016;

4) 0.072.

20. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [2,4], методом золотого сечения с точностью 10^-4 равно…

1) n = 20; *

2) n = 16;

3) n = 25;

4) n = 19.

21. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [0,1], методом золотого сечения с точностью 10^-3 равно…

1) n = 15; *

2) n = 19;

3) n = 10;

4) n = 14.

22. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [0,1], методом дихотомии ( ) с точностью 10^-3 равно…

1. n = 11; *

2. n = 10;

3. n = 14;

4. n = 12.

23. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [1,3], методом дихотомии ( 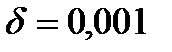) с точностью 10^-2 равно…

1) n = 8; *

2) n = 7;

3) n = 9;

4) n = 10.

24. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [6,8], методом золотого сечения с точностью 10^-3 равно…

1) n = 15; *

2) n = 14;

3) n = 18;

4) n = 19.

25. Теоретическое количество итераций, необходимое для локализации точки минимума, отделенного на отрезке [1,2], методом дихотомии ( 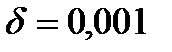) с точностью 10^-2 равно…

1) n = 6; *

2) n = 7;

3) n = 9;

4) n = 8.

Это HTML версия файла http://onemove.ru/get/34975/.

G o o g l e автоматически создает HTML версии документов при сканировании Интернета.Page 1

Вопрос: В методе прямоугольников подынтегральная функция заменяется

интерполяционным многочленом

Ответ: 0-й степени

Вопрос: Для функции f(x,y)=

, матрица Гессе имеет следующий вид

Ответ:

Вопрос: При использовании n+1 узла таблицы, интерполяционный полином Лагранжа

является полиномом

Ответ: n –ой степени

Вопрос: Метод одномерной оптимизации, где конечная длина отрезка неопределенности

равна

- есть метод

Ответ: дихотомии

Вопрос: Термином, используемым при решении задачи аппроксимации, является

Ответ: невязка

Вопрос: Отличие численного метода наискорейшего спуска состоит в том, что поиск

значения

на каждой итерации происходит

Ответ: одним из численных методов одномерной оптимизации

Вопрос: Решение системы из двух уравнений относительно a0, a1

позволяет найти коэффициенты аппроксимирующего многочлена

Ответ: первого порядка

Вопрос: Прогнозирование поведения функции за пределами интервала заданных точек это

Ответ: эстраполяция

Вопрос: Оценку погрешности решения методов Рунге-Кутты проводят

Ответ: по правилу Рунге

Вопрос: В случае применения метода наименьших квадратов для определения

коэффициентов эмпирической формулы,

имеющей вид алгебраического многочлена степени m, система уравнений будет состоять из

Ответ: m + 1 уравнений

Вопрос: Точкой стационарности называется точка, в которой

Ответ: градиент функции равен нулю

Вопрос: В методе наименьших квадратов вектор коэффициентов аппроксимирующей

функции определяется

из условия минимизации

Ответ:

Вопрос: Используя одни и те же узлы интерполяции, построить несколько

интерполяционных полиномов

Ответ: нельзя

Вопрос: Уточнить корень нелинейного уравнения графическим методом

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 1 из 20

28.12.2010 20:34Page 2

Ответ: нельзя

Вопрос: Отделение корней нелинейного уравнения сводится к нахождению отрезков, в

пределах которых функция

Ответ: монотонна и изменяет свой знак

Вопрос: Не существует метода интегрирования

Ответ: метода средних трапеций

Вопрос: Суть методов одномерной оптимизации заключается

Ответ: в том, что на каждой итерации отрезок неопределенности уменьшается и стягивается к

точке минимума

Вопрос: Точка x для которой выполняется равенство

=0 называется

Ответ: стационарной точкой функции

Вопрос:

- эта формула является формулой для определения очередного

значения функции по методу

Ответ: Рунге-Кутты 1-го порядка

Вопрос: Термин - «метод расходится» означает

Ответ: очередное приближение отдаляется от корня уравнения

Вопрос: Единственность решения задачи полиномиального интерполирования

обеспечивается

Ответ: выполнением условий интерполирования в n+1 точке из интервала приближения (n –

порядок полинома)

Вопрос: В общем виде ОДУ можно представить следующим образом

Ответ:

Вопрос: Изменение степени интерполяционного полинома на единицу (добавление в таблицу

значений функции одного узла)

ведет к полному пересчету

Ответ: формулы Лагранжа

Вопрос: в методе Эйлера для вычисления интеграла используется метод

Ответ: левых прямоугольников

Вопрос: При использовании формулы Лагранжа располагать узлы интерполяции можно

Ответ: в произвольном порядке

Вопрос: Метод правых прямоугольников имеет порядок точности, равный

Ответ: 1

Вопрос: Стационарная точка - это точка,

Ответ: в которой f'(x)=0

Вопрос: Термин, который относится к методам решения нелинейных уравнений это

Ответ: итерация

Вопрос: За начальное приближение при решении нелинейного уравнения методом итераций

принимают

Ответ:

, если

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 2 из 20

28.12.2010 20:34Page 3

Вопрос: Формула погрешности

, где

применятся в

Ответ: методе трапеций

Вопрос: Точность метода дихотомии повышается, если

Ответ: уменьшить заданную погрешность

Вопрос: Вторая интерполяционная формула Ньютона используется, когда точка

интерполяции находится

Ответ: в конце таблицы с равноотстоящими узлами

Вопрос: Правилом выбора неподвижной точки при решении нелинейного уравнения

методом хорд является

Ответ:

Вопрос: При использовании n+1 узлов таблицы, интерполяционный полином Ньютона

является полиномом

Ответ: n –ой степени

Вопрос: Интерполяционный полином наименьшей степени, это полином степени

Ответ: 0

Вопрос: Погрешность методов Рунге-Кутты 4-го порядка пропорциональна величине

Ответ:

Вопрос: Метод численного интегрирования, в котором подынтегральная функция

заменяется полиномом нулевой степени,

называется

Ответ: методом прямоугольников

Вопрос: К начальным условиям при решении ОДУ 1-го порядка численными методами

относятся

Ответ:

Вопрос: Чтобы повысить точность определения точки минимума в методах многомерной

оптимизации надо

Ответ: уменьшить допустимую погрешность

Вопрос: Погрешность метода Эйлера пропорциональна

Ответ: шагу, возведенному в квадрат

Вопрос: Интерполирующая функция это

Ответ: функция, на которую заменяют таблично заданную функцию

Вопрос: Метод одномерной оптимизации, где значение целевой функции на каждой

итерации вычисляется один раз

Ответ: золотого сечения

Вопрос: Метод левых прямоугольников имеет порядок точности, равный

Ответ: 1

Вопрос: Корень x на отрезке [a;b] существует, если

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 3 из 20

28.12.2010 20:34Page 4

Ответ: f(x) на концах отрезка имеет разные знаки

Вопрос: В методах одномерной оптимизации при переходе к следующей итерации часть

отрезка можно отбросить,

считая, что там нет минимума функции, потому что

Ответ: функция на отрезке неопределенности унимодальна

Вопрос: Определённый интеграл в методах численного интегрирования вычисляется по

формуле

Ответ:

Вопрос: Дана подынтегральная функция y=5.

Численный метод, с интерполяционным многочленом наименьшей степени, позволяющий

вычислить интеграл без ошибки, называется

Ответ: метод средних прямоугольников

Вопрос: Система нормальных уравнений содержит 3 уравнения, если проводится

аппроксимация.

Ответ: полиномом 2-й степени

Вопрос: За начальное значение шага ( ) в методе ГДШ принимается

Ответ: 0< <1

Вопрос: Численное значение интеграла

равно

Ответ: площади, ограниченной кривой

и двумя ординатами в точках а и b

Вопрос: Градиентные методы – это методы, в которых движение к точке минимума

совпадает с направлением

Ответ: вектора антиградиента функции

Вопрос: Зависимость между числом узлов интерполяции и степенью интерполяционного

многочлена состоит в том, что

Ответ: степень интерполяционного многочлена на единицу меньше числа узлов

Вопрос: Из перечисленных методов какой НЕ относится в методам многомерной

оптимизации

Ответ: Рунге-Кутты

Вопрос: Для построения аппроксимирующего многочлела 3-й степени должно быть как

минимум

Ответ: четыре узла

Вопрос: Полином, построенный по таблично заданной функции,

обеспечивающий полное совпадение в используемых для его построения точках это

Ответ: интерполирующий полином

Вопрос: Аппроксимировать функцию, заданную таблицей из 30-ти точек, многочленом

квадратичной функцией

Ответ: можно

Вопрос: В методе золотого сечения на каждой итерации отрезок неопределенности

уменьшается

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 4 из 20

28.12.2010 20:34Page 5

Ответ: в 1.618 раз

Вопрос: Метод двойного просчета служит для

Ответ: вычисления интеграла с заданной точностью

Вопрос: Процесс решения нелинейного уравнения состоит из

Ответ: двух этапов

Вопрос: Задача численного интегрирования требует выполнения интерполяции при

Ответ: вычислении элементарного интеграла

Вопрос: Вектор градиента это

Ответ: вектор, состоящий из первых частных производных целевой функции

Вопрос: сходимтся к корня, если

Ответ:

Вопрос: Метод трапеций имеет порядок точности, равный

Ответ: 2

Вопрос: Аппроксимация это

Ответ: получение функции более простого вида, описывающей исходную с достаточной степенью

точности

Вопрос: Очередная точка решения ОДУ методом Рунге-Кутты вычисляется на основании

Ответ: одного предыдущего значения функции

Вопрос: Необходимым условием существования корня нелинейного уравнения на отрезке

[a;b] является

Ответ:

Вопрос: Единственность решения полиномиального интерполирования обеспечивается

Ответ: выполнением условия интерполирования во всех узлах интерполяции

Вопрос: Интерполяционных полиномов Лагранжа степени n существует

Ответ: один

Вопрос: Всякий глобальный минимум выпуклой функции является одновременно и

Ответ: локальным

Вопрос: Способы определения параметров эмпирической формулы - это

Ответ: метод наимельших квадратов

Вопрос: На отрезке [a;b] имеется хотя бы один корень, если

Ответ:

Вопрос: Метод одномерной оптимизации, который обладает наименьшей трудоемкостью

Ответ: метод золотого сечения

Вопрос: Методы Рунге-Кутты решения дифференциальных уравнений являются

Ответ: одношаговыми методами

Вопрос: Требуемая точность решения ОДУ достигается применением в расчетах метода

Ответ: автоматического выбора шага

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 5 из 20

28.12.2010 20:34Page 6

Вопрос: Величина шага спуска в аналитическом методе наискорейшего спуска выбирается

из условия

Ответ:

Вопрос: Меньшее количество интервалов разбиения при вычислении интеграла с заданной

точностью потребуется для

Ответ: метода Симпсона

Вопрос: В качестве начального приближения при решении нелинейного уравнения методом

хорд выбирается

Ответ:

Вопрос: Интерполяционных полиномов степени n существует

Ответ: один

Вопрос: В градиентном методе с дроблением шага (ГДШ) на каждой итерации шаг

Ответ: уменьшается в 2 раза

Вопрос: Если

, то шаг для следующей точки

Ответ: выбирается равным h

Вопрос: Решение системы из четырёх уравнений относительно a0, a1, a2, a3

позволяет найти коэффициенты аппроксимирующего многочлена

Ответ: третьего порядка

Вопрос: В обыкновенном дифференциальном уравнении присутствуют

Ответ: производные разных порядков от одной переменной

Вопрос: В методе наискорейшего спуска (НС) на каждой итерации шаг выбирается исходя

из условия

Ответ: минимума целевой функции

Вопрос: Обеспечить вычисление интеграла с заданной точностью можно, используя

Ответ: метод двойного просчета

Вопрос: Основное достоинство метода золотого сечения

Ответ: на каждой итерации значение целевой функции вычисляется только один раз

Вопрос: На каждой итерации в методе ГДШ шаг уменьшается

Ответ: в 2 раза

Вопрос: Решение системы из трёх уравнений относительно a0, a1, a2

позволяет найти коэффициенты аппроксимирующего многочлена

Ответ: второго порядка

Вопрос: Погрешность метода Рунге-Кутты четвёртого порядка

Ответ: меньше, чем методов 1-го и 2-го

Вопрос: Метод половинного деления всегда находит корень нелинейного уравнения f(x)=0,

если

Ответ: выполнено условие существования и единственности корня на отрезке

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 6 из 20

28.12.2010 20:34Page 7

Вопрос: Определенный интеграл в случае, если подынтегральная функция задана таблицей

с переменным шагом

Ответ: вычисляется как сумма интегралов с постоянным шагом

Вопрос: С увеличением количества узлов аппроксимации точность аппроксимации

Ответ: увеличивается

Вопрос: Глобальный минимум является

Ответ: наименьшим из локальных

Вопрос: Метод наименьших квадратов предназначен для

Ответ: аппроксимации функции

Вопрос: Отрезком неопределённости называется

Ответ: отрезок, на котором локализован единственный минимум

Вопрос: При решении нелинейного уравнения целесообразно выбирать отрезок, на котором

отделен корень небольшой длины в методе

Ответ: метод Ньютона

Вопрос: Задача Коши для дифференциального уравнения первого порядка имеет

Ответ: единственное решение

Вопрос: Шаг интерполяции это

Ответ: расстояние между узлами интерполяции

Вопрос: Условие существования минимума для функции от двух переменных это

Ответ: положительная определенность матрицы вторых производных

Вопрос: В случае применения метода наименьших квадратов для определения

коэффициентов эмпирической формулы,

имеющей вид алгебраического многочлена второй степени, система уравнений будет

состоять из

Ответ: 3 уравнений

Вопрос: При вычислении элементарного интеграла по методу прямоугольников точки

соединяются

Ответ: прямой

Вопрос: Формула

предназначена для вычисления элементарного

интеграла по формуле

Ответ: Симпсона

Вопрос: На этапе уточнения корней нелинейного уравнения определяют

Ответ: значение корня с заданной степенью точности

Вопрос: Замена таблично заданной функции y=f(x) другой функцией g(x), такой, что

g(xi)=fxi) (i=0,1,2,…,n), это -

Ответ: интерполяция

Вопрос: На каждой итерации в методе наискорейшего спуска шаг выбирается исходя из

условия

Ответ: минимума целевой функции

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 7 из 20

28.12.2010 20:34Page 8

Вопрос: Методы Рунге-Кутты называют одношаговыми методами, потому что

Ответ: для вычисления очередной точки решения используются сведения только о предыдущей

точке

Вопрос: На этапе отделения корней нелинейного уравнения используется

Ответ: графический метод

Вопрос: Метод решения нелинейного уравнения, обладающий квадратичной сходимостью

это

Ответ: метод Ньютона

Вопрос: Метод интегрирования, который наилучшим образом подходит для вычисления

интеграла линейной функции,

называется

Ответ: методом трапеций

Вопрос: Чтобы повысить точность метода прямого перебора надо

Ответ: задать меньшее значение погрешности

Вопрос: Аппроксимировать функцию, заданную таблицей из 20-ти точек, многочленом

квадратичной функцией

Ответ: можно

Вопрос: Траектория спуска это

Ответ: последовательность точек

, получаемых методом спуска

Вопрос: Из перечисленных методов к методам многомерной оптимизации относится

Ответ: в списке нет правильного ответа

Вопрос: Для построения аппроксимирующего многочлена 2-й степени должно быть как

минимум

Ответ: три узла

Вопрос: Чем больше табличных значений функции использовано при построении

аппроксимирующего многочлена

Ответ: тем выше его степень

Вопрос: При использовании формулы Лагранжа добавление дополнительного узла

Ответ: потребует полного пересчета коэффициентов

Вопрос: Использование дополнительной точки исходных данных, расположенной внутри

отрезка [x0;xn] в формуле Лагранжа

Ответ: увеличит точность

Вопрос: Критерием близости аппроксимируемой и аппроксимирующей функции при

использовании метода наименьших квадратов служит

Ответ: минимум суммы квадратов отклонений аппроксимируемой и аппроксимирующей функций

Вопрос: По количеству параметров задачи оптимизации делятся на

Ответ: одномерные и многомерные

Вопрос: Пусть в качестве аппроксимирующей функции выбрана линейная зависимость

,

тогда критерий минимизации имеет вид

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 8 из 20

28.12.2010 20:34Page 9

Ответ:

Вопрос: Линия уровня это

Ответ: множество точек, для которых целевая функция f(x1,x2) принимает постоянное значение

Вопрос: Линейная функция формул Рунге-Кутты для решения ОДУ первого порядка

выглядит следующим образом

,

коэффициентам P1,P2,…,Pn подбирают значения, которые обеспечивают

Ответ: минимальную погрешность

Вопрос: Нелинейное уравнение это

Ответ: алгебраическое или трансцендентное уравнение

Вопрос: Функция, для которой решается задача оптимизации, называется

Ответ: целевой

Вопрос: За решение задачи одномерной оптимизации при выполнении условия

как правило принимают

Ответ: середину отрезка [ai;bi]

Вопрос: При решении ОДУ по сравнению с методом Эйлера, метод «прогноза и коррекции»

Ответ: требует меньшее количество итераций для обеспечения заданной точности

Вопрос: Замена некоторой функции y=f(x) другой функцией g(x,a0,a1,…,a n) таким образом,

чтобы отклонение g(x,a0,a1,…,an) от f(x)

удовлетворяло в некоторой области определенному условию называется

Ответ: аппроксимацией

Вопрос: Модуль градиента показывает

Ответ: скорость возрастания функции

Вопрос: Если поменять у целевой функции знак на противоположный, то с помощью

методов одномерной оптимизации найдем

Ответ: максимум функции

Вопрос: Формула (b-a)/n служит для определения (n – число разбиений)

Ответ: шага интегрирования

Вопрос: Высшей степенью точности обладает

Ответ: метод Симпсона

Вопрос: Метод решения нелинейного уравнения, который требует более близкого к корню

начального значения это

Ответ: метод Ньютона

Вопрос: Функция, приближенно описывающая таблично заданную функцию, это

Ответ: аппроксимирующая функция

Вопрос: В методе дихотомии на каждой итерации отрезок неопределенности уменьшается

Ответ: почти в 2 раза

Вопрос: Кубатурой называется

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 9 из 20

28.12.2010 20:34Page 10

Ответ: вычисление интеграла 2-х переменных

Вопрос: Численные методы решения ОДУ позволяют

Ответ: вычислить приближенные значения искомого решения y(x) на некоторой сетке значений

аргументов

Вопрос: Применение переменного шага является

Ответ: возможным во всех методах Рунге-Кутты

Вопрос: Этап «отделения корней» нелинейного уравнения заключается в

Ответ: нахождении отрезков, внутри которых находится строго один корень

Вопрос: Достаточным условием существования минимума функции нескольких переменных

является

Ответ: матрица вторых производных должна быть положительно определена

Вопрос: Чтобы выбрать x0 в качестве начального приближения в методе Ньютона

необходимо, чтобы в этой точке

Ответ: функция и вторая производная имели одинаковые знаки

Вопрос: Порядок методов Рунге-Кутты определяется

Ответ: количеством оставленных членов ряда при разложении функции в ряд Тейлора

Вопрос: Коэффициенты золотого сечения при решении задачи одномерной оптимизации

равны

Ответ: 0.382 и 0.618

Вопрос: Точность метода прямого перебора повышается, если

Ответ: нет правильного ответа

Вопрос: Точность численного интегрирования зависит

Ответ: от величины шага интегрирования

Вопрос: В методе наименьших квадратов параметры аппроксимирующей функции

определяются из условия

Ответ: минимума суммы квадратов отклонений аппроксимирующей функции от

аппроксимируемой

на конечном множестве точек из интервала приближения

Вопрос: К методам уточнения корня нелинейного уравнения не относится

Ответ: графический метод

Вопрос: Шаг интегрирования (h), в формуле прямоугольников равен

Ответ: h=xi+1-xi

Вопрос: Методы спуска применяются для минимизации функций только от

Ответ: нескольких переменных

Вопрос: В методе НСЧ значение шага находят из отрезка

Ответ: [0;1]

Вопрос: Правилом выбора итерирующей функции при решении нелинейного уравнения

методом итераций является

Ответ:

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 10 из 20

28.12.2010 20:34Page 11

Вопрос: Если интерполируемая функция f(x) задана в (n+1) равноотстоящих узлах,

то для ее интерполяции удобнее использовать

Ответ: формулы Ньютона

Вопрос: Наименьшее значение функции в некоторой окрестности это

Ответ: локальный минимум

Вопрос: Погрешность метода Эйлера связана с величиной шага интегрирования

отношением

, где -

Ответ: произвольная постоянная

Вопрос: Дана подынтегральная функция y=5x

Метод численного интегрирования,

который дает наиболее точный результат

Ответ: метод Симпсона

Вопрос: Обыкновенное дифференциальное уравнение это

Ответ: дифференциальное уравнение от одной переменной

Вопрос: К методам отделения корня нелинейного уравнения не относится

Ответ: метод итераций

Вопрос: Важным для практического применения показателем, который определяется

порядком метода ОДУ, является

Ответ: количество используемых в формуле производных

Вопрос: График функции на отрезке [a;b] пересекает ось ОХ только один раз, если

выполняется условие

Ответ:

Вопрос: Формула погрешности

, где

применятся в

Ответ: методе средних прямоугольников

Вопрос: Модуль вектора антиградиента в точке минимума равен

Ответ: 0

Вопрос: Уменьшение числа разбиений влияет на погрешность интегрирования так, что она

Ответ: увеличится

Вопрос: Дана подынтегральная функция f(x)=x

.

Численный метод, позволяющий вычислить интеграл без ошибки, называется

Ответ: методом Симпсона

Вопрос: При решении нелинейного уравнения малая скорость сходимости характерна для

метода

Ответ: половинного деления

Вопрос: В каком методе для достижения одного и того же значения погрешности требуется

меньше итераций

Ответ: дихотомии

Вопрос: общая формула для оценки погрешности решения ОДУ методами Рунге-Кутты

имеет вид

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 11 из 20

28.12.2010 20:34Page 12

Ответ:

Вопрос: Если функция f(x) непрерывна и монотонна на отрезке [a;b] и принимает на концах

отрезка значения разных знаков,

то на отрезке [a;b] содержится

Ответ: 1 корень

Вопрос: Численное решение ОДУ представляет собой таблицу значений искомой функции

для заданной последовательности аргументов,

называется

Ответ: шагом интегрирования

Вопрос: Наиболее популярными среди классических одношаговых методов решения ОДУ

являются методы Рунге-Кутты

Ответ: четвертого порядка>

Вопрос: В методе наименьших квадратов параметры апроксимирующей функции a0, a1,...,an

определяются исходя из

Ответ: условия минимума суммы квадратов отклонений этой функции от эксперементальных

данных

Вопрос: Поиск очередной точки траектории спуска в методе наискорейшего спуска

осуществляется

Ответ: в направлении антиградиента

Вопрос: Формула

служит для определения (n – число разбиений)

Ответ: шага интегрирования

Вопрос: Формула

предназначена для вычисления элементарного интеграла по

формуле

Ответ: трапеций

Вопрос: Для построения аппроксимирующего многочлела 1-й степени должно быть как

минимум

Ответ: два узла

Вопрос: Начальная точка при решении задачи многомерной оптимизации выбирается

Ответ: из области существования функции

Вопрос: Метод средних прямоугольников имеет порядок точности, равный

Ответ: 2

Вопрос: Метод решения нелинейного уравнения, в результате которого получается

последовательность вложенных отрезков это

Ответ: метод половинного деления

Вопрос: Геометрической интерпретацией общего решения ОДУ

является

Ответ: семейство непересекающихся интегральных кривых

Вопрос: Длина отрезка неопределенности в методе золотого сечения сокращается на каждой

итерации

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 12 из 20

28.12.2010 20:34Page 13

Ответ: нет правильного ответа

Вопрос: Нахождение возможно более узкого отрезка, содержащего только один корень

уравнения, называется

Ответ: отделением корней

Вопрос: Узлы интерполяции это

Ответ: значения xi (i = 0,1,2,…,n)

Вопрос: На скорость сходимости метода дихотомии вид функции

Ответ: не влияет

Вопрос: Метод одномерной оптимизации, требующий проведения большего количества

итераций для достижения заданной точности

Ответ: метод прямого перебора

Вопрос: При решении задачи численного интегрирования интерполяция используется

Ответ: на этапе вычисления элементарного интеграла

Вопрос: Метод, в котором подынтегральная функция заменяется полиномом наименьшей

степени, называется

Ответ: методом прямоугольников

Вопрос: Модифицированный метод Эйлера относится к методам Рунге-Кутты решения ОДУ

Ответ: 2-го порядка

Вопрос: При уменьшении количества узлов интерполяции точность интерполяции

Ответ: уменьшается

Вопрос: Условие окончания итерационного процесса по отысканию точки минимума в

методах спуска это

Ответ: модули частных производных по всем переменным меньше заданной точности

Вопрос: Уменьшение шага интегрирования при использовании методов Рунге-Кутты

Ответ: уменьшает погрешность

Вопрос: Метод Эйлера называют методом Рунге-Кутты первого порядка, потому что

Ответ: для получения очередной точки проводится одно уточнение

Вопрос: Не бывает методов Рунге-Кутта

Ответ: 0-го порядка

Вопрос: Интерполируемая функция это

Ответ: функция, заданная таблично

Вопрос: Наиболее рациональным способом выбора параметра в методе дихотомии

является

Ответ:

Вопрос: Глобальный минимум это

Ответ: наименьший из минимумов в области допустимых значений

Вопрос: Первым приближением к корню, отделенному на отрезке [a;b],

при решении нелинейного уравнения методом половинного деления служит

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 13 из 20

28.12.2010 20:34Page 14

Ответ:

Вопрос: Метод дихотомии гарантирует отыскание минимума с заданной точностью, если

Ответ: правильно выбран отрезок неопределенности

Вопрос: В методе трапеций подынтегральная функция заменяется интерполяционным

многочленом

Ответ: 1-й степени

Вопрос: Вектор антиградиента направлен

Ответ: в сторону наискорейшего убывания целевой функции

Вопрос: Аналитическое решение ОДУ 1-го порядка это

Ответ: функция y(x), которая при подстановке в уравнение обращает его в тождество

Вопрос: Если для всей области допустимых значений выполняется неравенство

то

точка x* являеться точкой

Ответ: глобального минимума

Вопрос: Метод Эйлера имеет порядок точности

Ответ: первый

Вопрос: В методе наименьших квадратов при линейной аппроксимации эмпирическая

формула будет получена из

Ответ: 2 уравнений

Вопрос: В точке корня функция равна

Ответ: нулю

Вопрос: Поиск минимума в методе дихотомии начинается с выбора на отрезке

неопределённости

Ответ: двух симметричных относительно середины точек

Вопрос: Количество интервалов разбиения, кратное двум, необходимо выбирать для

вычисления интеграла

Ответ: методом Симпсона

Вопрос: Шаг равномерной сетки изменения х на отрезке [a;b]

вычисляется по формуле (n – число узлов)

Ответ:

Вопрос: За точку минимума при выполнении условия |bn-an| можно принять

Ответ: любую точку конечного отрезка [anbn]

Вопрос: Метод одномерной оптимизации, который обладает более высокой скоростью

сходимости

Ответ: метод дихотомии

Вопрос: Если точка интерполяции Х находится в начале таблицы с равноотстоящими

узлами,

то для построения интерполяционного полинома с возможно меньшей погрешностью

используется

Ответ: первая формула Ньютона

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 14 из 20

28.12.2010 20:34Page 15

Вопрос: Формула погрешности

, где

применятся в

Ответ: методе Симпсона

Вопрос: При увеличении количества узлов интерполяции точность интерполяции

Ответ: увеличивается

Вопрос: Методом оптимизации можно найти глобальный минимум, если

Ответ: глобальный минимум совпадает с локальным

Вопрос: Критерий аппроксимации показывает

Ответ: числовую меру близости исходной и аппроксимирующей функций

Вопрос: Величина шага на каждой итерации в методе наискорейшего спуска определяется

из условия

Ответ: минимума функции

Вопрос: Оптимальное значение функции это

Ответ: наилучшее

Вопрос: Общим решением ОДУ

является

Ответ:

Вопрос: Метод Симпсона имеет порядок точности, равный

Ответ: 4

Вопрос: Первая производная от целевой функции на отрезке неопределенности должна

Ответ: не убывать

Вопрос: При решении ОДУ, если отрезок интегрирования не велик, то методы Рунге-Кутты

Ответ: эффективны и обеспечивают достаточно высокую точность

Вопрос:

- это

Ответ: формула Лагранжа

Вопрос: Этапы решения нелинейного уравнения называются

Ответ: отделение корней и уточнение отделенного корня

Вопрос: Если на значения параметров оптимизации существуют ограничения, то задача

оптимизации называется

Ответ: условной

Вопрос: Шаг интегрирования - это

Ответ: расстояние между значениями xi и xi+1

Вопрос: Метод, не предназначенный для решения нелинейных уравнений это

Ответ: метод прямоугольников

Вопрос: Метод одномерной оптимизации, где проводится большее количество вычислений

функции для достижения необходимой точности

Ответ: метод дихотомии

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 15 из 20

28.12.2010 20:34Page 16

Вопрос: В модифицированном методе Эйлера на каждом шаге

необходимо

вычислять

Ответ: два раза

Вопрос:

является

Ответ: обыкновенным дифференциальным уравнением 1-го порядка

Вопрос: для применения формул Рунге-Кутты для решения ОДУ первого порядка к

уравнениям n-го порядка

Ответ: уравнение приводится к системе из n уравнений первого порядка

Вопрос: Метод хорд применяется на этапе

Ответ: уточнения корня

Вопрос: Вид функции на скорость сходимости метода дихотомии

Ответ: не влияет

Вопрос: При решении задачи одномерной оптимизации более высокой скоростью

сходимости обладает

Ответ: метод дихотомии

Вопрос: Метод решения нелинейного уравнения сходится, если

Ответ: за конечное число итераций корень найден с заданной точностью

Вопрос: Утверждение, что вид функции влияет на скорость сходимости метода дихотомии

Ответ: неверно

Вопрос: Метод одномерной оптимизации, где длину конечного интервала неопределенности

вычисляют по следующей формуле

Ответ: дихотомии

Вопрос: Метод, где интервал неопределенности делится на некоторое число равных частей

с последующим вычислением значений целевой функции в точках разбиения -есть

Ответ: нет правильного ответа

Вопрос: Основное условие интерполяции это

Ответ: полное совпадение значений интерполируемой и интерполирующих функций во всех узлах

интерполяции

Вопрос: Частным решением ОДУ

является

Ответ:

Вопрос: Методы одномерного поиска применяются для

Ответ: унимодальных функций

Вопрос: Численное значение интеграла функции одной переменной называют

Ответ: квадратурой

Вопрос: Если при решении задачи одномерной оптимизации количество независимых

переменных n=1, то это

Ответ: одномерная оптимизация

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 16 из 20

28.12.2010 20:34Page 17

Вопрос: Конечная длина отрезка неопределенности при использовании метода золотого

сечения равна

Ответ:

Вопрос: Численное значение интеграла

равно

Ответ: площади, ограниченной кривой f(x), осью 0x и двумя ординатами в точках a и b

Вопрос: Цель двойного просчёта состоит в том, чтобы в каждой точке решения значения

погрешности

Ответ: отличались на величину, не превышающую заданную величину погрешности

Вопрос: В методах одномерной оптимизации при переходе к следующей итерации часть

отрезка [a;b]

можно отбросить, потому что

Ответ: на отрезке [a;b] целевая функция унимодальная

Вопрос: Система нормальных уравнений содержит 2 уравнения, если проводится

аппроксимация

Ответ: полиномом 1-й степени

Вопрос: При вычислении элементарного интеграла по методу Симпсона точки соединяются

Ответ: параболой

Вопрос: Матрица

называется

Ответ: матрица Гессе

Вопрос: Численным решением ОДУ

является

Ответ: таблица значений искомой функции

Вопрос: В методах Рунге-Кутты, при вычислении значения искомой функции в очередной

точке

,

используется информация о

Ответ: предыдущей точке

Вопрос: Функция на отрезке унимодальная, если

Ответ: на выбранном отрезке функция имеет один экстремум

Вопрос: Шаг интегрирования – это

Ответ: расстояние между значениями xi и xsub>i+1

Вопрос: Чтобы повысить точность метода дихотомии надо

Ответ: уменьшить заданную погрешность

Вопрос: Погрешность интегрирования при уменьшении числа разбиений

Ответ: увеличится

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 17 из 20

28.12.2010 20:34Page 18

Вопрос: Группа методов одномерной оптимизации,

где на каждой итерации интервал неопределенности уменьшается и стягивается к точке

минимума

Ответ: одномерного поиска

Вопрос: Чтобы повысить точность метода золотого сечения необходимо

Ответ: задать меньшее значение погрешности

Вопрос: Чтобы с использованием метода наискорейшего спуска найти максимум функции

f(x1,x2) нужно

Ответ: заменить в расчетах знак у целевой функции на противоположный

Вопрос: Первая производная от целевой функции на отрезке неопределённости должна

Ответ: не убывать

Вопрос: Вид функции на скорость сходимости метода прямого перебора

Ответ: влияет

Вопрос: Задача нахождения максимума целевой функции сводится к задаче

Ответ: замены f(x) на –f(x)

Вопрос: В методе золотого сечения на каждой итерации функция вычисляется один раз,

потому что

Ответ: одно из значений функции не вычисляется, а переопределяется,

поскольку каждая из внутренних точек (х1 и х2) делят отрезок в соотношении золотого сечения

Вопрос: При решении задачи оптимизации используется функция, которая называется

Ответ: целевой

Вопрос: Начальное приближение к корню при решении нелинейного уравнения это

Ответ: значениe х, обеспечивающее сходимость метода уточнения корня

Вопрос: При вычислении элементарного интеграла по методу трапеции точки соединяются

Ответ: прямой

Вопрос: Дана подынтегральная функция y=5x.

Численный метод, с интерполяционным многочленом наименьшей степени, позволяющий

вычислить интеграл с наименьшей погрешностью называется

Ответ: метод трапеций

Вопрос: Корень нелинейного уравнения f(x)=0 это

Ответ: значение переменной х, обращающее уравнение в тождество

Вопрос: Необходимым условием существования экстремума функции F(x) на отрезке [a;b]

является

Ответ:

Вопрос: Чтобы методами одномерной оптимизации найти максимум функции, нужно

Ответ: поменять у целевой функции знак на противоположный

Вопрос: При решении задачи одномерной оптимизации меньшей трудоемкостью обладает

Ответ: метод золотого сечения

Вопрос: Метод численного интегрирования, в котором подынтегральная функция

заменяется квадратичным полиномом,

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 18 из 20

28.12.2010 20:34Page 19

называется

Ответ: методом Симпсона

Вопрос: При решении ОДУ методом «прогноза и коррекции» порядок точности

Ответ: второй

Вопрос: Процесс решения дифференциального уравнения называется

Ответ: интегрированием

Вопрос: Порядок ОДУ это

Ответ: наивысший порядок производной, входящей в состав уравнения

Вопрос: Метод одномерной оптимизации, требующий проведения меньшего количества

итераций

для достижения заданной точности результата, это

Ответ: метод дихотомии

Вопрос: Степень отличия приближенного числа от его точного значения это

Ответ: погрешность

Вопрос: Относительная погрешность выражается отношением

Ответ: абсолютной погрешности к модулю приближенного значения

Вопрос: К точным числам относятся

Ответ: натуральные

Вопрос: Числа, представленные в ПК как тип Single или Double относятся к классу

Ответ: дробных

Вопрос: Модуль разности между точным и приближенным значением это

Ответ: абсолютная погрешность

Вопрос: Погрешность, связанная с описанием математической моделью реального явления,

это

Ответ: погрешность задачи

Вопрос: Для представления чисел в памяти компьютера применяют два способа: с

фиксированной запятой и

Ответ: с плавающей запятой

Вопрос: Формат чисел с плавающей запятой является международным стандартом

представления

Ответ: вещественных чисел

Вопрос: Правильной записью приближенного числа является

Ответ:

Вопрос: Относительная погрешность числа измеряется

Ответ: в процентах или долях

Вопрос: Абсолютная точность представления вещественных чисел с фиксированной запятой

Ответ: одинакова в любой части диапазона

Вопрос: Погрешность, обусловленная выполнением действий над данными, полученными с

ограниченной точностью, это

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 19 из 20

28.12.2010 20:34Page 20

Ответ: неустранимая погрешность

Вопрос: Относительная точность представления вещественных чисел в ПК одинакова в

любой части диапазона

и зависит лишь от числа разрядов

Ответ: отводимых под мантиссу числа

Вопрос: Точность вещественного числа в ПК определяется

Ответ: количеством цифр в дробной части этого числа

Вопрос: Потери точности при записи десятичных дробей велики из-за того, что

Ответ: двоичный эквивалент числа получается с погрешностями

Вопрос: Дробь 1/3 в десятичной системе получится

Ответ: периодической

Вопрос: Точными числами являются

Ответ: 13

Вопрос: Абсолютная погрешность числа измеряется

Ответ: в тех же единицах измерения, что и само число

Вопрос: Формула для определения относительной погрешности числа это

Ответ:

file:///D:/документы jet/вынуть/экзамен инфа/6.1-6.8.html

Стр. 20 из 20

28.12.2010 20:34