КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перемножение матриц.
Число столбцов первого множителя должно равняться числу строк второго
Вопрос №4
Транспонирование матриц. Определитель и его свойства
Транспонированной матрицей назовем такую матрицу, у которой строки матрицы заменены на столбцы
Определителем матрицы называется число, которое получается при сложении произведений элементов матрицы, взятых либо с «+», либо с « - »
свойства:
- Определитель равен нулю, если матрица содержит 0 строку (столбец)
- Опр.матрицы равен 0, если она содержит одинак. Стр и столб
- Определитель матрицы равен определитель транспонированной матрицы
- Определитель матрицы изменит знак, сли поменять стр и стлб
- Если стр(стлб) определит. Матр. Представляет собой сумму двух чисел, то определитель равен сумме двух определителей
- Если стр(стлб) определит.кратен некоторому числу, это число можно вынести за знак опредеителя
7. Опр.матрицы не изм., если к любой стр(стлб) матрицы добавить др.строку(стлб) матрицы, умноженную на конст, не равн.0
Вопрос №5
Умножение матриц. Свойства умножения
Операция умножения двух матриц А и В определяется только для случая, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В
- Свойство ассоциативности умножения матриц
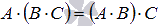 .
. - Два свойства дистрибутивности
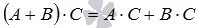 и
и  .
. - В общем случае операция умножения матриц некоммутативна
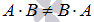 .
. - Единичная матрица Е порядка n на n является нейтральным элементом по умножению, то есть, для произвольной матрицы А порядка p на n справедливо равенство
 , а для произвольной матрицы А порядка n на p - равенство
, а для произвольной матрицы А порядка n на p - равенство 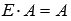 .
.
Вопрос №6
Обратная матрица. Необходимое и достаточное условие существования обратной матрицы
Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.
Доказательство.
1) Необходимость: так как 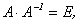 то
то  (теорема 3.1), поэтому
(теорема 3.1), поэтому 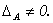
2) Достаточность: зададим матрицу  в следующем виде:
в следующем виде:
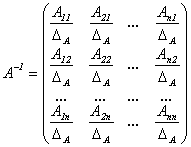 .
.
Тогда любой элемент произведения 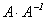 (или
(или 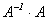 ), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны
), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны  Таким образом,
Таким образом,
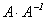 =
= 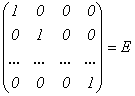 . Теорема доказана.
. Теорема доказана.
Вопрос №7
Линейная независимость элементов линейного пространства. Свойства линейной независимости
Набор элементов линейного пространства называется линейно-независимым, если из равенства нулю линейной комбинации следует, что она тривиальна
(Набор элементов линейного пространства называется лин-зав, если сущ нетривиальная лин.комб, равная нулю)
Cвойства:
1.Если среди элементов набора есть нулевой элемент пространства, то весь набор лин.зав
2. Если среди n-элементов есть m-зависимых, тогда весь набор зависим, следовательно, любое подмножество линейно-независим.множества набора лин-незав
Вопрос №8
Базис линейного пространства. Координаты элементов. Линейные операции
Набор элементов линейного пространства назыв. Базисом, если 1-эти элементы лин-незав, 2-любой элемент лин.пространства мб выражен их лин.комбинацией
Координатами элемента линейного пространства в некотором базисе называются коэффициенты разложения по этому базису.
Вопрос №9
СЛАУ. Решение системы. Виды систем
Системой линейных алгебраических уравнений порядка n называется выражение вида:


Решение СЛАУ:
СЛАУ имеет решение, если существует такой упорядоченный набор чисел Х, что при подставлении в систему он обращает все уравнения в тождества
Пример:  A=
A=  X=
X=  B=
B= 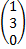 A*X=B
A*X=B
Типы СЛАУ:
СЛАУ совместна, если она имеет хотя бы одно решение; не совместна, если решений нет
СЛАУ называется определенной, если решение единственное, и неопределенной, если решений бесконечно много
Вопрос №10
Ранг матрицы. Элементарные преобразования матриц
Рангом матрицы называется max количество лин-незав строк(столб) матрицы
Элементарные преобразования:
1. Замена мест строк и столбцов (поменять их местами)
2. Транспонирование
3. Домножение стр(стлб) на НЕ нулевую конст
4. К любой стр.(стлб) добавить любую др.стр(стлб), умнож на не нулевую конст
Вопрос №11
Теорема Кронекера-Капелли. Исследование систем
Система уравнений является совместной тогда и только тогда, когда ранг расширенной матрицы АВ равен рангу матрицы А.
Rang AB = Rang A
- Если ранг матрицы А (Rang A) = числу совместных неизвестных переменных, то система определенная
- Если Rang A < n(n – кол-во неизвестных), то система неопределенная.
Вопрос №12
Геометрический вектор как элемент линейного пространства (линейные операции и их свойства)
Геометрический вектор –направленный отрезок.
- Сложение векторов:
Правило параллелограмма:суммой 2-ух вектором «а» и «в», имеющих общее начало, называется вектор «с», представляющий собой диагональ параллелограмма, построенного на векторах «а» и «в».
Правило треугольника: суммой векторов «а» и «в» называется вектор «с», проведенный из начала вектора «а» в конец вектора «в».
Свойства векторов: 1. а+в = в+а – свойство коммуникативности
2. (а+в)+с = а+(в+с) – свойство ассоциативности
3. а *0 = а – закон поглощения нуля.
- Разность векторов:
Разностью векторов «а» и «в» называется вектор «с», который в сумме с вектором «в» дает вектор «а»
- Умножение вектора на число
Произведением вектора «а» на число λ называется вектор «в», коллинеарным вектору «а», имеющий длину |в|=λ*|а|, и совпадающий по направлению с вектором «а», если λ положительная, и имеющий противоположное направление с вектором «а», если λ отрицательная.
Вопрос №13
Коллинеарность векторов. Необходимое и достаточное условие коллинеарности
Если 2 вектора лежат на 1 прямой или на параллельных прямых, то они называются коллинеарными.
Необходимое и достаточное условие коллинеарности векторов a = ( x, y, z ) и b = ( u, v, w ) :
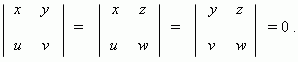
Вопрос №14
Компланарность векторов. Необходимое и достаточное условие компланарности
Вектора называются компланарными, если они лежат на 1 плоскости или на параллельных плоскостях.
Необходимое и достаточное условие компланарности векторов a = ( x, y, z ), b = ( u, v, w ) и c = ( p, q, r ) :

Вопрос №15
Базис на прямой, на плоскости и в пространстве. Координаты вектора в ортонормированном базисе
Базис на плоскости и в пространстве:
- Если вектора «а» и «в» не коллинеарны, тогда совокупность векторов с=αа+βв называется двухмерным векторным пространством [Е2], вектора «а» и «в» - базисы этого пространства, числа α и β – координаты вектора «с» в этом базисе.
- Если вектора «а», «в» и «с» не компланарны, то совокупность векторов d=αа+βв+γс назыв трехмерным пространством [Е3], где «а», «в» и «с» - базисы этого пространства, а числа α,β и γ – координаты вектора «d» в этом базисе.
Координаты вектора в ортонормированном базисе – это алгебраические проекции вектора на соответствующие оси
Вопрос №16
Скалярное произведение векторов. Свойства скалярного произведения. Угол между векторами
Скалярным произведением векторов «а» и «в» называется число, равное произведению длин этих векторов на косинус угла между ними.
а*в = |а| * |в| * cosФ - угол между векторами «а» и «в»
Свойства:
- а*в = в*а – свойство коммуникативности
- равенство 0 скалярного произведения свидетельствует о перпендикулярности этих векторов, и наоборот. а*в = 0 óа в
- Для любого вектора «а» произведение на самого себя = вектор «а»2
- а(в+с) = а*в + а*с
- (λ*а)в = λ(а*в)
Для вычисления cos угла между векторами:
x*y=|x| * |y| cosФ
cosФ = 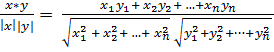
Вопрос №17
Скалярное произведение векторов. Необходимое и достаточное условие ортогональности векторов
Скалярным произведением векторов «а» и «в» называется число, равное произведению длин этих векторов на косинус угла между ними.
а*в = |а| * |в| * cosФ - угол между векторами «а» и «в»
Необходимое и дост усл:
Для перпендикулярности двух ненулевых векторов  и
и 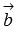 необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство .
необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство .
Доказательство.
Пусть векторы  и
и 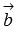 перпендикулярны. Докажем выполнение равенства
перпендикулярны. Докажем выполнение равенства 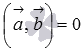 .
.
По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы  и
и 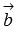 перпендикулярны, то угол между ними равен девяноста градусам, следовательно,
перпендикулярны, то угол между ними равен девяноста градусам, следовательно, 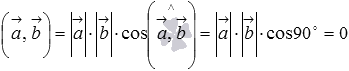 , что и требовалось доказать.
, что и требовалось доказать.
Переходим ко второй части доказательства.
Теперь считаем, что 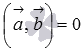 . Докажем, что векторы
. Докажем, что векторы  и
и  перпендикулярны.
перпендикулярны.
Так как векторы  и
и  ненулевые, то из равенства
ненулевые, то из равенства 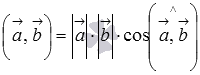 следует, что
следует, что  . Таким образом, косинус угла между векторами
. Таким образом, косинус угла между векторами  и
и 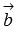 равен нулю, следовательно, угол
равен нулю, следовательно, угол  равен
равен 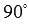 , что указывает на перпендикулярность векторов
, что указывает на перпендикулярность векторов  и
и 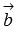 .
.
Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.
Вопрос №18
Скалярное произведение векторов в ортнонормированном пространстве. Длина вектора
Скалярным произведением векторов в ортонормированном базисе равно сумме попарных произведений соответствующих координат
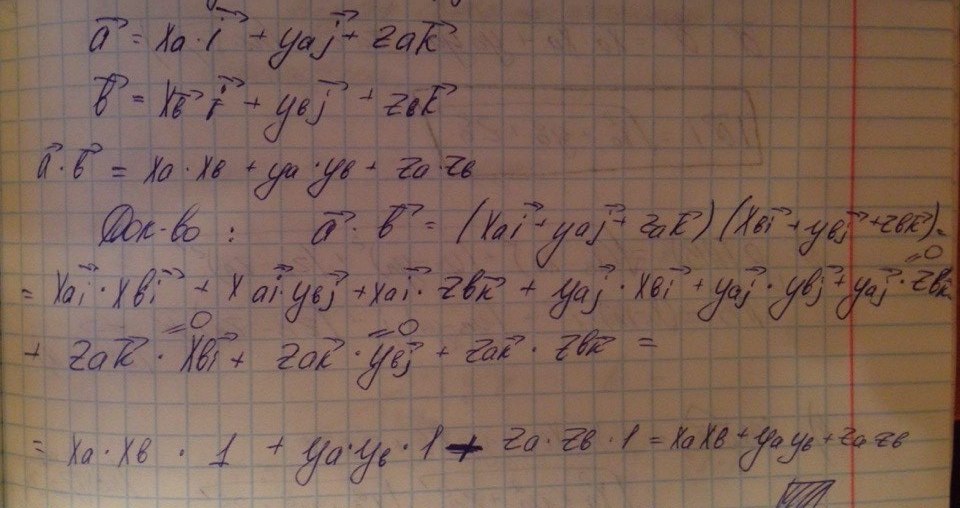
Длина вектора – это расстояние между точками а и b.
Вопрос №19
Прямая на плоскости. Взаимное расположение прямых на плоскости
· Две прямые на плоскости могут совпадать.
· Две прямые на плоскости могут пересекаться(Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными)

· Две прямые на плоскости могут быть параллельными. (Две прямые на плоскости называются параллельными, если они не имеют общих точек)

Вопрос №20
Прямая в пространстве. Взаимное расположение прямых в пространстве
· Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки).
· Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. 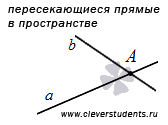
· В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. 
Вопрос №21
Плоскость. Взаимное расположение плоскостей
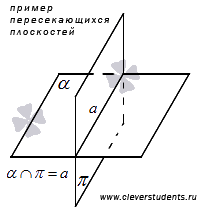
· Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.
· Две плоскости в пространстве могут пересекаться.
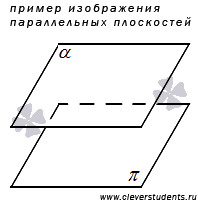
· Две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек.
Вопрос №22
Взаимное расположение прямой и плоскости в пространстве
Прямая и плоскость в пространство могут:
- а) не иметь общих точек;
- б) иметь ровно одну общую точку;
- в) иметь хотя бы две общие точки.
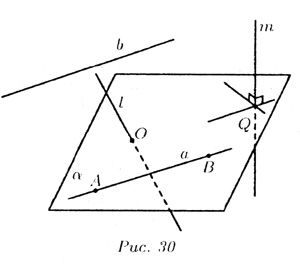
На рис. 30 изображены все эти возможности.
В случае а) прямая b параллельна плоскости 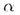 : b ||
: b || 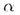 .
.
В случае б) прямая l пересекает плоскость 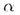 в одной точке О; l
в одной точке О; l 
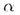 = О.
= О.
В случае в) прямая а принадлежит плоскости 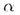 :
: 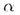
 а или а
а или а 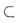
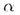 .
.
Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости 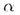 , то прямая параллельна плоскости
, то прямая параллельна плоскости 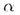 .
.
Вопрос №23
Способы задания множества. Множество и подмножество. Объединение множеств и его свойства

Множество А называют подмножеством В, если любой элемент А принадлежит В.

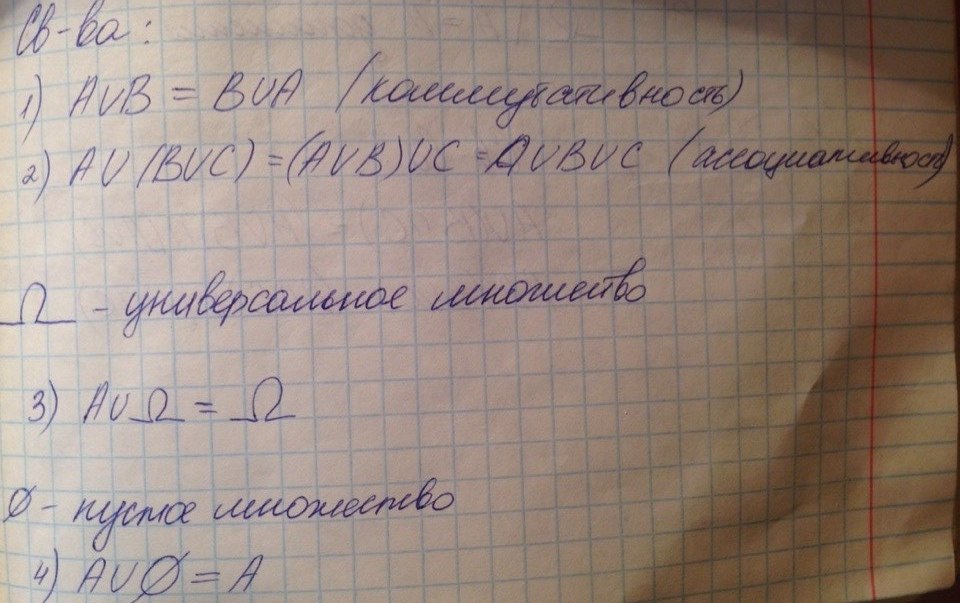
Вопрос №24
Множество. Пересечение множеств и его свойства. Числовые множества
Множеством элементов называется совокупность, отличающаяся друг от друга, но с другой стороны отличающихся от всех остальных элементов
Пересечением множеств A и B называется множество A B, которое состоит из тех и только тех элементов, которые принадлежат как множеству A, так и множеству B.
Множество А называют подмножеством В, если любой элемент А принадлежит В.
Вопрос №25
Множества на числовой прямой. Окрестность тоски, б – окрестность точки, окрестность бесконечно удаленной точки

Вопрос №26
Предел функции одной переменной. Графическое представление


Вопрос №27
Теорема об арифметических действиях над функциями, имеющими конечный предел
Пусть есть 2 ф-ции, имеющие конечн. предел в точке Х0, тогда предел суммы равен сумме пределов, множитель (константу) можно выносить за знак предела, предел произведения = произведению пределов, предел частного равен = частному пределов, если в знаменателе не 0.

Вопрос №28
Предел функции одной переменной. Теорема о единственности предела
Функция не может иметь в одной точке два различных предела.


Вопрос №29
Предел функции одной переменной. Теорема о сжатой переменной
f(x) , g(x) , φ(x) Ǝ O(Xo) : 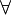 x
x  O(Xo)
O(Xo)
f(x) ≤ g(x) ≤ φ(x)  =
=  = A , A < ∞ => Ǝ
= A , A < ∞ => Ǝ 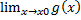 = A
= A
Если функции по бокам имеют одинаковый предел, то функция в середине имеет такой же предел.
Доказательство: 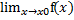 = A , A < ∞
= A , A < ∞
∀ ℇ > 0 Ǝ  > 0 ∀ x ∈ X : 0 < | X – Xo| < δ
> 0 ∀ x ∈ X : 0 < | X – Xo| < δ
| f(x) – A | < ℇ преобразуем - ℇ < f(x) – A < ℇ
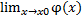 = A , A< ∞
= A , A< ∞
∀ ℇ > 0 Ǝ 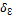 ´ > 0 : ∀ x ∈ X : 0 < | X – Xo| <
´ > 0 : ∀ x ∈ X : 0 < | X – Xo| < 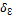 ´
´
| φ(x) – A | < ℇ преобразуем -ℇ < φ(x) – A < ℇ Получилось 2 дельта окрестность одной точки
Для всякого ℇ > 0 нашлась такая O ( 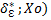
∀ x ∈ X : 0 < | X – Xo| < 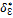
-ℇ < g(x) < ℇ => -ℇ < f(x) – A < ℇ => | g(x) – A | < ℇ , что и т.д.
Вопрос №30
Предел функции одной переменной. Теорема о предельном переходе в неравенстве
 = A , A< ∞
= A , A< ∞  = B
= B
Ǝ O (Xo) ; ∀ x ∈ O (Xo) f(x) < g(x) => A< B
Доказательство: Пусть f(x) < g(x) , A>B (от противного)
Рассмотрим  = A - B> 0
= A - B> 0
F(x) – g(x) < 0 в O(Xo)  <0 (по теореме о стабилизации знака)
<0 (по теореме о стабилизации знака)
А>B –противоречие => A<B
Вопрос №31
Бесконечно малые. Свойства бесконечно малых
Функция f(x) называют бесконечно малой величиной в точке х0 принадл. R U ±∞, если
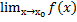 = 0
= 0
Свойства бмв:
- Суммадвух БМ в точке тоже является БМВ в этой точке
- Произведениедвух и более БМ в точке тоже является БМ в этой точке
- Частное от деления бмв на функцию, предел которой ≠ 0, есть величина бм.
Вопрос №32
Бесконечно малые. Эквивалентные БМ. Теорема об эквивалентных БМ
Функция f(x) называют бесконечно малой величиной в точке х0 принадл. R U ±∞, если
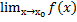 = 0
= 0
Эквивалентные БМ:
Две БМ эквивалентны, если их предел = 1

Теорема об эквивалентности БМ

Вопрос №33
Последовательность. Предел последовательности. Число е.
Последовательность – это функция натурального аргумента


Вопрос №34
Замечательные пределы
Первый замечательный предел
Пусть х измеряется в радианах, тогда 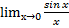 = 1
= 1
Док-во: Для выполнения доказательства проверим функцию под знаком lim на четность.
 (четная)
(четная)
Т.к. функция является четной, то доказательство выполняется в I четверти, с использованием окружности единичного радиуса.
| π/2 |
Sin x ===  = = 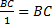 Tg x ===
Tg x ===  SΔ AOC < S сек AOC < SΔAOD
SΔ AOC =
SΔ AOC < S сек AOC < SΔAOD
SΔ AOC = 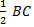 * OA = sin x *1 = * OA = sin x *1 = 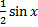 SΔ AOD =
SΔ AOD = 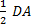 *OA = *OA = 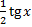 S сек AOC =
S сек AOC = 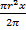 = = 

|
D
C
| X |
OA = 1
До множим все три части двойного неравенства на 2:
Sin x < x < 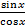
Поделим все 3 части на sin x: и поскольку sin x в I четверти «+», то знаки двойного неравенства сохранятся
1< 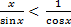
1< 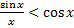
Выполним предельный переход в точу 0:

1 < 
Т.к. нет такой величины, которая одновременно была бы и больше и меньше 1, то естественно, что первый замечательный lim =1
Ч.т.д.
2-ой замечательный предел 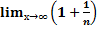 n = e
n = e
N=1 (1+  )1 = 2
)1 = 2
N=2 (1+  )2 = 2, 25
)2 = 2, 25
N=3 (1+  )3 = 2, 35
)3 = 2, 35
n→∞ e = 2,71826…
Вопрос №35
Теорема о связи функции, имеющей конечный предел и БМ

Вопрос №36
БМ и ББ. Теорема о связи ББ и БМ
Бесконечно малая и бесконечно большая величины:
Функция f(x) называют бесконечно малой величиной в точке х0 принадл. R U ±∞, если
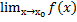 = 0
= 0
Функция f(x) называется бесконечно большойвеличиной в точке х0 принадл. R U ±∞, если 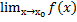 = ∞
= ∞
Теорема о связи бесконечно малых и бесконечно больших величин:
1. Пусть f(x) является бмв в точке х0, тогда  является ббв в этой точке
является ббв в этой точке
3. Пусть f(x) является ббв в точке х0, тогда  является бмв в этой точке
является бмв в этой точке



Вопрос №38
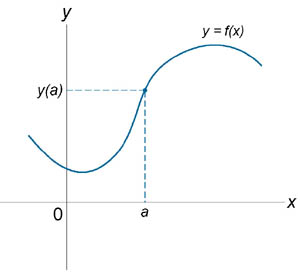
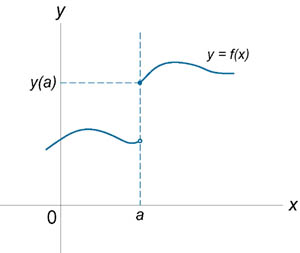
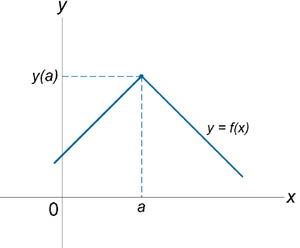
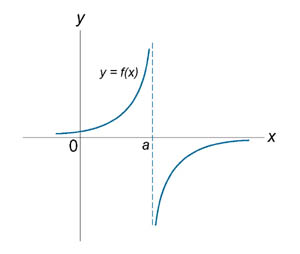
Непрерывность числовой ф-ии одной переменной в точке. Точки разрыва, классификация точек разрыва
Функция y=f(x) называется непрерывной в точке x0 ,если существует предел функции в этой точке и он равен значению функции в этой точке.

| Точки разрыва функции | |||||||||||||
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв
|
Дата добавления: 2015-04-18; просмотров: 351; Мы поможем в написании вашей работы!; Нарушение авторских прав |