Метод наименьших квадратов (МНК). Свойства оценок МНК (формулировка теоремы Гаусса-Маркова).

Если некоторая физическая величина зависит от другой величины , то эту зависимость можно исследовать, измеряя y при различных значениях x . В результате измерений получается ряд значений:

x₁, x₂, ..., x_i, , ... , x_n;

y₁, y₂, ..., y_i, , ... , y_n.

По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет метод наименьших квадратов. Экспериментальные точки, как правило, не ложатся точно на кривую. Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой, т.е. [y_i – ƒ(x_i)]² была наименьшей.

На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда

y = kx или y = a + bx.

Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию. Например, если предполагают, что показатель преломления стекла n связан с длиной λ световой волны соотношением n = a + b/λ², то на графике строят зависимость n от λ^-2.

Рассмотрим зависимость y = kx(прямая, проходящая через начало координат). Составим величину φ – сумму квадратов отклонений наших точек от прямой

.

Величина φ всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ имеет минимум

или
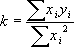(19)

Вычисление показывает, что среднеквадратичная ошибка определения величины k равна при этом

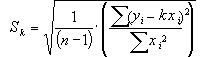, (20)
где – n число измерений.

Рассмотрим теперь несколько более трудный случай, когда точки должны удовлетворить формуле y = a + bx (прямая, не проходящая через начало координат).

Задача состоит в том, чтобы по имеющемуся набору значений x_i, y_i найти наилучшие значения a и b.

Снова составим квадратичную форму φ , равную сумме квадратов отклонений точек x_i, y_i от прямой

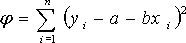
и найдем значения a и b , при которых φ имеет минимум

;

.

.

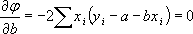Совместное решение этих уравнений дает

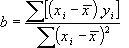(21)

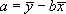. (22)

Среднеквадратичные ошибки определения a и b равны

(23)

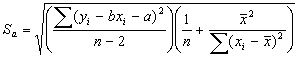. (24)

При обработке результатов измерения этим методом удобно все данные сводить в таблицу, в которой предварительно подсчитываются все суммы, входящие в формулы (19)–(24). Формы этих таблиц приведены в рассматриваемых ниже примерах.

В первую очередь, отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если

математическое ожидание случайных ошибок равно нулю, и

факторы и случайные ошибки — независимые случайные величины.

Первое условие можно считать выполненным всегда для моделей с константой, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).

Второе условие — условие экзогенности факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы 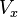к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.

Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:

Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности):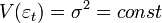

Отсутствие корреляции (автокорреляции) случайных ошибок в разных наблюдениях между собой

Данные предположения можно сформулировать для ковариационной матрицы вектора случайных ошибок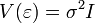

Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными, состоятельными и наиболее эффективными оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbaised Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:

Эффективность означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация коэффициентов, и в частности сами коэффициенты, имеют минимальную дисперсию), то есть в классе линейных несмещенных оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:

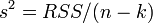
Подставив данное значение в формулу для ковариационной матрицы и получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными и состоятельными. Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.

Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными оценками (оставаясь несмещёнными и состоятельными). Однако, ещё более ухудшается оценка ковариационной матрицы — она становится смещённой и несостоятельной. Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения последней проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта и стандартные ошибки в форме Ньюи-Уеста). Другой подход заключается в применении так называемого обобщённого МНК.

30. Показатели качества регрессии: коэффициент детерминации как мерило качества спецификации эконометрической модели (на примере модели Оукена).

Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.

Для оценки качества модели регрессии используются специальные показатели.

Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:

1) парный линейный коэффициент корреляции, который рассчитывается по формуле:

где G(x) – среднеквадратическое отклонение независимой переменной;

G(y) – среднеквадратическое отклонение зависимой переменной.

Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии 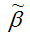по формуле:

Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.

2) коэффициент детерминации рассчитывается как квадрат парного линейного коэффициента корреляции и обозначается как ryx². Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.

Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.

Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:

G²(y)=σ²(y)+δ²(y),

где G²(y) – это общая дисперсия зависимой переменной;

σ²(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:

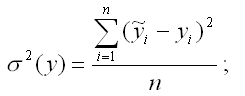
δ²(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:

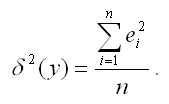
С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:

1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:

Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.

2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:

Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;

3) показатель

характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;

4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE):

где h– это количество параметров, входящих в модель регрессии.

Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений β(у), то модель регрессии можно считать качественной.

Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:

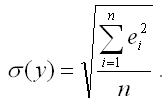
5) показатель средней ошибки аппроксимации рассчитывается по формуле:

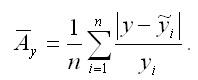
Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.