Система национальных счетов

Разработкой стандартов в области национального счетоводства занимаются международные организации. В настоящее время действующим стандартом является СНС 1993 г., одобренная Статистической комиссией ООН.

Внедрение СНС в статистическую практику — это длительный процесс, который осуществляется поэтапно посредством перехода от БНХ к СНС. Завершающей стадией переходного периода станет организация национального счетоводства, скоординированного с внедрением международных стандартов в бухгалтерский учет.

16. Относительные и средние величины: их виды, значение и практическое применение.

Для обработки экономической информации в анализе хозяйственной деятельности используются следующие методические приемы: относительные и средние величины, группировки, сравнительный анализ, индексные расчеты, балансовый метод, графический, табличный метод, экономико-математические методы.

Рассмотрим каждый из указанных приемов.

Экономические явления, которые изучаются в анализе хозяйственной деятельности, имеют, как правило, количественную определенность, которая выражается в абсолютных и относительных величинах.

Абсолютные величины показывают количественные размеры явления в единицах меры, веса, объема, протяженности, площади, стоимости и т.д. безотносительно к размеру других явлений.

Относительные показатели отражают соотношение величины изучаемого явления с величиной какого-либо другого явления или с величиной этого явления, но взятой за другое время или по другому объекту. Относительные показатели получают в результате деления одной величины на другую. При расчете относительного показателя абсолютный показатель, находящийся в числителе получаемого отношения, называется текущим или сравниваемым. Показатель же, с которым производится сравнение и который находится в знаменателе, называется основанием или базой сравнения. Базой сравнения могут быть данные плана, базисного года, другого предприятия, среднеотрасле­вые и т.д. Относительные величины выражаются в форме коэффициентов (при базе 1), процентов (при базе 100) или промилле (при базе 1000).

Таким образом, рассчитываемый относительный показатель указывает, во сколько раз сравниваемый абсолютный показатель больше базисного, или какую он составляет от него долю, или сколько единиц первого приходится на 1, 100, 1000 и т. д. единиц второго. Проценты, как правило, используются в тех случаях, когда сравниваемый абсолютный показатель превосходит базисный не более чем в 2-3 раза. Проценты же свыше 200-300 обычно заменяются кратным отношением, коэффициентом. Так, вместо 470% говорят, что сравниваемый показатель превосходит базисный в 4,7 раза.

В анализе хозяйственной деятельности используются разные виды относительных величин: планового задания, выполнения плана, динамики, структуры, координации, интенсивности, эффективности.

Все субъекты финансово-хозяйственной сферы, начиная с небольших семейных предприятий и заканчивая крупными концернами, в той или иной степени осуществляют перспективное планирование своей деятельности, а также сравнивают реально достигнутые результаты с ранее намеченными. Для этой цели используются относительные показатели плана (ОП) и выполнения плана (ОВП).

Относительная величина планового задания (ОП) представляет собой отношение планового уровня показателя текущего года к его уровню в прошлом году или к среднему за три-пять предыдущих лет:

Предположим, оборот произведенной продукции коммерческой фирмы в 1996 г. составил
2,0 млрд руб. Исходя из проведенного анализа складывающихся на рынке тенденций, руководство фирмы считает реальным в следующем году довести объем выпуска продукции до 2,8 млрд руб. В этом случае относительный показатель плана, представляющий собой отношение планируемой величины к фактически достигнутой, составит 140% (2,8:2,0∙100%).

Относительная величина выполнения плана (ОВП) - это отношение между фактическим и плановым уровнем показателя, выраженное обычно в процентах:

Предположим, что, исходя из проведенного анализа складывающихся на рынке тенденций, руководство фирмы считало реальным в 1997 г. довести выпуск продукции до 2,8 млрд руб. Фактический выпуск продукции 1997 г. составил 2,6 млрд руб. Тогда относительный показатель выполнения плана, определяемый как отношение фактически достигнутой величины к ранее планировавшейся, составит 92,9% (2,6 : 2,8 · 100%).

Для характеристики изменения показателей за какой-либо промежуток времени используютотносительные величины динамики (ОД) .Их определяют путем деления величины показателя текущего периода на его уровень в предыдущем периоде (месяце, квартале, году). Относительные величины динамики могут бытьбазовыми ицепными. В первом случае каждый следующий уровень динамического ряда сравнивается с базисным годом, а в другом - каждый следующий год относится к предыдущему:

Рассчитанная таким образом величина показывает, во сколько раз текущий уровень превышает предшествующий (базисный) или какую долю от последнего составляет. Если данный показатель выражен кратным отношением, он называется коэффициентом роста, при умножении этого коэффициента на 100% получают темп роста.

Предположим, объем произведенной продукции коммерческой фирмы в 1996 г. составил 2,0 млрд руб., а в 1997 г. - 2,6 млрд руб. Тогда относительный показатель динамики реализации, определяемый как отношение фактически достигнутой в 1997 г. величины к фактически достигнутой в 1996 г., составит 130% (2,6 : 2,0 · 100%).

Между относительными показателями планового задания, выполнения плана и динамики существует следующая взаимосвязь:

ОП · ОВП = ОД.

В нашем примере: 1,40 · 0,929 = 1,3.

Основываясь на этой взаимосвязи, по любым двум известным величинам при необходимости всегда можно определить третью, неизвестную величину.

Показатель структуры (ОС) - это относительная доля (удельный вес) части в общем, выраженная в процентах или коэффициентах:

Относительный показатель структуры выражается в долях единицы или в процентах. Рассчитанные величины (di), соответственно называемые долями, или удельными весами, показывают, какой долей обладает или какой удельный вес имеет i-я часть в общем итоге. Например, удельный вес посевов зерновых культур в общей посевной площади, удельный вес рабочих в общем количестве работников предприятия.

Относительные величины координации (ОК) представляют собой соотношение частей целого между собой, например, активной и пассивной части основных производственных фондов, силовых и рабочих машин и т.д.:

При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической точки зрения. В результате получают, сколько единиц каждой структурной части приходится на 1 единицу (иногда на 100, 1000 и т. д. единиц) базисной структурной части.

Относительными величинами интенсивности (ОИ) называются те, которые характеризуют степень распространенности, развития какого-либо явления в соответствующей присущей ему среде.

Этот показатель исчисляется, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности. Как и в предшествующем случае, он может выражаться в процентах, промилле или быть именованной величиной. Например, степень заболеваемости населения, процент рабочих высшей квалификации и т.д.

Расчет относительных показателей интенсивности в ряде случаев связан с проблемой выбора наиболее обоснованной, соответствующей данному процессу или явлению базы сравнения.

Относительный показатель сравнения (ОСр) представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т. п.):

Например, можно провести сравнение себестоимости однотипных изделий, производимых на двух разных предприятиях. Относительные показатели сравнения дают наглядное представление о соотношении сравниваемых величин и сравнительную оценку объектов, строек, регионов по сравниваемому показателю. Относительные показатели сравнения выражаются в виде отношения (в разах, долях единицы) или в процентах.

Относительные величины эффективности - это соотношение эффекта с ресурсами или затратами, например, производство продукции на 100 га сельскохозяйственной площади, на один рубль затрат, на одного рабочего и т.д.

В практике экономической работы наряду с абсолютными и относитель­ными показателями очень часто применяютсясредние величины. Они используются в анализе хозяйственной деятельности для обобщенной количественной характеристики совокупности однородных явлений по какому-либо признаку в конкретных условиях места и времени. Например, средняя зарплата рабочих используется для обобщающей характеристики уровня оплаты труда изучаемой совокупности рабочих. В средней величине отражаются общие, характерные, типичные черты изучаемых явлений по соответствующему признаку. Она показывает общую меру этого признака в изучаемой совокупности, т.е. одним числом характеризует всю совокупность объектов. С помощью средних величин можно сравнивать разные совокупности объектов, например, районы по уровню урожайности культур, предприятия по уровню оплаты труда и т.д.

Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимыми в анализе явлений и процессов.

Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

Числитель исходного соотношения средней представляет собой ее определяющий показатель. Для средней заработной платы таким определяю­щим показателем является фонд заработной платы. В любом случае независимо от того, какой первичной информацией мы располагаем (известны ли нам общий фонд заработной платы или заработная плата и численность работников, занятых на отдельных должностях, или какие-либо другие исходные данные), среднюю заработную плату можно получить только через данное исходное соотношение средней.

Однако от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины: средняя арифметическая (простая или взвешенная), средняя гармоническая, средняя геометрическая, средняя хронологическая, средняя квадратическая и др.

Все эти способы исчисления средних могут оказаться недостаточными для характеристики типичных черт изучаемой совокупности. Следует иметь в виду, что любая средневзвешенная величина производна от структуры тех данных, которые служат источником расчета.

Выяснение этой стороны дела достигается при помощи структурных средних – моды и медианы. Их принципиальное отличие от средней арифме­тической в том, что они находятся непосредственно по цифровым данным членов ряда. Модой считается та варианта (член числового ряда), которая наиболее часто фигурирует в изучаемом ряду. Она используется в анализе структурных средних как дискретного, так и интервального ряда. В частности, мода может отвечать на вопрос о размере костюма, о марке легковой машины или мотоцикла, которые пользуются наибольшим спросом у потребителя.

Медиана определяется как величина признака у единицы, располо­женной в середине ранжированного ряда. Для практического применения медианы важно знать то ее свойство, что сумма абсолютных величин отклонений от медианы минимальна. При этом имеются в виду линейные отклонения, т.е. абсолютные значения этой величины без учета знаков отклонений (+,–). Указанное свойство медианы имеет существенное значение для практического ее применения, например, при расчетах точки расположения объекта, предназначаемого для обслуживания потребителей определенного района.

При использовании средних величин в анализе хозяйственной деятельности следует учитывать, что они дают обобщенную характеристику явлений, основываясь на массовых данных. В этом их сила и недостаток. Нередко бывает, что за общими средними показателями, которые выглядят довольно неплохо, скрываются результаты плохо работающих бригад, цехов и других хозяйственных подразделений. Поэтому при анализе необходимо раскрывать содержание средних величин, дополняя их среднегрупповыми, а в некоторых случаях и индивидуальными показателями.

17. Корреляционно-регрессионный анализ: сущность, задачи и механизм использования.

Любой - явлении природы и общества не может быть осознанным и понятным без обоснования его связей с другими явлениями Чтобы познать сущность явлений, необходимо раскрыть их взаимоотношения, коли сно определить влияние тех или иных объективных и субъективных факторев.

Влияние этих факторов на уровень экономических показателей в сельском хозяйстве до недавнего времени определялся в основном с помощью метода статистических группировок (этот метод будет рассмотрен в темах за агальнои теории статистики) Соотношение признаков, выявленных в результате статистических группировок, отличаются от соотношений, которые имеют место при функциональных связях, когда каждому значению арг умента соответствует определенное значение функции Метод статистических группировок позволяет установить только наличие связи между явлениями, не определяя при этом его сравнительные количественные параметры Через ц е наряду с методом группам, которые играют важную роль в экономических исследованиях, для решения подобных вопросов необходимо применять и другие методы, в частности, метод корреляции Термин \"корел яция \"впервые применил ЖКювье в работе\" Лекции по Сравнительное анатомии \"(1800-1805 pp) Начальные математические построения метода корреляции были даны избрал в 1846 г (\" корреляция \"- от латинского\" cor relation \"отношения, что означает соотношение, соответствие предметов или понятийіввідношення, відповідність предметів або понять).

корреляции называется неполный связь между изучаемыми явлениями Это такая зависимость, когда любой - либо значению одной переменной может соответствовать несколько различных значений другой переменной Она мульт ражаем закон множества причин и последствий и является свободной неполной зависимостьтю.

В исследованиях важно изучать не столько мере корреляции, сколько форму ее и характер изменения одного признака в зависимости от изменения другой Эти задачи решаются методами регрессионного анализа Первые спро оби применения этого метода в экономике были сделаны в конце XIX и в начале XX века) в России - работы ЕЕСлуцького, ААЧупрова, на Западе - работы ВПарето, Гукера и др. та ін.).

Корреляционный анализ является своего рода логическим продолжением (развитием) метода статистических группировок, его углублением Он помогает решить целый ряд новых задач в экономическом анализе расчеты а основе корреляционных моделей повышают степень точности анализа, часто выявляют недостатки предварительного анализа Преимущество этого метода состоит также и в том, что он дает возможность решать за дачи, которые нельзя решить с помощью других методов экономического анализа - как, например, главу влиянию многих факторов, действующих взаимосвязаны и взаимообусловленыено.

Использование метода корреляции и регрессии позволяет решить следующие основные задачи: 1) установить характер и тесноту связи между изучаемыми явлениями, 2) определить и количественно измерить степень влияния в отдельных факторов и их комплекса на уровень изучаемого явления; 3) на основании фактических данных модели зависимости экономических показателей от различных факторов рассчитывать количественные изменения анализованог в явления при прогнозировании показателей и давать объективную оценку деятельности предпри.

Известно, что существует два типа зависимости явлений: функциональный и корреляционный При функциональной связи изменение одного признака или показателя на определенную величину влечет за собой изменения второго признака или показателя ика на четко определенную величину Такого рода зависимость в ее чистом виде встречается в математике, физике, химииії.

При корреляционной зависимости каком - либо значению одной переменной может соответствовать несколько или даже множество разнообразных, т.е. варьирующих значений другой переменной

Главное отличие корреляционной зависимости от функциональной заключается в том, что функциональная связь имеет место в каждом отдельном случае наблюдения, а корреляционный проявляется так же только в в среднем или в целом для всей данной совокупности наблюдений и является неточным в отношении отдельных наблюде.

Корреляционная связь величин состоит в том, что при задании одной из них устанавливается не одно точное значение, а вероятности различных значений другой Таким образом, зависимость проявляется не между сам мими величинами, а между каждой из них и соответствующим математическим ожиданием иногої.

Изучение взаимосвязей корреляционного типа имеет существенное значение особенно при анализе явлений, которые складываются под воздействием большого количества определенных условиях

По своим математическими особенностями корреляционные зависимости могут быть положительными и отрицательными, прямолинейными и криволинейными, простыми и множественными

Когда определяется связь между двумя признаками, корреляция называется простой, если же явление рассматривается как результат воздействия нескольких факторов - множественной По форме корреляционная зависимость бывает прямол линейной и криволинейной, по направлению-прямой (положительной) и обратной (отрицательной).

Необходимо подчеркнуть две особенности, присущие корреляционном анализа:

1) при использовании корреляционного метода решающее значение имеет всестороннее, экономически осознанный предварительный анализ данных хозяйственной деятельности Следует помнить, что связь между признаками и свойств стями не является результатом математических расчетов, а лежит в природе самих экономических явлений и с помощью методов математической статистики можно лишь выразить объективно существующие закономерности экономической них процессов;

2) корреляцию можно обнаружить, лишь исследуя достаточно большую совокупность наблюдений, поскольку корреляционные связи проявляются в форме сопряженного варьирования двух или нескольких сопоставленных признаков

Корреляционно - регрессионный анализ включает три этапа: 1) математико - экономическое моделирование, 2) решение принятой модели путем нахождения параметров корреляционного уравнения (корреляционное уравнение, за а первичной предложению английского статистика - математика Ф Гальтона, называют также уравнением регрессии), 3) оценка и анализ полученных результатев.

Статистическое исследование корреляционной зависимости включает задачи определения формы связи и нахождения количественной характеристики этой формы Процесс установки формы связи и выбора математического ре ивняння, которое могло бы наиболее полно отражать характер взаимосвязи между признаками изучаемого явления, имеет решающее значение в корреляционном анализі.

Вопрос выбора формы связи и математического уравнения можно решить на основе количественного социально - экономического анализа изучаемых явлений, используя при этом такие методы статистического ана Ализе, как графический, статистические группировки, дисперсионный анализ и др..

При прямолинейном связи увеличение факторного признака (х) вызывает несомненное увеличение (или уменьшение) результативного признака (у) в среднем на определенную величину

Полную характеристику линейной связи можно получить, пользуясь критерием линейной корреляционной зависимости акад ВСНемчинова³ Этот критерий представляет такую ??схему:

1)у^х = у -^х = полное отсутствие линейной корреляционной связи;

2)у^{х у} у o^х - прямая связь между признаками;

3)у^х у -^х - обратная связь между признаками;

4) ух - у - х = ау-ах - _полная линейная функциональная зависимость

В случае, когда в корреляционном анализе используют групповые средние, характер связи между признаками определяют по изменению последних Более или менее правильная систематическое изменение их от группы к группе сви идчить о наличии прямолинейной зависимостиі.

Показателем тесноты связи является линейный коэффициент корреляции, величина которого определяется по формуле:

Преобразование этой формулы приводит к виду:^{х у} Коэффициент корреляции колеблется в пределах от 0 ± 1

18. Сезонные колебания: сущность, методы анализа, индексы сезонности и х использования для прогнозирования динамических рядов.

Если в анализируемой временной последовательности наблюдаются устойчивые отклонения от тенденции (как в большую, так и в меньшую сторону), то можно предположить наличие в ряду динамики некоторых (одного или нескольких) колебательных процессов. Это особенно заметно, когда изучаемые явления имеют сезонный характер, — возрастание или убывание уровней повторяется регулярно с интервалом в один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т. д.).
Уровень сезонности оценивается с помощью:

1) индексов сезонности;

2) гармонического анализа.

Индексы сезонности показывают, во сколько раз факти­ческий уровень ряда в момент или интервал времени t больше среднего уровня либо уровня, вычисляемого по уравнению тенденции f(t). При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов каждого года. Индексы сезонности — это, по существу, относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции. Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.

Сезонными колебаниями называют внутригодичные, постоянно повторяющиеся изменения изучаемых явлений. При анализе рядов внутригодовой динамики получают количественные характеристики, отражающие характер изменения показателей по месяцам годового цикла.
Сезонные колебания описывают индексами сезонности, которые рассчитываются как отношение фактического значения показателя к некоторому теоретическому (расчетному) уровню

Где i - порядковый номер сезонного цикла (года), j - порядковый номер внутрисезонного периода (месяца)

Полученые значения подвержены случайным отклонениям, поэтому производится усреднение по годам и получение средних индексов сезонности для каждого периода годового цикла (месяца)

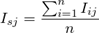
В зависимости от характера изменений ряда динамики формула может рассчитываться разными методами.
Я рассмотрю самый простой метод - метод постоянной средней. Метод может применяться для рядов динамики, где отсутствуют какие-либо тенденции повышения/понижения, либо же они незначительны. Иными словами, наблюдаемая величина колеблется около какого-то постоянного значения.
Здесь

,где , средняя по каждому внутрисезонному периоду j (месяцу) для всех n сезонов

, общая средняя по всем сезонам (n) и внутрисезонным периодам (m)

Анализ сезонных колебаний методами второй группы, суть которых заключается в предварительном определении и исключении общей тенденции развития, применяется в тех рядах динамики, уровни явлений которых имеют выраженную тенденцию увеличения (или снижения) на протяжении изучаемого периода.

Прежде чем производить детальный анализ сезонных колебаний, необходимо произвести предварительный анализ явления с целью установления наличия сезонных колебаний, их периодичности и цикличности и для выбора способа детального анализа. Предварительный анализ производится как непосредственно на эмпирических данных ряда динамики, так и с помощью графических изображений их.

При наличии незначительной тенденции увеличения (или снижения) или при ее отсутствии анализ сезонности такого рода явлений можно производить способами первой группы, т.е. без определения и исключения общей тенденции. При наличии выраженной тенденции, что особенно наглядно проявляется при графическом изображении данных, анализ сезонности следует производить способами второй группы. Для этого определяется общая тенденция развития либо методом механического выравнивания, либо методом аналитического выравнивания по уровням какой-либо кривой (которой соответствует форма связи между изменениями времени и уровнями явления), либо по способу скользящей (подвижной) средней (когда затруднительно выбрать уравнение связи или нет возможности решать сложные системы уравнений).

Сезонные колебания видны из отклонений эмпирических данных продажи от теоретических, т.е. из отклонений от общей тенденции. Сезонные колебания, на которых не сказывается влияние общей тенденции, определяется не только из отклонений данных эмпирического ряда к соответствующим показателям выровненного уровня. Процентированием данных эмпирического ряда к показателям выровненного исключается влияние общей тенденции развития на сезонные колебания и одновременно определяется сезонная волна на протяжении всего изучаемого периода.

19. ВВП – итог экономической деятельности всех производственных единиц страны за определенный период времени. Методы исчисления ВВП. Оценка ВВП в постоянных ценах. Международные сопоставления ВВП.

Валовой внутренний продукт (ВВП) - это один из важнейших показателей системы национальных счетов, который характеризует конечный результат производственной деятельности экономических единиц - резидентов и измеряет стоимость товаров и услуг произведенных этими единицами для конечного использования.

ВВП является показателем произведенного продукта, который представляет собой стоимость произведенных конечных товаров и услуг. Это означает, что стоимость промежуточных товаров и услуг, использованных в процессе производства (таких, как сырье, материалы, топливо. энергия, семена, корма, услуги грузового транспорта, оптовой торговли, коммерческие и финансовые услуги и т. п.), не входит в ВВП. В противном случае, ВВП содержал бы повторный счет.

Кроме того, ВВП - это внутренний продукт, потому что он произведен резидентами.

ВВП - это валовый продукт, потому что он исчисляется вычета потребления основного капитала.

Теоретически внутренний продукт должен определяться на чистой основе, т.е. за вычетом потребления основного капитала. Однако для определения потребления основного капитала в соответствии с принципами системы национальных счетов требуются специальные расчеты на основе данных о восстановительной стоимости основных фондов, сроке их службы и износе по видам основных фондов. Амортизация по данным бухгалтерского учета не подходит для этой цели.