Критерий Дарбина-Уотсона

Ранее мы сказали, что по данным временных рядов могут быть исследованы причинно-следственные связи переменных. Первые два метода исключения тенденции приводят к тому, что вместо исходных уровней ряда мы исследуем зависимость между остатками в рядах динамики, оговариваясь при этом, что остатки не должны содержать тенденции. В противном случае ее присутствие вызвало бы ложную корреляцию.

Однако при моделировании временных рядов встречаются ситуации, когда остатки содержат тенденцию или цикличность (рис.6.1.2). В этом случае остатки не являются независимыми, каждое последующее значение остатка зависит от предыдущего. Это явление получило название автокорреляция остатков.

Назовем причины существования автокорреляции остатков:

1) в модель не включен фактор, оказывающий существенной воздействие на результат; его влияние будет отражаться в остатках, то есть они могут быть автокоррелированы;

2) модель не учитывает влияние нескольких второстепенных факторов, совместное влияние которых может быть существенным (если их тенденции совпадают или фазы цикличности совпадают);

3) автокорреляция остатков может заключаться в неверной функциональной спецификации модели.

Существуют два способа определения автокорреляции в остатках. Первый заключается в визуальном анализе графика зависимостей остатков от времени (см. рис. 6.1.2). Второй способ предполагает использование критерия Дарбина-Уотсона. Величину критерия (d) можно определить по одной из формул

(6.1.4)

либо d 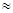2(1 – r_e¹) (6.1.5.),

где r_e¹ – коэффициент автокорреляции остатков первого порядка.

Если в остатках существует полная положительная автокорреляция, то r_e¹=1 и d = 0. Если в остатках полная отрицательная автокорреляция, то

r_e¹=-1 и d = 4. Если автокорреляция остатков отсутствует, то r_e¹=0 и d = 2.

На практике используется следующий алгоритм проверки гипотезы об автокорреляции остатков:

1. выдвигается нулевая гипотеза об отсутствии автокорреляции в остатках;

2. определяется фактическое значение критерия Дарбина – Уотсона (d);

3. по специальным таблицам (приложение учебника по эконометрике) находят критические значения критерия d_L и d_u , где п –число наблюдений, k- независимых переменных в модели, - уровень значимости;

4. числовой промежуток всех возможных значений d разбивается на 5 отрезков

0 d _L d _u 2 4- d _u 4 - d _L 4

5. если d - фактическое попадает в зону неопределенности, то предполагают существование автокорреляции в остатках.

В последнем случае исследовать причинно-следственные связи переменных по остаткам нельзя, получим ложную корреляцию.

Моделирование временных рядов имеет определенную специфику. При развитии любого процесса, в том числе экономического, каждый уровень развития всегда в какой-то мере зависит от уровней того же процесса за предыдущие периоды или моменты времени. Исследование автокорреляции уровней позволяет определить основные группы факторов, формирующих этот процесс. Анализ автокорреляции в остатках позволяет выявить ложную корреляцию и дает возможность изучения истинных связей переменных в рядах динамики