Потеря напора по длине при турбулентному установившемся равномерном движении жидкости. Формула Вейсбаха-Дарси.

Как было указано в п.4.1, для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис.4.4. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υ оср, которое данном случае остается постоянным.

Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.4.5). 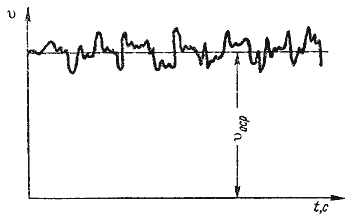Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:

Исследования И. Никурадзе. Общие вопросы о потерях напора.

первые наиболее исчерпывающей работы по определению были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg(1000λ) от lg Re для ряда значений Δ/r 0. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рис. 4.7, где построены кривые зависимости lg (1000λ) от lg Re для ряда значений Δ/r0.

Прямая I соответствует ламинарному режиму движения жидкости.

Далее на графике можно рассматривать три области.

Первая область - область малых Re и Δ/r0, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рис.4.7 прямой II ). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(d / Δ э) коэффициент λ определяется по полуэмпирической формуле Блазиуса

Для определения существует также эмпирическая формула П.К. Конакова, которая применима для гидравлически гладких трубВо второй области, расположенной между линий II и пунктирной линией справа, коэффициент λ зависит одновременно от двух параметров - числа Re и относительной шероховатости Δ/r0, которую можно заменить на Δэ. Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:

Характерные значения Δэ (в мм) для труб из различных материалов приведены ниже: Стекло 0

Трубы, тянутые из латуни, свинца, меди 0…0,002

Высококачественные бесшовные стальные трубы 0,06…0,2

Стальные трубы 0,1…0,5

Чугунные асфальтированные трубы 0,1…0,2

Чугунные трубы 0,2…1,0

Третья область - область больших Re и Δ/r0, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.

Определение λ для этой области производят по упрощенной формуле Альтшуля: