Контрольные задачи

Задача № 1

Объем бочки равен 20 литров. Необходимо определить массу жидко-сти, находящейся в бочке, если ее плотность ρ = 998 кг/м³.

Задача № 2

Найти объем сосуда, заполненного жидкостью, если вес жидкости G = 18 Н, а ее плотность ρ = 995 кг/м³.

Задача № 3

Необходимо определить удельный вес керосина, а также его массу, ес-ли плотность керосина ρ = 800 кг/м³, а объем емкости, в которой перевозят керосин V = 100 л.

Задача № 4

Коэффициент кинематической вязкости нефти ν = 0,4·10^-4 м²/с, а удель-ный вес ее γ = 8800 Н/м³. Определить динамическую вязкость нефти.

Задача № 5

В закрытом сосуде с водой давление на свободной поверхности p₀ = 12 кПа. Точка В заглублена под уровень на h = 0,5 м. Определите абсолютное давление p_аб, действующее на т.В.

Задача № 6

Определить значение внешнего поверхностного давления в закрытом сосуде, если горизонт воды в открытом пьезометре, приключенном к сосуду, возвышается над горизонтом воды в сосуде на 300 см.

Задача № 8

В закрытом сосуде с водой давление на свободной поверхности p₀ = 13 кПа. Определить, на какую высоту отличается горизонт воды в сосуде от го-ризонта воды в пьезометрической трубке, присоединенной к данному сосуду (ρ_в = 1000 кг/м³).

Задача № 9

Поверхностное давление в закрытом сосуде p₀ =2·10⁵ Па. Горизонт воды в открытом пьезометре, присоединенном к сосуду, возвышается на высоту h₁ = 2·L м, а высота от поверхности воды в сосуде до места присоединения пьезометра h₂ = L м. Определить величину L, если плотность воды ρ = 1000 кг/м³.

Задача № 11

В U-образном манометре с водяным заполнением внутренние диаметры трубок соответственно равны 8 и 8,3 мм. При измерении давления уровень в первой трубке переместился на 204 мм. Определить давление, которое показывает манометр.

Задача № 12

Определить показания пружинного манометра, установленного на глубине h = 3 м от поверхности в закрытом резервуаре с бензином, плотность которого ρ = 720 кг/ м³, давление на поверхности p₀ = 24,5∙10⁴ Па.

Задача № 13

Определить давление пара в цилиндре поршневого парового насоса (рис.3, золотниковая коробка, обеспечивающая возвратно-поступательное движение поршня в паровом цилиндре, не показана), необходимое для пода-чи воды на высоту H = 58 м. Диаметры цилиндров: d₁ = 0,3 м; d₂ = 0,18 м (в соответствии с законом Паскаля гидростатическое давление в корпусе насоса p₂ = p₁ω₁ /ω₂).

Задача № 14

Для заливки центробежного насоса 1 установлен вакуум-насос 2 (рис. 4). Какой необходимо создать вакуум, если верх корпуса центробежного насоса находится над уровнем воды в резервуаре на расстоянии H = 3,5 м.

Задача № 15

Две емкости соединены трубопроводом, на котором установлена зад-вижка диаметром d = 0,1 м. Температура воды в правой емкости t_п = 50 ⁰С (ρ_п = 988,07 кг/м³), а в левой - t_л = 20 ⁰С (ρ_л = 998,23 кг/м³). Найти разность сил давления на закрытую задвижку. Высота воды в емкостях h = 2 м (рис. 5).

Задача № 16

Определить силу давления воды на крышку лаза для осмотра в котле системы водяного отопления (диаметр лаза d = 0,8м), если уровень воды в расширительном сосуде находится на высоте Н = 20 м, а центр тяжести крышки на высоте h = 4 м (рис. 6).

Задача № 17

Определить силу суммарного давления воды на плоский щит, перекры-вающий канал, ширина канала b = 1,8 м, глубина воды в нем h = 2,2 м. Построить эпюру избыточного гидростатического давления.

Задача № 18

Определить глубину бассейна, заполненного морской водой с плот-ностью ρ = 1019,37 кг/м³, если на боковую вертикальную стенку со стороны воды действует сила, равная 5000 кН.Длина стенки по горизонтали равна 4 м.

Задача № 19

Для промывки начальных участков канализационной сети построен промывной колодец. Его опорожнение производится с помощью клапана. Определить силу суммарного давления воды на клапан, если глубина воды в колодце H = 1,8 м, диаметр отводной трубы d = 200 мм, а ее центр возвы-шается над дном колодца на высоте h = 150 мм (рис. 7).

Задача № 20

Щит, перекрывающий канал, расположен под углом 45 ⁰ к горизонту и закреплен к опоре над водой. Определить силу суммарного давления воды на щит. Ширина щита b = 2 м, глубина воды перед щитом h₁ = 2,5 м, после щита h₂ = 1,5 м. Опора расположена над уровнем воды на высоте h₃ = 1 м (рис.8).

Задача № 21

Определить вес груза, установленного на круглом в плане металли-ческом понтоне диаметром d = 4 м, если после установки груза осадка пон-тона увеличилась на 0,6 м.

Задача № 22

Простейший ареометр (прибор для определения плотностей жидкос-тей), выполненный из круглого карандаша d = 8 мм и прикрепленного к его основанию металлического шарика диаметром d_ш = 5 мм, имеет вес G = 0,006 Н. Определить плотность жидкости, если ареометр цилиндрической частью погружается в нее на глубину h = 1,5 см.

Задача № 23

Деревянная баржа имеет вертикальные борта и площадь дна ω = 60 м². Вес самой баржи G = 35 кН. Найти ответ на вопрос: а) сможет ли пройти бар-жа в порожнем состоянии; б) сможет ли пройти баржа с грузом гравия

объемом V = 25 м³; при условии, что наименьшая глубина по фарватеру h_min = 1,42 м.

Задача № 24

Объем части ледяной горы, возвышающейся над поверхностью моря V = 12,5 м³. Определить общий объем ледяной горы и глубину ее погруженной части, если в плане она имеет форму прямоугольника размером а ´ b = 3 ´ 2 м, если плотность льда ρ_л = 920 кг/м³, а плотность морской воды ρ_м.в. = 1030 кг/м³.

Задача № 25

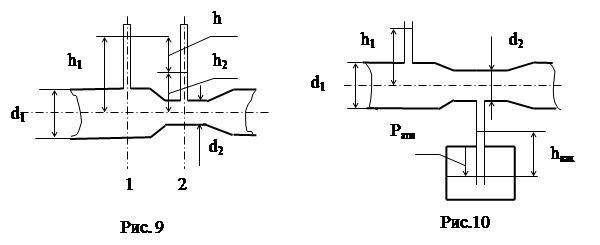
Определить расход воды Q в трубе диаметром d₁ = 250 мм, имеющей плавное сужение до диаметра d₂ = 125 мм (рис. 9), если показания

пьезометров: до сужения h₁ = 50 см; в сужении h₂ = 30 см. Потерями напора пренебречь.

Задача № 26

Требуется определить диаметр суженной части трубы d₂ (рис. 9), если h₁ = 1,0 м, d₁ = 0,1м, а расход жидкости в трубе Q = 9 л/с. Потерями напора пренебречь.

Задача № 27

Определить скорость υ₁ (рис. 9), если h = 2,0 м, диаметр трубы d₁ = 0,1 м, а d₂ = 0,05 м.

Задача № 28

Определить повышение давления Δр при прохождении потока через конический диффузор с диаметром входа и выхода соответственно d₁ = 25 мм и d₂ = 50 мм. Расход жидкости Q = 3 л/с, плотность принять за 1000 кг/м³.

Задача № 29

Определить расход воды Q по показанию водомера Вентури, если h = 55 см, а диаметры в местах установки пьезометров d₁ = 40 мм, d₂ = 15 мм. Потерями напора пренебречь (рис. 9).

Задача № 30

Определить, на какую высоту поднимается вода в трубке, один конец которой присоединен к суженному сечению трубопровода, а другой конец опущен в воду. Расход воды в трубе Q = 0,025 м³/с, избыточное давление p₁ = 49·10³ Па, диаметры d₁ = 100 мм и d₂ = 50 мм (рис. 10).

Задача № 31

Определить полный напор жидкости с расходом Q₁ = 3 л/с, протекаю-щей по расширенному участку трубы, если d₁ = 25 мм и d₂ = 50 мм. Показание пьезометров в сечениях: h₁ = 0,8 м, h₂ = 1,5 м. Потерями напора пренебречь.

Задача № 32

По трубопроводу диаметром d = 20 мм подается масло в количестве Q = 3,14 л/с, коэффициент кинематической вязкости ν = 4 см²/с. Определить режим движения масла.

Задача № 33

Определить режим движения машинного масла, подаваемого для смазки подшипников по трубопроводу диаметром d = 20 мм в количестве Q = 0,628 л/с. Коэффициент кинематической вязкости ν = 1 см²/с.

Задача № 34

В поверхностном подогревателе суммарный расход воды Q = 10 л/с проходит по 250 параллельным трубкам. Каким должен быть диаметр трубок, чтобы обеспечить турбулентный режим движения воды? Коэффициент кинематической вязкости воды ν = 0,013 см²/с.

Задача № 35

В конденсаторе паровой турбины охлаждающая вода с расходом

Q = 25 л/с проходит по 500 параллельным трубкам. Каков допустимый диаметр трубок, при котором в них еще будет турбулентное движение? Коэффициент кинематической вязкости воды ν = 0,01 см²/с.

Задача № 36

Для потока турбинного масла, подаваемого по трубе квадратного сечения со стороной а = 20 мм, определить критическую скорость течения, приняв за определяющий размер потока сторону квадрата и критическое число Рейнольдса как для круглой трубы. Вязкость масла ν = 1 см²/с.

Задача № 37

Трубопровод диаметром d = 0,1 м пропускает машинное масло в коли-честве Q = 50 л/с. Найти минимальное значение коэффициента кинематичес-кой вязкости, при котором в трубопроводе сохранится ламинарный режим.

Задача № 38

Определить минимальный расход воздуха, при котором в трубе диа-метром d = 0,2 м сохраняется турбулентный режим. Плотность воздуха ρ = 1,2 кг/м³, коэффициент динамической вязкости μ = 18·10^-6 Па·с.

Задача № 39

По трубе диаметром d = 4 см подается вода с коэффициентом кинема-тической вязкости ν = 0,01 см²/с. Расход воды Q = 31,4 л/с. Установить режим движения и определить, при каком расходе воды произойдет смена режима.

Задача № 40

Определить критическую скорость движения воды по трубе диамет-ром d = 10^-2 м при температуре воды 20 ⁰С.

Задача № 41

Конденсатор паровой турбины, установленный на тепловой электро-станции, оборудован 8186 охлаждающими трубками диаметром d = 0,025 м. В нормальных условиях работы через конденсатор пропускается циркуляци-онная вода с расходом Q = 3,78 м³/с и температурой воды 13 ⁰С. Будет ли движение воды по трубкам турбулентным?

Задача № 42

Каково соотношение между численными значениями Re_кр для потоков воды и машинного масла, взятых при одинаковой температуре 60 ⁰С? Коэф-фициент кинематической вязкости ν _воды = 0,005 см²/с, ν_масла= 1 см²/с.

Задача № 43

На трубопроводе длиной 1000 м и диаметром d = 200 мм установлены две задвижки (для каждой ξ₁ = 2), дроссельная шайба (ξ₂ = 25), обратный клапан (ξ₃ = 8) и три поворота (для каждого ξ₄ = 1). Определить суммарные потери напора в трубопроводе при скорости υ = 1 м/с и коэффициенте жидкостного трения λ = 0,02.

Задача № 44

При внезапном расширении потока от d₁ и до d₂ = 2d₁ коэффициент местного сопротивления для расчета потерь напора по скорости перед рас-ширением равен ξ₁. Чему равен коэффициент ξ₂ для расчета потерь по ско-рости за расширением?

Задача № 45

В качестве нагревательных приборов системы отопления использованы стальные трубы d₁ = 0,1 м. Стояк, подводящий нагретую воду, и соедини-тельные линии выполнены из труб d₂ = 0,025 м и приварены к торцам нагревательных труб. Определить потери напора при внезапном расширении трубопроводов, если скорость движения горячей воды в подводящих линиях υ = 0,3 м/с.

Задача № 46

На трубопроводе длиной L = 2000 м и диаметром d = 400 м уста-новлено несколько местных сопротивлений с общим коэффициентом Σξ = 20. Найти приведенную длину трубопровода, если коэффициент жидкостного трения λ = 0,02.

Задача № 47

Горизонтальная труба диаметром d₁ = 0,1 м внезапно переходит в трубу диаметром d₂ = 0,15 м. Расход воды в трубе составляет Q = 0,03 м³/с. Определить потери напора при внезапном расширении трубы.

Задача № 48

Определить эквивалентную длину местного сопротивления с коэффи-циентом ξ = 4, установленного на трубопроводе диаметром d = 100 мм. Коэффициент жидкостного трения λ = 0,02.

Задача № 49

Расход воды в трубопроводе длиной L = 5 м и диаметром d = 0,0125 м составляет Q = 0,1 м³/ч. На трубопроводе имеются следующие местные соп-ротивления: поворот (ξ = 1,4), кран (ξ = 0,4). Определить приведенную длину трубопровода.

Задача № 50

Задвижка с коэффициентом местного сопротивления ξ₁ = 0,5 имеет эк-вивалентную длину L_э1 = 5 м. Определить эквивалентную длину местного со-противления, установленного на том же трубопроводе и имеющего коэф-фициент местного сопротивления ξ₂ = 8.

Задача № 51

Определить коэффициент местного сопротивления, установленного на конце трубы диаметром d = 100 мм, если показания пьезометра перед ним H = 1,5 м, а расход жидкости Q = 0,03 м³/с.

Задача № 52

Найти потерю напора на трение при движении воды в стальной новой трубе с внутренним диаметром d = 0,05 м при расходе жидкости Q = 1,96 л/с и температуре 20 ⁰С. Длина трубы L = 1000 м. Значение эквива-лентной шероховатости для стальных труб k_э = 0,06 мм.

Задача № 53

Вентиляционная труба имеет диаметр d = 0,1 м. Определить коэф-фициент λ, если расход воздуха, подаваемый по трубе Q = 0,078 м³/с. Мест-ных сопротивлений по пути не имеется. Коэффициент кинематической вяз-кости ν = 15,7·10^-6 м²/с, эквивалентная шероховатость k_э = 0,2 мм.

Задача № 54

В горизонтальной трубе диаметром d = 0,075 м и длиной L = 300 м расход воды составил Q = 0,0075 м³/с. Температура воды в трубе 10 ⁰С. Коэф-фициент шероховатости k_э = 0,15 мм. Найти потери напора на трение.

Задача № 55

Определить коэффициент жидкостного трения λ для жидкости с рас-ходом Q = 10 л/с в трубе диаметром d = 20 мм, если разность уровней жид-кости в пьезометрах, установленных на расстоянии L = 3 м один от другого, равна h = 0,5 м.

Задача № 56

Найти численное соотношение потерь напора на трение h_тр1/h_тр2 для двух потоков в зоне вполне шероховатого течения, если d₁ = 2d₂, k₁ = k₂,

υ₁ = υ₂.

Задача № 57

Найти численное соотношение потерь напора на трение h_тр1/ h_тр2 для

двух потоков в зоне гидравлически гладкого течения, если d₁ = 2d₂, k₁ = k₂, υ₁ = υ₂.

Задача № 58

Вода с вязкостью ν = 0,01 см²/с движется по трубе диаметром

d = 200 мм со скоростью υ = 0,1 м/с. Абсолютная шероховатость трубы k = 0,5 мм. Определить коэффициент жидкостного трения.

Задача № 59

Определить коэффициент жидкостного трения λ при течении масла с вязкостью ν = 1 см²/с в трубе диаметром d = 100 мм. Скорость движе-ния масла υ = 0,1 м/с, абсолютная шероховатость трубы k = 0,2 мм.

Задача № 60

Нефть с вязкостью ν = 20 см²/с движется по трубе диаметром d = 100 мм и длиной L = 400 м со скоростью υ = 0,2 м/с. Определить расход и потерю напора на трение.

Задача № 61

Найти численное соотношение потерь напора на трение h_тр1/h_тр2 для двух потоков в зоне ламинарного течения, если d₁ = 2d₂, k₁ = k₂, υ₁ = υ₂.

Задача № 62

Определить расход воды Q через сопло диаметром d = 10 мм, при котором теоретическая сила взаимодействия струи с лопастью (α = 60 ⁰) составит P_т =100 H. Скорость струи на уровне лопасти составляет 1 м/с. Сжатием струи на выходе из сопла пренебречь.

Задача № 63

Определить теоретическую силу взаимодействия водяной струи с неподвижной плоской лопастью, если скорость струи υ = 2 м/с, диаметр

выходного сопла d = 20 мм.

Задача № 64

Определить теоретическую силу взаимодействия струи с неподвижным симметричным ковшом гидротурбины (α = 180 ⁰), если скорость струи

υ = 2 м/с, диаметр струи d = 50 мм. Сжатием струи на выходе из сопла пре-небречь.

Задача № 65

Определить скорость струи на выходе из сопла, если расход жидкости Q = 5 л/с, а диаметр сопла d = 20 мм? Коэффициент сжатия струи на выходе из сопла принять за единицу.

Задача № 66

Определить скорость струи на уровне лопасти (α = 60 ⁰), если теоре-тическая сила взаимодействия струи составит P = 200 H. Расход жидкостиQ = 300 л/с.

Задача № 67

Определить отношение теоретических сил взаимодействия струи

P₁/P₂ для конической и плоской лопастей, если ρ₁ = ρ₂, Q₁ = Q₂, υ₁ = υ₂? Скорость на уровне плоской лопасти υ = 4 м/с, скорость струи υ_с = 10 м/с. Определить высоту лопасти над срезом сопла.

Задача № 68

Определить избыточное давление на поверхности жидкости р, при котором будет обеспечен расход воды Q = 100 л/с через цилиндрический на-садок диаметром d = 0,1 м, расположенный на глубине Н = 2 м под уровнем воды. Коэффициент расхода насадка μ = 0,82.

Задача № 69

Определить расход воды, вытекающей из малого отверстия диаметром d = 0,03 м в боковой стенке резервуара больших размеров. Напор над цен-тром отверстия Н = 1м, коэффициент расхода μ = 0,59, коэффициент ско-рости φ = 0,98.

Задача № 70

Из отверстия в тонкой стенке диаметром d = 0,005 м вытекает вода. Оп- ределить расход воды, вытекающей из отверстия. Высота уровня жидкости над центром отверстия Н = 0,05 м, коэффициент расхода μ = 0,66.

Задача № 71

Для двухструйного фонтана использованы отверстие и цилиндричес-кий насадок. Какая струя поднимается выше и во сколько раз? Коэффициент сопротивления отверстия ξ₀ = 0,06, насадка ξ_н = 0,5. Сопротивлением воздуха пренебречь.

Задача № 72

Определить диаметр водоспуска плотины d, обеспечивающий расход воды Q = 6,28 м³/с при разности уровней воды в бьефах Н = 5,1м. Коэффици-ент сопротивления водоспуска, работающего как насадок ξ = 0,56.

Задача № 73

Определить скорость струи υ и расход Q при истечении воды через коноидальный насадок диаметром d = 200 мм при напоре Н = 2,5 м. Коэф-фициент сопротивления насадка ξ = 0,064.

Задача № 74

Определить расход при истечении через внешний цилиндрический на-садок диаметром d = 100 мм при напоре Н = 6 м. Коэффициент скорости

φ= 0,82.

Задача № 75

Определить расход Q и коэффициент расхода μ при истечении через отверстие диаметром d = 100 мм, если скорость струи υ = 5,81 м/с, ее диаметр d_с = 80 мм, коэффициент скорости φ = 0,97.

Задача № 76

При каком напоре Н будет обеспечен расход Q = 35 л/с при истечении через конически расходящийся насадок с диаметром выходного сечения

d = 100 мм. Коэффициент скорости φ = 0,45.

Задача № 77

Требуется определить напор Н, необходимый для пропуска воды в

количестве Q = 25 л/с по трубопроводу длиной L = 1000 м и диаметром

d = 400 мм. Шероховатость стенкок трубы k = 0,1 мм, температура воды

t = 20 ⁰С. По пути имеются местные сопротивления ∑ξ = 50.

Задача № 78

Требуется определить пропускную способность трубопровода, если напор в системе Н = 10 м, длина трубы L = 400 м и диаметр трубы d = 200 мм. Шероховатость стенок трубы k = 0,3 мм, коэффициент кинематической вязко-сти ν = 1,2 10^-6 м²/с. Местными потерями напора пренебречь.

Задача № 79

Необходимо определить диаметр трубопровода d, если расход Q = 15 л/с, длина трубопровода L = 300 м и напор Н = 10 м. Шероховатость трубы

k = 1 мм, коэффициент кинематической вязкости ν = 1,2∙10^-6 м²/с. Суммарные потери напора составляют 15 м.

Задача № 80

Найти потери давления на трение при движении воздуха в бетонной трубе диаметром d = 1 м при давлении, близком к атмосферному, и темпера-туре t = 20 ⁰С. Расход воздуха при заданных условиях Q = 15,6 м³/с, коэф-фициент кинематической вязкости ν = 15,7∙10^-6 м²/с и плотность воздуха

ρ = 1,16 кг/м³. Шероховатость трубы k = 0,5 мм.