Относительное равновесие жидкости.

Относительным равновесием жидкости называется такое ее состояние, при котором каждая ее частица сохраняет свое положение относительно твердой стенки движущегося резервуара, в котором находится жидкость (см. рис. 2.21).

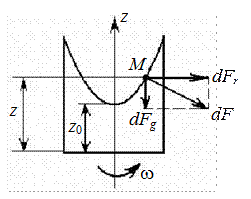
Рис. 2.21. Относительное равновесие жидкости во вращающемся сосуде

При относительном покое рассматриваются две задачи: определяется форма поверхности уровня или равного давления и выясняется характер распределения давления. В данном случае необходимо учитывать силы инерции, дополняющих систему массовых сил, действующих в покоящейся жидкости.

Рассмотрим случай, когда сосуд с жидкостью вращается вокруг своей оси с постоянной скоростью. Для определения формы свободной поверхности и закона распределения давления выберем вблизи свободной поверхности частицу жидкости массой dm. На эту частицу действует массовая сила dF, направленная по нормали к поверхности. Разложим эту силу на две составляющие: горизонтальную 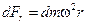и вертикальную .

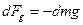Разделив действующие силы на dm, получим дифференциальное уравнение поверхности уровня

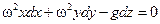или .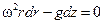

Проинтегрировав, получаем

.

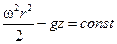(2.20)

Вывод: При вращении резервуара с постоянной скоростью вокруг вертикальной оси поверхностями равного давления будет семейство параболоидов вращения.

Для точки М, находящейся на свободной поверхности жидкости

.

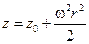Закон распределения давления найдем из дифференциального уравнения гидростатики, которое в данном случае примет вид

.

После интегрирования с учетом граничных условий ( 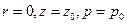), получаем:

.

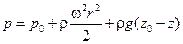Если представить, что

,

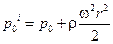то получим уравнение

.

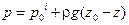(2.21)

Вывод: Распределение давления подчиняется линейному закону для любой фиксированной цилиндрической поверхности.