Основы моделирования. Масштабы.

При изучении гидроаэродинамических явлений необходимо широкое применение эксперимента. Например, все вопросы, касающиеся турбулентного движения жидкости, не имеют точного теоретического решения, поэтому экспериментальные решения дополняют теоретические. Все виды гидравлических сопротивлений и соответствующие им коэффициенты определяются экспериментальным путем.

Перед постановкой исследования экспериментатор должен знать: каким требованиям должна удовлетворять модель, какие величины надо измерять в опытах, какими приборами надо пользоваться, на какие полученные величины, прежде всего, необходимо обращать внимание. Кроме того, необходимо четко знать, что полученные результаты соответствуют явлениям, которые будут иметь место в действительности.

Различают математическое моделирование (на ЭВМ) и физическое (на физических моделях). Физическое моделирование проводят на моделях натурных объектов, которые просты в изготовлении и их размеры позволяют осуществлять в лабораторных условиях эксперименты, задаваясь различными параметрами модели и исследуемого явления, и выявлять искомые закономерности.

Обоснование моделирования и использование в натуре результатов экспериментов на модели связано с подобием движения в натуре и на модели. Подобными называют явления, происходящие в геометрически подобных системах одинаковой физической природы, когда одинаковые величины (например скорости или силы), действующие в подобных точках, имеют между собой постоянные отношения, которые называются масштабами.

Для установления подобия гидроаэродинамических явлений между натурой и моделью следует использовать правила механического подобия. Механическое подобие подразумевает выполнение геометрического, кинематического и динамического подобия.

Геометрически подобными являются два потока, если между их соответствующими линейными размерами существует соотношение

,

(3.1)

где 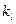– линейный масштаб, показывающий во сколько раз размеры модели изменены по сравнению с размерами натуры; и – геометрические размеры натуры и модели соответственно (длина, ширина или высота).

Производными от линейного масштаба являются масштаб площадей и масштаб объемов .

Кинематическими подобнымиявляются два потока, если поля скоростей на модели и в натуре в подобных точках пространства связаны масштабом

,

(3.2)

соответственно масштаб ускорений можно выразить отношением

.

Для динамического подобиянеобходимо, чтобы все силы одинаковой природы, действующие в подобных точках модели и натуры на частицы жидкости, отличались между собой только постоянными масштабами

.

Любой масштаб может быть выражен через другие масштабы, например, масштаб сил можно представить следующими выражениями

.

Геометрически подобные системы не обязательно будут кинематически и динамически подобными. В то же время динамическое подобие подразумевает автоматически кинематическое и геометрическое подобие.