
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристика приемов введения понятий
Возможны следующие приёмы при введении понятий:
1) можно составить такие упражнения, которые позволяют учащимся быстро сформулировать определение нового понятия.
Например: а) Выписать несколько первых членов последовательности (  ), у которой
), у которой  =2,
=2,  . Такая последовательность называется геометрической прогрессией. Попытайтесь сформулировать её определение. Можно ограничиться подготовкой к восприятию нового понятия.
. Такая последовательность называется геометрической прогрессией. Попытайтесь сформулировать её определение. Можно ограничиться подготовкой к восприятию нового понятия.
б) Выписать несколько первых членов последовательности (  ), у которой
), у которой  =4,
=4,  Далее учитель сообщает, что такая последовательность называется арифметической прогрессией и сам сообщает её определение.
Далее учитель сообщает, что такая последовательность называется арифметической прогрессией и сам сообщает её определение.
2) при изучении геометрических понятий упражнения формулируются таким образом, чтобы учащиеся построили сами необходимую фигуру и смогли выделить признаки нового понятия, необходимые для формулировки определения.
Например: постройте произвольный треугольник, соедините отрезком его вершину с серединой противоположной стороны. Такой отрезок называется медианой. Сформулируйте определение медианы.
Иногда предлагается составить модель либо, рассматривая готовые модели и чертежи, выделить признаки нового понятия и сформулировать его определение.
Например: введено в 10 классе определение параллелепипеда. По предложенным моделям наклонного, прямого и прямоугольного параллелепипедов выделить признаки, по которым эти понятия различаются. Сформулировать соответствующие определения прямого и прямоугольного параллелепипедов.
3) Многие алгебраические понятия вводятся на основании рассмотрения частных примеров.
Например: графиком линейной функции является прямая.
4) Метод целесообразных задач, (разработан С.И. Шохором-Троцким) С помощью специально подобранной задачи учащиеся приходят к выводу о необходимости введения нового понятия и целесообразности придания ему именно такого смысла, который оно уже имеет в математике.
В 5-6 классах таким методом вводятся понятия: уравнение, корень уравнения, решение неравенств, понятие действий сложения, вычитания, умножения, деления над натуральными числами, десятичными и обыкновенными дробями и т.д.
Конкретно-индуктивный метод
Сущность:
а) рассматриваются конкретные примеры;
б) выделяются существенные свойства;
в) формулируется определение;
г) выполняются упражнения: на распознавание; на конструирование;
д) работа над свойствами, не включёнными в определение;
е) применение свойств.
Например: тема – параллелограммы:

|
|

 а)
а)

| |||||

| 
| ||||
1, 3, 5 – параллелограммы.
б) существенные признаки: четырёхугольник, попарная параллельность сторон.
в) распознавание, построение:
г) найти (построить) четвёртую вершину параллелограмма (* - задача №3, ст.96, Геометрия 7-11 класс: Сколько можно построить параллелограммов с вершинами в трёх заданных точках, не лежащих на одной прямой? Постройте их.).
д) другие свойства:
AC и BD пересекаются в точке О и АО=ОС, ВО=ОD; АВ=СD, AD=BC.
е) 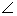 А=
А= 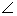 С,
С, 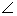 В=
В= 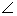 D.
D.


| O |
 B
B
AD
Закрепление: решение задач №4-23, стр.96-97, Геометрия 7-11, Погорелов.
Перспективное значение:
а) используется при изучении и определении прямоугольника и ромба;
б) принцип параллельности и равенства отрезков, заключённых между параллельными прямыми в теореме Фалеса;
в) понятие параллельного переноса (вектора);
г) свойство параллелограмма используется при выводе площади треугольника;
д) параллельность и перпендикулярность в пространстве; параллелепипед; призма.
Абстрактно-дедуктивный метод
Сущность:
а) определение понятия:  - квадратное уравнение;
- квадратное уравнение;
б) выделение существенных свойств: х – переменная; a, b, c – числа; а≠0 при 
в) конкретизация понятия:  - приведенное; примеры уравнений
- приведенное; примеры уравнений 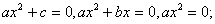
г) упражнения: на распознавание, на конструирование;
д) изучение свойств, не включённых в определение: корни уравнения и их свойства;
е) решение задач.
В школе абстрактно-дедуктивный способ применяется тогда, когда новое понятие полностью подготовлено изучением предыдущих понятий, в том числе изучением ближайшего родового понятия, а видовое отличие нового понятия весьма простое и понятное учащимся.
Например: определение ромба после изучения параллелограмма.
Кроме того, указанный метод используется:
1) при составлении “родословной” определения понятия:
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это параллелограмм, у которого все углы прямые.
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны.
Четырёхугольник – фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.
Иначе говоря, родословная представляет собой цепочку понятий, построенных через обобщения предыдущего понятия, финалом которой является неопределяемое понятие (напомним, что в курсе школьной геометрии к таковым относятся точка, фигура, плоскость, расстояние (лежать между));
2) классификация;
3) применяется к доказательствам теорем и решению задач;
4) широко используется в процессе актуализации знаний.
Рассмотрим этот процесс, представленный системой задач:
а) Дан прямоугольный треугольник со сторонами 3см и 4см. Найти длину медианы, проведённой к гипотенузе.
б) Доказать, что медиана, проведённая из вершины прямого угла треугольника, равна половине гипотенузы.
в) Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, проведёнными к гипотенузе.
г) На продолжении наибольшей стороны АС треугольника АВС отложен отрезок СМ, равный стороне ВС. Доказать, что 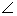 АВМ тупой.
АВМ тупой.
В большинстве случаев в школьном преподавании применяется конкретно-индуктивный способ. В частности, таким методом вводятся понятия в пропедевтических циклах начал алгебры и геометрии в 1-6 классах, причём многие определяющие понятия вводятся описательно, без строгих формулировок.
Незнание учителем различных методов введения определений приводит к формализму, который проявляется следующим образом:
а) учащиеся затрудняются применить определения в непривычной ситуации, хотя и помнят его формулировку.
Например: 1) считают функцию  - чётной, т.к. “cos” – чётная;
- чётной, т.к. “cos” – чётная;
2)  - не понимают связь между монотонностью функции и решением неравенства, т.е. не могут применять соответствующие определения, в которых основной приём исследования состоит в оценке знака разности значений функции, т.е. в решении неравенства.
- не понимают связь между монотонностью функции и решением неравенства, т.е. не могут применять соответствующие определения, в которых основной приём исследования состоит в оценке знака разности значений функции, т.е. в решении неравенства.
б) учащиеся обладают навыками решения задач какого-либо типа, но не могут объяснить, на основании каких определений, аксиом, теорем они выполняют те или иные преобразования.
Например: 1)  - преобразовать согласно этой формуле
- преобразовать согласно этой формуле  и
и 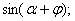 2) представьте, что на столе – модель четырёхугольной пирамиды. Какой многоугольник будет основанием этой пирамиды, если модель положить на стол боковой гранью? (четырёхугольник).
2) представьте, что на столе – модель четырёхугольной пирамиды. Какой многоугольник будет основанием этой пирамиды, если модель положить на стол боковой гранью? (четырёхугольник).
Процесс формирования знаний, умений и навыков не ограничивается сообщением новых знаний.
Эти знания должны быть усвоены и закреплены.
Дата добавления: 2015-04-21; просмотров: 349; Мы поможем в написании вашей работы!; Нарушение авторских прав |