Роль текстовых задач

В обучении математике велика роль текстовых задач.

Решая задачи, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Задачи способствуют развитию их логического мышления. Большое значение имеет решение задач и в воспитании личности учащихся. Поэтому важно, чтобы учитель имел глубокие представления о текстовой задаче, о её структуре, умел решать такие задачи различными способами.

Текстовая задача – есть описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения.

Решение задач – это работа несколько необычная, а именно умственная работа. А чтобы научиться какой-либо работе, нужно предварительно хорошо изучить тот материал, над которым придётся работать, те инструменты, с помощью которых выполняется эта работа.

Значит, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.

Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства. Это означает, что анализ условия задачи необходимо соотносить с вопросом задачи и, наоборот,вопрос задачи анализировать направленно с условием. Их нельзя разрывать, так как они составляют одно целое.

Математическая задача – это связанный лаконический рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии.

Любая текстовая задача состоит из двух частей: условия и требования (вопроса).

В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними.

Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме(«Найти площадь треугольника.» или «Чему равна площадь прямоугольника?»).

Рассмотрим задачу: На тракторе «Кировец» колхозное поле можно вспахать за 10 дней, а на тракторе «Казахстан» – за 15 дней. На вспашку поставлены оба трактора. За сколько дней будет вспахано это поле?

В задаче пять неизвестных значений величин, одно из которых заключено в требовании задачи. Это значение величины называется искомым.

Иногда задачи формируются таким образом, что часть условия или всё условие включено в одно предложение с требованием задачи.

В реальной жизни довольно часто возникают самые разнообразные задачные ситуации. Сформулированные на их основе задачи могут содержать избыточную информацию, то есть, такую, которая не нужна для выполнения требования задачи.

На основе возникающих в жизни задачных ситуаций могут быть сформулированы и задачи, в которых недостаточно информации для выполнения требований. Так в задаче: «Найти длину и ширину участка прямоугольной формы,если известно, что длина больше ширины на 3 метра» – недостаточно данных для ответа на её вопрос. Чтобы выполнить эту задачу, необходимо её дополнить недостающими данными.

Одна и та же задача может рассматриваться как задача с достаточным числом данных в зависимости от имеющихся и решающих значений.

Рассматривая задачу в узком смысле этого понятия, в ней можно выделить следующие составные элементы:

1. Словесное изложение сюжета, в котором явно или в завуалированной форме указана функциональная зависимость между величинами, числовые значения которых входят в задачу.

2. Числовые значения величин или числовые данные, о которых говорится в тексте задачи.

3. Задание, обычно сформулированное в виде вопроса, в котором предлагается узнать неизвестные значения одной или нескольких величин. Эти значения называют искомыми.

Задачи и решение их занимают в обучении школьников весьма существенное место и по времени, и по их влиянию на умственное развитие ребенка.

Понимая роль задачи и её место в обучении и воспитании ученика, учитель должен подходить к подбору задачи и выбору способов решения обоснованно и чётко знать, что должна дать ученику работа при решении данной им задачи.

1. Анализ содержания задачи.

Основная цель ученика на первом этапе— это понять задачу. Ученик должен четко представить себе: о чем эта задача? Что в задаче известно?Что нужно найти?Как связаны между собой данные (числа,величины, значения величин)? Какими отношениями связаны данные и неизвестные,данные и искомое?Что является искомым: число,отношение,некоторое утверждение?

Можно выделить следующие возможные приемы выполнения первого этапа решения текстовой задачи.

1. Представление жизненной ситуации, описанной в задаче, мысленное участие в ней.С этой целью полезно после чтения задачи предложить учащимся представить себе то, о чем говорится в задаче, и предложить нарисовать словесную картинку.

2. Разбиение текста на смысловые части и выделение на этой основе необходимой для поиска решения информации.

Например:«Один человек выпьет кадь пития в 14 дней,а с женою ту же кадь в 10 дней.И ведательно есть, в колико дней жена его особенно выпьет ту же кадь?»

3. Переформулировка текста задачи:замена описания данной в ней ситуации другой,сохраняющей все отношения и зависимости и их количественные характеристики,но более явно их выражающие.

Цель переформулировки— опустить несущественные детали, уточнить и раскрыть смысл существенных элементов.

Рассмотрим на примере простой задачи:«Утром в магазине было 30 книжных шкафов. К концу рабочего дня осталось 12 шкафов.Сколько шкафов продали за день?» — удобнее искать, если текст ее будет сформулирован так: «Было 30 шкафов.Осталось 12 шкафов.Сколько шкафов продали?»

4. Очень важно при работе над задачей научить учащихся выделять основные(опорные) слова,которые связаны с действием,соответствующим сюжету.

2. Поиск пути решения задачи и составление плана ее решения

Цель ученика на втором этапе— выделить величины, данные и искомые числа,входящие в задачу, установить связи между данными и искомым и на этой основе выбрать соответствующее действие.

Использование различных методических приемов при обучении решению текстовых задач способствует развитию кругозора учащихся, правильному пониманию математического смысла различных жизненных ситуаций,активизирует их познавательную активность.На данном этапе используются различные способы моделирования.

1. Предметное моделирование.

Рассматривается,например, задача:«У Лены было6 карандашей,а у Тани 4 карандаша.Сколько карандашей у обеих девочек?»К доске выходят две девочки.У одной из них в руке 6 карандашей,у другой — 4карандаша.Такое воспроизведение уточняет представления детей, возникшие при восприятии ими задачи.

2. Графические модели (это рисунки и чертежи,которые помогают понять задачу,организовать поиск ее решения).

Рисунок может быть таким, что по нему, не выполняя арифметического действия, легко дать ответ на поставленный в задаче вопрос,например: Задача Л. Эйлера1«Крестьянка принесла на рынок некоторое число яиц. Первому покупателю она продала половину того,что имела, и еще пол-яйца;второму – половину того, что у нее осталось, и еще пол-яйца; третьему– половину нового остатка и еще пол-яйца;четвертому– половину того, что осталось,и еще пол-яйца.После этого у нее ничего не осталось.Сколько яиц было у нее вначале?»

Решение:

Что было у крестьянки перед встречей с четвертым покупателем?Что-то, половина чего была продана,после чего осталось пол-яйца.Но, значит, пол-яйца были второй половиной того,что у нее было.Значит, перед встречей с четвертым покупателем у крестьянки было одно яйцо.Нарисуем его в виде одной клетки. Перед встречей с третьим покупателем у нее было это яйцо и те пол-яйца,которые она продала третьему,и все это составляло половину того,что она имела.Значит, пририсуем пол-яйца и удвоим полученное– эти три яйца были у крестьянки перед встречей с третьим покупателем.Аналогично,пририсовав к трем яйцам пол-яйца и удвоив полученное,будем иметь семь яиц, имевшиеся у нее перед встречей со вторым покупателем.Проделав еще раз эту операцию,узнаем, сколько было у нее яиц в самом начале.

текстовый задача математика познавательный

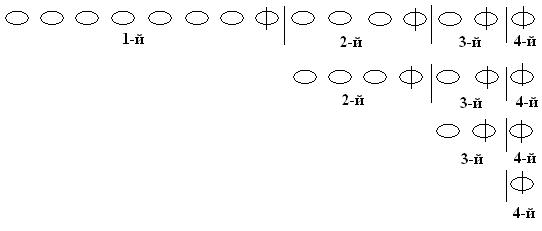
Ответ:15 яиц.

Заметим,что полученный ответ следует проверить: 1-му покупателю продано 15 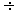2 + 0,5 = 8 яиц, после чего осталось7 яиц, 2-му покупателю продано 7 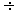2 + 0,5 = 4 яйца, после чего осталось3 яйца, 3-му покупателю продано 3 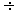2 + 0,5 = 2 яйца, после чего осталось1 яйцо, 4-му покупателю продано 1 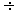2 + 0,5 = 1 яйцо, после чего не осталось ничего.

3. Схематическая модель — это краткая запись задачи (в методической литературе рассматриваются различные виды краткой записи).Например: «Средний из трех братьев старше младшего на два года, а возраст старшего брата превышает сумму лет двух остальных братьев четырьмя годами. Найти возраст каждого брата,

если вместе им 96 лет»

Схематическая запись: Первому брату x –лет, второму2+x, а третьемуx+2+x+4

3. Осуществление плана решения задачи

Выбрав какой-нибудь метод решения,учащиеся переходят к его выполнению,т. е. к третьему этапу решения задачи.

Выполнение плана решения задачи представляется учеником устно или письменно(целиком или фрагментарно).Иногда выполняемые записи или построения сопровождаются устным комментарием.

4. проверка решения задачи

Способов проверки решения задачи много:

Самый элементарный – прикидка ответа (установление границ искомого числа). Прикидка позволяет заметить неправильность рассуждения, несоответствие между величинами, но для многих задач она не применима.

Самый полезный, универсальный – составление и решение обратной задачи. Этот способ проверки развивает мышление, способность рассуждать, но является громоздким и отнимает много времени.

Самый надежный способ проверки – решение задачи другим способом. Во второй главе приведено множество задач, решенных двумя способами.

6. Дополнительная работа над решенной задачей.

Эффективным средством формирования творческой активности и мышления учащихся, дающим возможность более полно реализовать обучающие,развивающие и воспитывающие функции задач,является дополнительная работа над уже решенной задачей:

изменение условия задачи;

постановка нового вопроса;

сравнение содержания данной задачи и ее решения с содержанием и решением другой задачи;

анализ выполненного решения;

обоснование правильности решения;

составление задач по аналогии.

Таким образом, практическая ценность обучения школьников решению текстовых задач разнообразными методами в современных условиях заключается совсем не в том, что это обучение раз и навсегда вооружит их примерами решения различных задач, возникающих на практике и в дальнейшем обучении, а в том, что оно обогатит их опыт мыслительной деятельности.Использование на уроках математики старинных занимательных задач способствует развитию мышления и речи, развитию сообразительности и памяти.