Методика изучения числовых систем. Натуральные числа

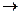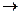Изучение чисел в школьном курсе математики ведется в такой последовательности: натуральные числа, нуль, дроби (положительные), отрицательные чисел и множество рациональных чисел, иррациональные числа и множество действительных чисел. Эта последовательность отражает исторический путь развития понятия числа в математике: N Q₊ Q 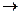R (историческая схема развития понятия числа). В математике дроби возникли значительно раньше, чем отрицательные числа. 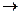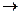В современной математике принята другая последовательность: N Z Q 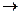R (логическая схема развития понятия числа). От исторической она отличается более ранним введением отрицательных чисел. Поэтому в такой последовательности после натуральных чисел изучаются целые числа. Приверженность школьного курса исторической схеме объясняется тем, что понятие дроби доступнее, чем понятие отрицательного числа.

п.1. Методика изучения натуральных чисел.Множество натуральных чисел изучается с начальной школы. Без понимания структуры множества N нельзя достичь понимания структуры множеств Z, Q, R. Уже в начальных классах учащиеся понимают, что отношение «меньше» устанавливает определенный порядок в множестве N. Это объясняется с помощью упражнения: «b следует за a или a предшествует b, если 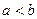». Далее на базе отношения «меньше» разъясняются более сложные отношения: «лежит между» и «непосредственно следует за» - это определяет свойство дискретности (то есть между ними нет ничего).

Правильная ориентация в методике изучения натуральных чисел в 5 классе предполагает знание, с одной стороны, связи данной темы с курсом 1-4 классов, с другой стороны – знание нового в содержании учебного материала и методике его изложения в 5 классе. Необходимо также учитывать общие особенности учебника математики 5 класса. В этом учебнике усиливается роль теоретического материала: приводятся определения, математические термины и обозначения, формулируются факты и законы, отдельные факты получают теоретическое объяснение. В учебниках соответствующий теоретический материал излагается в виде небольших фрагментов, после чего приводятся упражнения и задачи.

В 5 классе даются определения (или описания) понятий: натурального числа, десятичной записи числа, миллиарда, координатного луча, координаты точки, суммы двух чисел, слагаемых, числового выражения, значения выражения, разложения числа по разрядам, разрядных слагаемых, разности двух чисел, уменьшаемого, вычитаемого, произведения двух чисел, множителей, частного двух чисел, делителя числа, кратного числа и др. При этом учителю необходимо различать, в каком случае в учебнике приводится полноценное в логическом отношении определение, а в каком – описание понятия, не претендующее на строгость.

Пример 1. Понятие натурального числа. В учебнике говорится, что «числа, употребляемые при счете предметов, называются натуральными числами». Это описание. В математике при аксиоматическом построении теории натуральных чисел понятие натурального числа является неопределяемым (исходным). В тех случаях, когда понятие вводится описанием, заучивать соответствующую формулировку с учащимися не нужно.

Пример 2. В учебнике говорится: «Вычесть из числа a число b – значит найти такое число х, которое в сумме с числом b дает a: 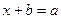. Число х называют разностью чисел a и b, число a - уменьшаемым, а число b – вычитаемым». Это пример настоящего определения, которое именно в таком виде широко используется в математической науке. Наличие определений в 5 классе является одним из признаков повышения теоретического уровня изложения учебного материала. Понятие разности двух чисел должно быть разъяснено, а формулировка определения – тщательно отработана. Таким образом, учителю важно выяснить для себя, какие понятия, относящиеся к натуральным числам, вводятся в учебнике описанием, а какие – определением. Это позволит четче выделить элементы нового подхода в методике изучения натуральных чисел в 5 классе (по сравнению с методикой изучения числового материала в начальных классах). Усиление роли теоретических объяснений проявляется в сочетании индукции и дедукции.