Методика изучения числовых систем. Обыкновенные дроби

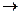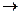Изучение чисел в школьном курсе математики ведется в такой последовательности: натуральные числа, нуль, дроби (положительные), отрицательные чисел и множество рациональных чисел, иррациональные числа и множество действительных чисел. Эта последовательность отражает исторический путь развития понятия числа в математике: N Q₊ Q 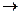R (историческая схема развития понятия числа). В математике дроби возникли значительно раньше, чем отрицательные числа. 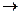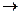В современной математике принята другая последовательность: N Z Q 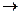R (логическая схема развития понятия числа). От исторической она отличается более ранним введением отрицательных чисел. Поэтому в такой последовательности после натуральных чисел изучаются целые числа. Приверженность школьного курса исторической схеме объясняется тем, что понятие дроби доступнее, чем понятие отрицательного числа.

п.2. Методика изучения обыкновенных и десятичных дробей.Первое знакомство с обыкновенными дробями происходит в 3 классе параллельно изучению натуральных чисел. Систематическое изучение дробей начинается в 5 классе. Десятичные дроби не являются новыми числами по сравнению с обыкновенными дробями. Они представляют лишь другую запись ранее известных обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. В математических вычислениях и практических расчетах более удобными являются десятичные дроби. Обыкновенные дроби в вычислениях используются гораздо реже.

В методике математики существуют различные подходы к порядку изучения обыкновенных и десятичных дробей: 1) вначале изучаются обыкновенные дроби, затем – десятичные (традиционный подход), 2) вначале изучаются десятичные дроби, затем – обыкновенные, 3) смешанный вариант, при котором изучение обыкновенных и десятичных дробей чередуется. В учебнике Виленкина придерживаются смешанного варианта. Вначале в нем вводится понятие обыкновенной дроби. Затем рассматриваются вопросы сравнения, сложения и вычитания дробей с одинаковыми знаменателями. После этого осуществляется переход к десятичным дробям и рассматриваются все четыре арифметических действия над ними. Изучение десятичных дробей начинается и заканчивается в 5 классе. После этого в 6 классе вновь возвращаются к обыкновенным дробям: изучают сравнение произвольных дробей, арифметические действия над ними. Понятие процента примыкает к понятию десятичной дроби. Проценты – это новая форма записи десятичных дробей со знаменателем 100: 1%= =0,01, 15%= =0,15 и т.д..

Центральным в теме «Дробные числа» (5 класс) является понятие обыкновенной дроби. Оно вводится таким описанием (аналогично тому, как это делалось в 3 классе): приводится рисунок с изображением пирога, разрезанного на четыре равные части. Одна из них лежит на одной тарелке, а три части – на другой. Говорят: «На первой тарелке лежит одна четвертая часть пирога, а на второй – три четвертых части пирога». 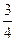Пишут: « пирога, пирога». Далее сообщают, что такие числа как и 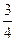, называют обыкновенными дробями. В дроби 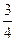число 3 называют числителем дроби, а число 4 – ее знаменателем. Характеристика дроби начинается со знаменателя: знаменатель показывает, на сколько равных частей разрезан пирог, а числитель – сколько надо взять таких частей. Числитель пи шут над чертой, а знаменатель – под чертой. Проведенные разъяснения повторяются на других примерах. Вместо пирога может быть взят круг (отрезок, прямоугольник, квадрат), разделенный на шесть(восемь, семь восемнадцать) равных частей.