Кодирование канала

27. Корректирующим называется код, способный:
1) передавать информацию при использовании минимального количества символов;
2) предотвращать появление ошибок при демодуляции цифрового сигнала;
3) исправлять форму принимаемых импульсов;
4) обнаруживать и (или) исправлять ошибки, возникающие в канале с помехами.

28. Современные корректирующие коды ориентированы на обнаружение (исправление):
1) любых ошибок;
2) ошибок большой кратности;
3) ошибок малой кратности;
4) нетипичных ошибок.

29. Декодирование по минимуму расстояния применяется для:
1) обнаружения и (или) исправления ошибок в кодовой комбинации;
2) определения кодового расстояния применяемого кода;
3) определения расстояния между кодовыми комбинациями применяемого кода;
4) повышения отношения сигнал/шум.

30. Кодовое расстояние кода численно равно:
1) расстоянию между двумя наиболее часто применяемыми кодовыми комбинациями;
2) количеству символов, в которых различаются две наиболее близкие друг к другу комбинации в кодовой таблице;
3) минимальному весу кодовой комбинации;
4) наиболее вероятному значению кратности возникающих ошибок.

31. Кратность ошибок q_o, обнаруживаемых линейным блочным (n,k)-кодом с кодовым расстоянием d_код, подчиняется соотношению:
1) ;
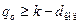2) ;
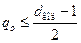3) ;
4) .

32. Кратность ошибок q_и, исправляемых линейным блочным (n,k)-кодом с кодовым расстоянием d_код, подчиняется соотношению:
1) ;
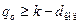2) ;
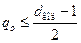3) ;
4) .

33. Простейший код с проверкой на четность способен:
1) обнаруживать любые ошибки нечетной кратности;
2) исправлять любые ошибки нечетной кратности;
3) обнаруживать любые ошибки четной кратности;
4) исправлять любые ошибки четной кратности.

34. Чтобы увеличить корректирующую способность кода, нужно:
1) увеличить количество символов в кодовой комбинации;
2) уменьшить количество избыточных символов;
3) увеличить кодовое расстояние кода;
4) уменьшить кодовое расстояние и увеличить избыточность кода.

35. Число проверок на четность при декодировании комбинации (n,k)-кода равно:
1) n;
2) k;
3) n-k;
4) k-n.

36. При проведении проверок на четность основной операцией является:
1) вычисление остатка от деления чисел;
2) мультиплексирование символов;
3) накопление символов;
4) суммирование символов по модулю 2.

37. Число строк проверочной матрицы (n,k)-кода равно:
1) n-k;
2) k;
3) n;
4) k-n.

38. Число строк производящей матрицы (n,k)-кода равно:
1) n;
2) k;
3) n-k;
4) k-n.

39. Для заданных производящей G и проверочной H матриц (n,k)-кода при подаче на вход строки a информационных символов комбинация на выходе кодера s определяется по формуле:
1) ;
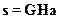2) ;
3) ;
4) .

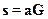40. Для заданных производящей G и проверочной H матриц (n,k)-кода при подаче на вход строки a информационных символов комбинация на выходе кодера sудовлетворяет условию:
1) ;
2) ;
3) ;
4) .

41. Для заданных производящей G и проверочной H матриц (n,k)-кода синдром с для принятой комбинации-строки v определяется по формуле:
1) ;
2) ;
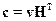3) ;
4) .

42. О наличии ошибок в принятой комбинации-строке v свидетельствует следующее обстоятельство:
1) ;
2) хотя бы один элемент синдрома не равен нулю;
3) синдром оказался записанным в систематической форме;
4) среди элементов синдрома оказались нули.

43. Если при декодировании линейного блочного кода синдром оказался равным нулю, то можно гарантировать, что:
1) в принятой комбинации нет ошибок;
2) такая комбинация есть в кодовой таблице;
3) в принятой комбинации возможно наличие ошибок, но код способен их исправить;
4) принятая комбинация безнадежно искажена помехами.

44. Приведенная таблица может быть:
1) проверочной матрицей линейного блочного кода в систематической форме;
2) производящей матрицей линейного блочного кода в систематической форме;
3) транспонированной проверочной матрицей линейного блочного кода;
4) кодовой таблицей линейного блочного кода.

45. Приведенная таблица может быть:
1) проверочной матрицей линейного блочного кода в систематической форме;
2) производящей матрицей линейного блочного кода в систематической форме;
3) транспонированной проверочной матрицей линейного блочного кода;
4) кодовой таблицей линейного блочного кода.

46. По формуле , где r – количество проверочных символов, определяется:
1) количество информационных символов линейного блочного кода;
2) количество информационных символов систематического кода;
3) избыточность линейного блочного кода;
4) количество символов в комбинации кода Хэмминга.

47. Для кода Хэмминга кодовое расстояние равно:

1) d_код=5

2) d_код=1

3) d_код=4

4) d_код=3

48. Приведенная таблица может быть:
1) проверочной матрицей кода Хэмминга;
2) производящей матрицей линейного блочного кода в систематической форме;
3) производящей матрицей циклического кода;
4) кодовой таблицей линейного блочного кода.

49. Предпочтительным методом кодирования циклического кода является:

1) использование кодовой таблицы;

2) использование многократных проверок на четность;

3) использование проверочной матрицы;

4) использование производящего полинома.

50. Предпочтительным методом декодирования циклического кода является:

1) использование проверочной матрицы;

2) использование производящего полинома;

3) использование кодовой таблицы;

4) использование многократных проверок на четность.

51. По формуле , где r – количество проверочных символов, определяется:
1) количество информационных символов линейного блочного кода;
2) количество информационных символов систематического кода;
3) количество символов в комбинации циклического кода;
4) избыточность линейного блочного кода.

52. Для двоичного линейного блочного (n,k)-кода избыточность R определяется по формуле:
1) ;
2) ;
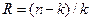3) ;
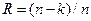4) .

53. В системах с переспросом код, применяемый в прямом канале, используется для:
1) исправления одиночных ошибок и обнаружения остальных;
2) исправления ошибок;
3) обнаружения ошибок;
4) передачи с минимальной избыточностью.

54. Если р – это вероятность появления ошибки в одном символе в канале с независимыми ошибками, то вероятность появления q-кратной ошибки в n-разрядной двоичной комбинации определяется по формуле:
1) ;
2) ;
3) ;
4) .

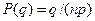55. Если р – это вероятность появления ошибки в одном символе, то среднее количество ошибок в n-разрядной двоичной комбинации определяется по формуле:
1) ;
2) ;
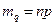3) ;

4) .

56. Для сверточного кода отношение (n-k)/n есть:
1) корректирующая способность кода;
2) коэффициент избыточности;
3) длина кодового ограничения;
4) степень кодирования.

4 кодирование источника

57. Собственная информация, содержащаяся в значении m-ичного символа, имеющего вероятность p_j, равна:
1) ;
2) ;
3) ;
4) .

58. Собственная информация, содержащаяся в значении m-ичного символа, имеющего вероятность p_j, увеличивается при:
1) уменьшении вероятности его появления p_j;
2) увеличении вероятности его появления p_j;
3) уменьшении объема алфавита m;
4) увеличении объема алфавита m.

59. Для оценки величины неопределенности исхода опыта над дискретной случайной величиной используется:
1) энтропия;
2) избыточность;
3) собственная информация;
4) взаимная информация.

60. Для m-ичного символа максимальное значение энтропии H_max равно:
1) ;
2) ;
3) ;
4) .

61. Для последовательности m-ичных символов длиной n ее максимальное значение энтропии H_{n max} равно:
1) ;
2) ;
3) ;
4) .

62. Избыточность в сообщении определяется по формуле:
1) ;
2) ;
3) ;
4) .

63. Избыточность в сообщении определяется по формуле:
1) ;
2) ;
3) ;
4) .

64. Избыточность в сообщении:
1) всегда приносит пользу;
2) всегда приносит вред;
3) иногда нужна для повышения помехоустойчивости;
4) нужна всегда, но в минимальном количестве.

65. Для обеспечения минимальной избыточности в сообщении применяют код:
1) Хафмана;
2) Хэмминга;
3) с одной проверкой на четность;
4) Шеннона-Фано.

66. Средняя длина кодовой комбинации L для безошибочной передачи сообщения X при помощи m-ичных символов должна удовлетворять соотношению:
1) ;
2) ;
3) ;
4) .

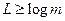67. Причиной появления избыточности в цифровом сигнале является:
1) неравновероятность m значений символа;
2) зависимость символов в передаваемой последовательности;
3) то и другое вместе;
4) наличие повторяющихся отрезков сигнала.

68. При кодировании с минимальной избыточностью для разделения кодовых комбинаций при их последовательной передаче:
1) применяют специальный разделительный символ;
2) в кодовую таблицу включают комбинации одинаковой длины;
3) используют проверку на четность;
4) составляют кодовую таблицу так, чтобы никакая комбинация не являлась началом другой, более длинной.

69. Алфавит удается закодировать последовательностью m-ичных символов с нулевой избыточностью, если:
1) все s букв алфавита равновероятны;
2) s является целочисленной степенью числа m;
3) ероятности всех букв являются отрицательными целочисленными степенями числа m;
4) исходный текст не содержит избыточности, даже если s≠m.

70. Пропускная способность С (бит/символ) m-ичного канала без ошибок равна:
1) ;
2) ;
3) ;
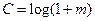4) .

71. Пропускная способность С (бит/символ) двоичного симметричного канала с независимыми ошибками, возникающими с вероятностью р, равна:
1) ;
2) ;
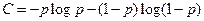3) ;
4) .

72. Пропускная способность С (бит/с) непрерывного канала с ограниченной полосой с белым шумом со спектральной плотностью мощности N_o в зависимости от средней мощности полезного сигнала Р_с определяется по формуле:
1) ;
2) ;
3) ;
4) .