
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Структурный анализ механизмов. Цель и задачи структурного анализа. Определение степени свободы механизма.
Класс и порядок механизма устанавливают по структурной группе, имеющей наиболее высший порядок и класс. Степень свободы пространственного механизма:
W=6n-5P5-4Р4-3Р3-2Р2-Р1 (формула Малышева). Степень подвижности плоского механизма: W=3n-2P5- Р4 (формула Чебышева).
2. Замена механизма на эквивалентную расчетную схему: звено приведения, условия динамической эквивалентности механизма и звена приведения.
С целью упрощения динамических расчётов, реальная схема механизма заменяется динамически-эквивалентной моделью, включающей только одно подвижное звено и стойку, то есть только подвижное звено. Звено приведения – звено, к которому приводятся массы всех подвижных звеньев, силы, действующие на звенья реальных механизмов. Для приведения сил или моментов используется условие динамической эквивалентности: равенство работ или мощностей:  ,
, 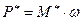 ,
,  ,
, 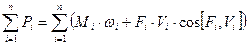 ,
, 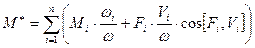 . Приведённый момент (приведённая сила) – условная расчётная величина, которая будучи умноженной на скорость звена приведения, даёт суммарную мощность всех действующих в механизме сил. Приведённая масса (приведённый момент инерции) – это условно расчётная величина, которая, будучи умноженной на половину квадрата скорости, даёт суммарную кинетическую энергию всех подвижных звеньев реального механизма. В качестве условия динамической эквивалентности принимаем равенство кинетических энергий. Кинетическая энергия звена равна суммарной кинетической энергии подвижных звеньев реального механизма.
. Приведённый момент (приведённая сила) – условная расчётная величина, которая будучи умноженной на скорость звена приведения, даёт суммарную мощность всех действующих в механизме сил. Приведённая масса (приведённый момент инерции) – это условно расчётная величина, которая, будучи умноженной на половину квадрата скорости, даёт суммарную кинетическую энергию всех подвижных звеньев реального механизма. В качестве условия динамической эквивалентности принимаем равенство кинетических энергий. Кинетическая энергия звена равна суммарной кинетической энергии подвижных звеньев реального механизма. 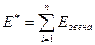 ,
, 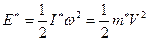 ,
, 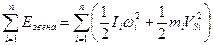 ,
,  .
.
Дата добавления: 2015-04-21; просмотров: 298; Мы поможем в написании вашей работы!; Нарушение авторских прав |