Следствия.

1.

2.

3.

4.

5. для ,

6.

7) Вычисления пределов типа

Lim (log_a (x+1))/x

x->0

lim (ln(x+1))/x

x->0

8) Типа

Lim ((a^x)-1)/x

x->0

Lim ((e^x)-1)/x

x->0

9) Функция непрерывная в точке и непрерывная на интервале

10) Функция, имеющая разрыв первого и второго порядка

11) Теорема Коши о непрерывности функции

12) Теорема Вейрштрассе о непрерывности функции

Функция f(x) непрерывна в точке x = x₀, если для каждого (как угодно малого) ε > 0 существует такое, что .

13) Производная. Ее геометрический и физический смысл

Если функция имеет конечную производную в точке x0, то в окрестности U(x0) её можно приблизить линейной функцией

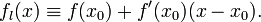
Геометрический смысл производной

Функция fl называется касательной к f в точке x0. Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Физический смысл производной

Скорость изменения функции

Пусть s = s(t) — закон прямолинейного движения. Тогда v(t0) = s'(t0) выражает мгновенную скорость движения в момент времени t0. Вторая производная a(t0) = s''(t0) выражает мгновенное ускорение в момент времени t0.

Вообще производная функции y = f(x) в точке x0 выражает скорость изменения функции в точке x0, то есть скорость протекания процесса, описанного зависимостью y = f(x).

14) Вычисление производной

X^k, e^x, a^x, lnx, log_ax

15) Вычисление производной обратных функций

16) Логарифмическое дифференцирование

17) Дифференциал функции

18) Производная сложной функции

19) Таблица производных

Функция	Производная	Примечание
		Доказательство[показать]
		Доказательство[показать]

20) Теоремы Роля, Коши, Лагранжа о дифференцированных функциях

21) Необходимое и достаточное условие экстремума функции

Необходимое

§ Лемма Ферма. Пусть функция дифференцируема в точке локального экстремума x₀. Тогда:

.

Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.

Достаточное

§ Пусть функция непрерывна в и существуют конечные или бесконечные односторонние производные . Тогда при условии

x₀ является точкой строгого локального максимума. А если

то x₀ является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке x₀

§ Пусть функция f непрерывна и дважды дифференцируема в точке x₀. Тогда при условии

и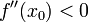

x₀ является точкой локального максимума. А если

и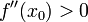

то x₀ является точкой локального минимума.

22) Достаточное условие экстремума по старшей и по второй производной

23) Правило Лапиталя. Неопределенности вида {0/0};{бесконечность/бесконечность}

24) Признаки постоянства, возрастания и убывания функции

25) Достаточное условие выпуклости функции

26) Формула Тейлора для многочлена в степени n

27) Формула Тейлора для произвольной функциию примеры разложения в ряды тейлора следующие функции e^x, sinx, cosx, ln(1+x), (1+x)^n

28) Неопределенный интеграл и его свойства

Неопределённый интегра́л для функции — это совокупность всех первообразных данной функции.

Если функция определена и непрерывна на промежутке и — её первообразная, то есть 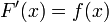при , то

,

где С — произвольная постоянная.

29) Таблица интегралов

30) Замена переменных, как методы интегрирования

31) Интегрирование по частям в неопределенном интеграле типа

Int(ax^2+bx+c)sinx dx, Int(ax^2+bx+c)lnx dx

32) Интегрирование по частям рациональных дробей типа

Int(A/(x-a))dx, int(A/(x-a)^k)dx, int((Ax+B)/(ax^2+bx+c))dx

33) Теорема о разложении рациональной дроби

34) Интегрирование иррациональной функции типа

Int(dx/(ax^2+dx+c)^1/2), Int(dx(Mx+n)/(ax^2+dx+c)^1/2),

35) Интегрирование тригонометрической функции

Int(R(sinxcosx)dx, Int((sinx)^m (cosx)^k)dx

36) Определенный интеграл

37) Свойства определенного интеграла. Теорема о среднем

Теорема о среднем

Пусть функция f (x) непрерывна на [a, b], тогда .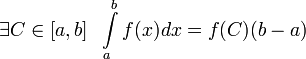

Доказательство

1. По свойству функции, непрерывной на отрезке, , такие что .

2. По свойству определенного интеграла 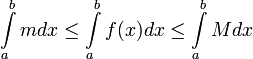, следовательно , 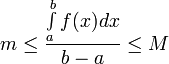. Обозначим дробь как m ^* .

3. Так как непрерывная функция принимает все свои промежуточные значения, а , то , такая что .

38) Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница

Если непрерывна на отрезке 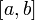и — ее любая первообразная на этом отрезке, то имеет место равенство

39) Замена переменной и интегрирование по частям в определенном интеграле

40) Вычисление длины дуги кривой

41) Вычисление объема тела по площадям параллельных сечений

42) Несобственные интегралы первого и второго рода