Оператор обновления языка SQL

1. Оператор UPDATE

Обновляет существующие записи таблицы БД

UPDATE таблица

SET атр=1значение1[,атр2=знач2,…]

[WHERE условие];

Все записи таблицы, удовлетворяющие условию поиска обновляются в соответствии с присваиванием, указанным за ключевым словом SET

Пример

Установить количество деталей в поставках равным 0 для всех поставщиков из Вашингтона

UPDATE SPJ

SET количество=0

WHERE ‘Вашингтон’ IN

(SELECT город

FROM S

WHERE номер_поставщика=SPJ.номер_пост);

1. Оператор DELETE

DELETE FROM таблица

[WHERE условие];

Из таблицы удаляются все записи, удовлетворяющие условию.

1. Оператор INSERT

В стандарте SQL99 существуют 2 варианта исполнения этого оператора

- Включение одной записи в таблицу (Действует во всех СУБД)

INSERT

INTO таблица [(атр1[,атр2,…])]

VALUES (конст1[,конст2,…]);

В таблицу включается одна запись, имеющая заданные значения для указанных атрибутов, причем i-ая константа соответствует i-му атрибуту. Отсутствие списка атрибутов эквивалентно перечислению всех атрибутов из схемы таблицы

Пример
Добавить в таблицу деталь с номером Р7, цвет и название неизвестны.

INSERT

INTO Р (ном_детали, город,вес)

VALUES (‘P7’,’Лондон’, 0,001);

- Включение нескольких записей в таблицу

INSERT

INTO таблица [(атр1[,атр2,…])]

Подзапрос;

В этом операторе сначала определяется таблица, связанная с подзапросом. Затем строки этой таблицы включаются в исходную таблицу, имя которой указано за ключевым словом INTO. При этом i-ый атрибут подзапроса соответствует i-ому атрибуту в списке атрибутов таблицы.

Пример

Для каждой поставляемой детали найти номер и общее количество и сохранить результат в БД в виду новой таблицы.

CREATE TABLE рабочая

(ном_детали VARCHAR(7);

Общ_кол_в_пост_ NUMBER);

INSERT INTO рабочая

SELECT ном_детали,SUM(количество);

FROM SPJ

GROUP BY ном_детали;

-------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------

БИЛЕТ 25

1. Практические приёмы нормализации схем отношений.

Практические приемы нормализации схем отношения.

1) Приведение схемы отношения к первой нормальной форме.

Схема отношения находится в первой нормальной форме, если она не содержит вектор или других схем отношения.

2) Приведение схемы отношения ко второй нормальной форме.

Схема отношения находится во второй нормальной форме, если не существует ключа Х, множества атрибутов Y 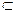X * и не первичного атрибута H Y, для которых были бы справедливы следующие свойства.

· X→Y F⁺

· Y→H F⁺

· Y→X F⁺

(Это определение очень напоминает определение третьей нормальной формы, отличие только в *)

X=A₁A₂

Y=A₁ 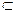X(A₁→A_i…A_j)

H – один из атрибутов A_i…A_j

Так как получилось подобрать X, Y, H è R₁ – не находится во второй нормальной форме.

3) Приведение схемы отношения к третьей нормальной форме.

X=A – ключ.

Y=A₂ 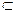R₁(A₂→A_i…A_j)

H=A_i…A_j

Так как подобрали X, Y, H è R₁ ≠ Третьей нормальной форме.

Лекция 12

X=A1A5 – схема отношений R1 (A5 – кат. вектор)

Y=A1(A1→A2A3A4)

H (A2,A3,A4)

A3→A4

Не в 1,2,3 НФ.

Задача нормализовать данную таблицу.

Каждая схема будет в 3НФ, если каждый сотрудник занимает 1 должность на предприятии. Если это не так, то в исходной таблицу R1 входит другая схема, состоящая из других атрибутов.

В этом случае схему БД необходимо преобразовать, т.к. R1 не находится в 1 НФ.

Оптимизации (“на пальцах”)

1. Без потерь – правильные SQL запросы
2. A→B аномалия отсутствие противоречивости, включения
3. потенциальной избыточности.

2. Сравнение синхронной и асинхронной репликации данных.