Выборочный анализ.

Статистический анализ является дальнейшим развитием детерминированного анализа. Спецификой статистического анализа является учет случайных значений факторов и случайных значений результатов. Для исчерпывающего задания случайных значений факторов необходимо определить правило, по которому каждому значению фактора сопоставляется вероятность его появления. Это правило называется Законом распределения вероятностей. Для описания этого закона достаточно задать функцию распределения вероятности.

Для случайной выборки x₁, x₂, … x_n, то по этой выборке можно построить эмпирическую функцию вероятностного распределения Fⁿ(x) и эмпирическую функцию плотности вероятностного распределения .

Vⁿ(x) описывает число случайных значений x_i, величина которых x/

V^k(x) - количество случайных значений в интервале k(x).

k(x) - номер интервала, который включает x.

n - количество значений.

Эмпирическая функция вероятностного распределения Fⁿ(x) в графическом виде называется кумулята, а эмпирическая функция плотности вероятностного распределения - гистограмма.

Вероятностное распределение случайных величин характеризуется следующими основными характеристиками:

1) Математическое ожидание:

для дискретного случая: (p_i - вероятность i-го случая)

для непрерывного случая:

для выборочного ряда:

2) Дисперсия

для дискретного случая: 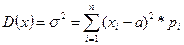( - отклонение значение от среднего)

для непрерывного случая:

для выборочного ряда:

3) момент: начальный и центральный момент

для дискретного случая:

начальный момент -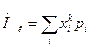

центральный момент -

Полученные характеристики позволяют строить функции плотности вероятностного распределения.

1. Корреляционный анализ.

Наиболее просто характеристикой в степени зависимости двух случайных величин является корреляционный момент. Если случается величина не зависящая друг от друга, то значение корреляционного момента = 0

Вместе с тем корреляционный момент зависит от размерности случайной величины, в одних случаях измерение в тысячах тонн , а в других в долях единицах. Для того чтобы исключить этот недостаток вводят коэффициент корреляции.