Регрессионный анализ.

Основной задачей статистического анализа является определение зависимости средней величины результата от конкретных значений факторов.

y=f(x₁, x₂, … x_n)

Уравнение корреляционной связи y=f(x) уравнением регрессии.

В простейшем случае уравнение регрессии может быть представлено в виде .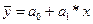

В регрессионном анализе стоит задача - определение коэффициентов а₀ и а₁, которые называются коэффициентами регрессии. Они должны быть такими, чтобы наилучшим образом описывать случайную зависимость. Для этого используют метод наименьших квадратов. Его суть состоит в следующем. Формулируется целевая функция 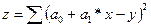→min. Для того чтобы найти минимум целевой функции, необходимо взять производную по параметрам а₀ и а₁ и приравнять эти производные к нулю:

.

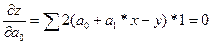
Получаем систему равнений:

n*a₀+a₁*∑x=∑y

a₀∑x+ a₁*∑x²=∑xy

→ min.

Корреляция называется множественной, е средняя величина признака рассматривается в зависимости от нескольких факторов. Если эта зависимость - линейная, то имеется множественное линейное уравнение регрессии, которое имеет следующий вид

.

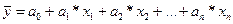Кроме линейного уравнения связи широко используется нелинейное уравнение связи мультипликативного вида

.

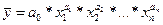Для того чтобы найти коэффициенты регрессии а₀, а₁, а_2, ... , а_n, необходимо исходное кравнение прологарифмировать:

.

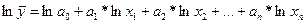Так сводим к линейному 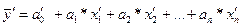и с помощью метода наименьших квадратов определяем все коэффициенты регрессии.