Гидродинамика. В гидродинамике уравнение непрерывности называют уравнением неразрывности

В гидродинамике уравнение непрерывности называют уравнением неразрывности. Оно выражает собой закон сохранения массы в элементарном объеме, то есть непрерывность потока жидкости или газа. Его дифференциальная форма

,

где — плотность жидкости (или газа), — вектор скорости жидкости (или газа) в точке с координатами в момент времени .

Вектор 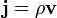называют плотностью потока жидкости. Его направление совпадает с направлением течения жидкости, а абсолютная величина определяет количество вещества, протекающего в единицу времени через единицу площади, расположенную перпендикулярно вектору скорости.

Для несжимаемых жидкостей . Поэтому уравнение принимает вид

,

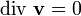из чего следует соленоидальность поля скорости.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

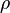— плотность жидкости,

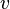— скорость потока,

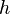— высота, на которой находится рассматриваемый элемент жидкости,

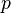— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

— ускорение свободного падения.

В научной литературе закон Бернулли, как правило, называется уравнением Бернулли^[1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли^[2][3] или интегралом Бернулли^[4][5].

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»^[6]).

Соотношение, близкое^[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы и уравнение Бернулли принимает вид: .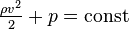

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности : .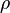

Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового , статического и динамического давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.