
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Б) Относительно обработки
| Значение критерия "Уровень потерь" | Стоимость восстановления | ||
| Незначительная | Средняя | Большая | |
| Незначительный | 1о | 2о | Зо |
| Средний | 4о | 5о | 6о |
| Большой | 7о | 8о | 9о |
Таким образом, оказалось, что при выбранных значениях составляющих критериев вся информация делится на семнадцать классов важности. Однако номер класса сам по себе не характеризует важность информации на содержательном уровне, да и оперировать семнадцатью различными классами затруднительно. С целью преодоления указанных трудностей, разделим все элементы классификационной структуры так, как показано в табл. 7.2 пунктирными линиями. В итоге семнадцать классов разделились на семь категорий важности, которым присвоим следующие содержательные наименования:
МлВ - маловажная (категория А);
Об В - обыкновенной важности (категория Б);
Пс В - полусредней важности (категория В);
Ср В- средней важности {категория Г);
Пв В - повышенной важности (категория Д);
Бл В - большой важности (категория Е);
ЧрВ- чрезвычайной важности (категория Ж).
Таблица 7.2- Итоговая классификация информации по важности
| Важность информации | Относительно обработки | |||||||||
| 1о | 2о | 3о | 4о | 5о | 6о | 7о | 8о | 9о | ||
| Относительно назначения | 1н |     1 1
| ||||||||
| 2н | ||||||||||
| 3н |  5 5
| |||||||||
| 4н | ||||||||||
| 5н | ||||||||||
| 6н |  11 11
| |||||||||
| 7н | ||||||||||
| 8н | ||||||||||
| 9н |
С такими житейски понятными категориями оперировать гораздо проще, однако для проведения аналитических расчетов необходимо иметь количественное выражение показателей важности. Для обеспечения этих возможностей поступим следующим образом. Естественно предположить, что важность информации категории А убывает от класса 3 к классу 1, приближаясь к 0, а категории Ж возрастает от класса 15 к классу 17, приближаясь к 1. Естественно также предположить, что возрастание важности информации от класса 1 к классу 17 происходит неравномерно; наиболее адекватной, видимо, будет зависимость в виде логистической кривой. Графически это можно представить так, как показано на рис. 7.2.
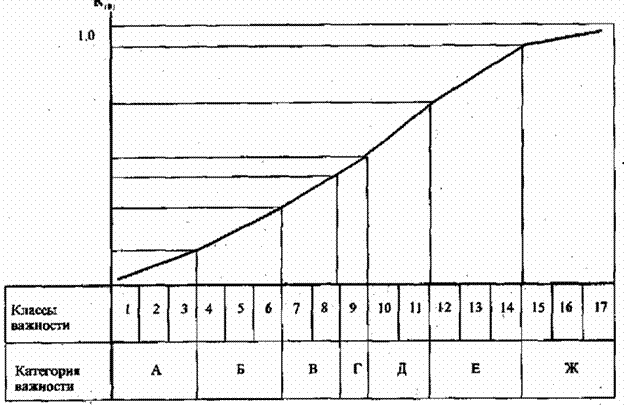
Рисунок 7.2- Графиккоэффициента важностиинформации
Нетрудно видеть, чтотеперь мы имеем все необходимое для строго алгоритмического определения показателя важности информации, причем как в качественном, так и в количественном выражениях. Последовательность и содержание такой оценки приведены на рис. 7.3.

Рисунок 7.3.Последовательность и содержание оценки важности информации.
12. Оценка полноты информации
Полнота есть показатель, характеризующий меру достаточности информации для решения соответствующих задач.Отсюда следует, что данный показатель, так же как и предыдущий является относительным: полнота информации оценивается относительно вполне определенной задачи или группы задач. Поэтому, чтобы иметь возможность определять показатель полноты информации, необходимо для каждой задачи или группы задач заблаговременно составить перечень сведении, которые необходимы для их решения. Для представления таких сведений удобно воспользоваться так называемыми объектно-характеристическими таблицами (ОХТ), каждая из которых есть двухмерная матрица, по строкам которой приведен перечень наименовании объектов, процессов или явлений, которые входят в круг интересов соответствующей задачи, а по столбцам - наименования их характеристик (параметров), значения которых необходимы для решения задачи. Сами значения характеристик будут располагаться на пересечении соответствующих строк и столбцов. Совокупность всех ОХТ, необходимых для обеспечения решения всех задач предприятия (учреждения, другой организации), может быть названа информационным кадастром объекта. Таким образом, непременным условием оценки полноты информации является наличие информационного кадастра.
Методика оценки полноты может быть следующей.
Обозначим через  элемент, находящийся в
элемент, находящийся в  -и строке и v-м столбце рассматриваемого компонента соответствующей ОХТ, причем:
-и строке и v-м столбце рассматриваемого компонента соответствующей ОХТ, причем:

Тогда в качестве меры коэффициента полноты информации в данной ОХТ можно принять величину:
 , (7.4)
, (7.4)
где т - число строк,
п - число столбцов в рассматриваемой ОХТ.
Однако при этом не учитывается важность, значимость различных элементов, причем важность в том смысле, как это рассматривалось выше. Пусть
 есть коэффициент важности элемента
есть коэффициент важности элемента  -й строки и v-гo столбца.
-й строки и v-гo столбца.
Тогда, очевидно, в качестве меры взвешенной полноты информации в рассматриваемой ОХТ можно принять величину:
 (7.5)
(7.5)
13. Оценка релевантность информации
Релевантность есть такой показатель информации, который характеризует соответствие ее потребностям решаемой задачи. Для количественного выражения данного показателя обычно используют так называемый коэффициент релевантности K(р) определяющий отношение объема релевантной информации Np к общему объему анализируемой информации N0:
K(р) =  (7.6)
(7.6)
Сущность коэффициента релевантности очевидна, но трудности практическое его использования сопряжены количественным выражением объема информации. В сфере научно-технической информации под N0, например, понимается общее количество документов, выданных назапрос, а под Np - количество релевантных среди общего объема.
К оценке релевантности фактографической информации можно подойти следующим образом. Пусть имеется информационный кадастр, состоящий из некоторого количества ОХТ. Тогда релевантность  -й ОХТ можно выразить формулой:
-й ОХТ можно выразить формулой:
 , (7.7)
, (7.7)
где

или с учетом коэффициентов важности элементов ОХТ:
 (7.8)
(7.8)
Коэффициент релевантности всего информационного кадастра, очевидно, может быть выражен формулой:
 (7.9)
(7.9)
или с учетом коэффициентов важности элементов ОХТ:
 (7.10)
(7.10)
14. Оценка адекватности информации
Под адекватностью информации понимается степень ее соответствия действительному состоянию тех реалий, которые отображает оцениваемая информация. В общем случае адекватность определяется двумя параметрами: объективностью генерирования информации о предмете, процессе или явлении и продолжительностью интервала времени между моментом генерирования информации и текущим моментом, т.е. до момента оценивания ее адекватности.
Объективность генерирования информации, очевидно, зависит от способа получения значений характеристик предмета, процесса или явления и качества реализации способа в процессе получения этих значений.
Классификация характеристик по возможным способам получения их значений приведена на рис. 8.1 Тогда все возможные значения адекватности информации по объективности ее генерирования можно структурировать так, как приведено в табл. 8.1.

Рисунок. 8.1 - Классификация характеристик по способам получения их значений
Таблица 8.1 - Структуризация значений адекватности информации по объективности генерирования

Как и при разработке методики оценки важности информации сделаем естественное предположение, что при хорошем качестве определения значения непосредственно и притом количественно измеряемой характеристики адекватность соответствующей информации будет близка к 1, а при плохом определении значения неизмеряемой характеристики, не имеющей даже отдаленного аналога, адекватность информации близка к нулю. Естественно также предположить, что внутри данного интервала изменение адекватности происходит по логистической кривой, как это показано на рис. 8.2.
Рассмотрим теперь адекватность информации по второму названном выше параметру - продолжительности интервала времени между моментом генерирования информации и текущим моментом. Для оценки адекватности по данному параметру вполне подходящим является известный в теории информации так называемый закон старения информации. Его вид показан на рис. 8.3. При этом под t0 понимается момент времени генерирования оцениваемой информации. Как следует из рисунка, закон старения информации характеризуется четырьмя характерными интервалами:
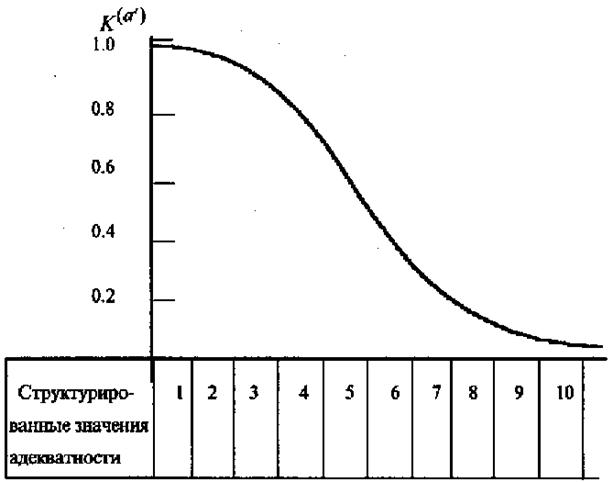
Рисунок 8.2 - График зависимости показателя адекватности информации по способу генерирования
∆t1 -продолжительность интервала времени, в течение которого оцениваемая информация полностью сохраняет свою адекватность;
∆t2 -продолжительность интервала времени, втечение которого адекватность информации падает, но не более, чем на одну четверть;
∆t3 - продолжительность интервала времени, в течение которого адекватность информации падает наполовину;
∆t4 - продолжительность интервала времени, в течение которого адекватность информации падает на три четверти;
Учитывая то обстоятельство, что обе составляющие адекватности информации K(  ) и K
) и K  зависят от большого числа факторов, многие из которых носят случайный характер, есть основания утверждать, что они в основе своей также имеют случайный характер и поэтому могут интерпретироваться как вероятности того, что информация по соответствующему параметру является адекватной. Поскольку для подавляющего большинства теоретических интересов и практических приложений важно, чтобы информация была адекватна по обоим параметрам, то в соответствии с теоремой умножения вероятностей общий показатель адекватности информации К(а) может быть определен как:
зависят от большого числа факторов, многие из которых носят случайный характер, есть основания утверждать, что они в основе своей также имеют случайный характер и поэтому могут интерпретироваться как вероятности того, что информация по соответствующему параметру является адекватной. Поскольку для подавляющего большинства теоретических интересов и практических приложений важно, чтобы информация была адекватна по обоим параметрам, то в соответствии с теоремой умножения вероятностей общий показатель адекватности информации К(а) может быть определен как:
К(а) = K(  )K
)K  (8.1)
(8.1)

Рисунок 8.3 - Общий вид закона старения информации
Независимость величин K(  ) и K
) и K  представляется вполне естественной.
представляется вполне естественной.
15. Оценка толерантности, эффективности кодирования и объема информации
Толерантность, как отмечалось выше, есть показатель, характеризующий удобство восприятия и использования информации в процессе решения задачи. Уже из самого определения видно, что понятие толерантности является очень широким, в значительной мере неопределенным и субъективный. Даже для цифровой информации значение толерантности может быть самым различным. Поэтому вряд ли можно надеяться на разработку строго формальной методики определения толерантности. Из эвристических методов наиболее подходящими здесь представляются неформально-эвристические и особенно - методы экпертно-лингвистических оценок. При этом в качестве значений лингвистической переменной могут быть такие:
1) весьма удобно, комфортно - когда информация представлена в таком виде, что ее использование в процессе решения задачи происходит естественным образом, не требуя дополнительных усилий;
2) удобно- когда использование информации если и требует дополнительных усилий, то лишь незначительных;
3) средне - когда использование информации требует дополнительных усилий, вообще говоря, допустимых;
4) плохо - когда использование информации сопряжено с большими трудностями;
5) очень плохо - когда использование информации или вообще невозможно, или требует неоправданно больших усилий.
Показатели второго вида. Как определено выше, основными показателями второго вида являются эффективность кодирования и объем информации. Поскольку методы определения названных показателей достаточно полно разработаны в теории информации, то специально на них останавливаться нет необходимости.
Требуемый уровень защиты информации должен определяться с учетом значений всех рассмотренных выше показателей. Методика такого определения может базироваться на следующей полуэвристической процедуре:
1) все показатели информации делятся на три категории: определяющие, существенные и второстепенные, причем основным критерием для такого деления должна служить та цель, для достижения которой осуществляется защита информации в соответствующей АСОД;
2) требуемый уровень защиты определяется по значениям определяющих показателей информации;
3) выбранный уровень при необходимости может быть скорректирован с учетом значения существенных показателей. Значения второстепенных показателей при этом могут игнорироваться.
Возможный вариант классификации показателей информации в зависимости от целей защиты приведен в табл. 8.2.
Таблица 8.2 - Классификация значений показателей информации в зависимости от целей защиты.
| Показатель информации | Вид сохраняемой тайн | Защита информации как товара | ||
| Военной, государственной, научной | Промышленной, коммерческой | Конфиденциальной | ||
| Важность | Определяющее | Определяющее | Определяющее | Определяющее |
| Полнота | Существенное | Существенное | Определяющее | Определяющее |
| Адекватность | Существенное | Существенное | Существенное | Определяющее |
| Релевантность | Второстепенное | Существенное | Существенное | Существенное |
| Толерантность | Второстепенное | Второстепенное | Второстепенное | Существенное |
| Способ кодирования | Второстепенное | Второстепенное | Второстепенное | Существенное |
| Объем | Второстепенное | Существенное | Существенное | Определяющее |
16. Общая структура программы формирования перечня факторов, влияющих на требуемый уровень защиты информации
Естественно, что требуемый уровень зашиты информации в конкретной АСОД и в конкретных условиях ее функционирования существенно зависит от учета факторов, которые сколько-нибудь существенно влияют да защиту. Таким образом, формирование возможно более полного множества этих факторов и возможно более адекватное определение степени их влияния на требуемый уровень защиты представляется задачей повышенной важности и подлежащей упреждающему решению.
Сформулированная задача, однако, практически не поддается решению традиционными формальными методами. Если бы в наличии были статистические данные о функционировании систем и механизмов защиты информации в различных АСОД(различных по функциональному назначению, архитектуре, характеру обрабатываемой информации, территориальному расположению, технологии обработки информации, организации работы и т.п.), то, вообще говоря, данную задачу можно было бы решить статистической обработкой этих данных, по крайней мере, по некоторому полуэвристическому алгоритму. Но такие данные в настоящее время отсутствуют, и их получение в обозримом будущем представляется весьма проблематичным. В силу сказанного в настоящее время для указанных целей можно воспользоваться лишь неформально-эвристическими методами, т.е, с широким привлечением знаний, опыта и интуиции компетентных и заинтересованных специалистов.
Нетрудно видеть, что задача довольно четко может быть разделена на две составляющие: формирование возможно более полного и хорошо структурированного множества факторов, существенно значимых с точки зрения защиты информации, и определение показателей значимости (веса) факторов. В классе неформально-эвристических методов выделены методы экспертных оценок, мозгового штурма и психо-интеллектуальной генерации. Анализируя содержание выделенных составляющих задач и существо названных неформально-эвристических методов, нетрудно заключить, что для решения первой из них наиболее эффективным представляется метод психо-интеллектуальной генерации, а второй - методы экспертных оценок.Что касается метода мозгового штурма, то он может быть использован для решения обеих составляющих задач, особенно для обсуждения ранее полученных решении.
Основным реквизитом метода психо-интеллектуальной генерации выступает так называемая психо-эвристическая программа (ПЭП), представляющая собой перечень и последовательность (общий алгоритм) обсуждения вопросов, составляющих существо решаемой задачи, развернутую схему обсуждения каждого вопроса, а также методические указания, обеспечивающие целенаправленное обсуждение каждого из выделенных в общем алгоритме вопросов.
17. Схема вопросов обсуждения перечня групп факторов, влияющих на защиту информации
При разработке ПЭП для обоснования множества факторов, влияющих на требуемый уровень защиты информации, следует исходить из того, что этих факторов, вообще говоря, большое количество, и они носят разноплановый характер. Поэтому представляется целесообразным разделить их на некоторое число групп, каждая из которых объединяла бы факторы какого-либо одного плана. Тогда задачу формирования возможно более полного множества факторов можно решать по трехшаговой процедуре: первый шаг - формирование перечня групп факторов, второй - формирование перечня факторов в каждой из выделенных групп, третий - структуризация возможных значений двух факторов. Общая схема ПЭП для решения рассматриваемой задачи по такой процедуре представлена на рис. 9.1.
Развернутые схемы обсуждения выделенных на общей схеме вопросов рассмотрим на примере первого и второго вопросов, имея в виду, что по остальным вопросам подобные схемы могут разрабатываться студентами в порядке самостоятельной работы.
Вопрос 1 - первоначальное формирование перечня групп факторов. Решение данного вопроса может осуществляться двояко: перечень групп факторов предварительно сформированили такой перечень отсутствует. В первом случае обсуждение должно вестись в целях обоснования содержания и возможной корректировки перечня, во втором - формирования перечня и затем уже его обоснования и уточнения.

Рисунок 9.1 - Общая структура программы формирования перечня факторов, влияющих на требуемый уровень защиты информации
На рис. 9.2 приведена развернутая схема обсуждения применительно к первому случаю.

Рисунок 9.2 - Схема вопросов обсуждения перечня групп факторов, влияющих на защиту информации
18. Пример страницы психо-эвристической программы
Методическое обеспечение лучше всего представить в виде структурированной страницы, составляемой для каждого вопроса развернутой схемы и содержащей четыре элемента: вопросник, напоминатель, указатель и решатель. На рис. 9.3 приведена такая страница применительно к вопросу 1 показанной на рис. 9.2 схемы вопросов.
Для других вопросов такие страницы могут быть разработаны студентами в порядке самостоятельной работы.

Рисунок 9.3 - Пример страницы ПЭП
Сформированное по указанной методологии множество факторов включает пять групп следующего содержания.
Группа 1 - обуславливаемые характером обрабатываемой информации:
1.1. Степень секретности.
1.2. Объемы.
1.3. Интенсивность обработки.
Группа 2 - обуславливаемые архитектурой АСОД:
2.1. Геометрические размеры.
2.2. Территориальная распределенность.
2.3. Структурированность компонентов.
Группа 3 - обуславливаемые условиями функционирования АСОД:
3.1. Расположение в населенном пункте.
3.2. Расположение на территории объекта.
3.3. Обустроенность.
Группа 4 - обуславливаемые технологией обработки информации:
4.1. Масштаб.
4.2. Стабильность.
4.3. Доступность.
4.4. Структурированность,
Группа 5 - обуславливаемые организацией работы АСОД;
5.1. Общая постановка дела.
5.2. Укомплектованность кадрами.
5.3. Уровень подготовки и воспитания кадров.
5.4. Уровень дисциплины.
Значение всех факторов выражены в лингвистических переменных и приведены в табл. 9.1.
Таблица 9.1- Значения факторов, влияющих на требуемый уровень защиты информации
| Наименование группы факторов | Наименование факторов | Значение факторов |
| Обуславливаемые характером обрабатываемой информации | 1.1. Степень секретности | Очень высокая Высокая Средняя 4.Невысокая |
| 1.2. Объемы | Очень большие Большие Средние 4. Малые | |
| 1.3.Интенсивность обработки | Очень высокая Высокая Средняя 4. Низкая | |
| Обуславливаемые архитектурой АСОД | 2.1.Геометрические размеры | 1 . Очень большие Большие Средние 4 Незначительные |
| 2.2. Территориальная распределенность | Очень большая Большая Средняя 4. Незначительная | |
| 2.3. Структурированность компонентов | Полностью отсутствует Частичная Достаточно высокая 4.Полная | |
| 3.Обусловливаемые условиями функционирования АСОД | 3. 1 . Расположение в населенном пункте | Очень неудобное Создает значительные трудности для защиты 3. Создает определенные трудности для защиты 4. Очень хорошее |
| 3.2. Расположение на территории объекта | 1 . Хаотично разбросанное Разбросанное Распределенное 4. Компактное | |
| З.З. Обустроенность | Очень плохая Плохая Средняя 4. Хорошая | |
| 4.Обуславливаемые технологии обработки информации | 4.1. Масштаб | 1 . Очень большой 2. Большой Средней 4. Незначительный |
| 4.2. Стабильность | 1.Отсутствует 2. Частично стабильная Достаточно упорядоченная 4. Регулярней | |
| 4.3. Доступность | Общедоступная С незначительными ограничениями на доступ С существенными ограничениями на доступ 4. С полным регулируемым доступом | |
| 4.4. Структурированность | Полностью отсутствует Частичная Достаточно высокая 4. Полная | |
| 5.Обуславливаемые организацией работы АСОД | 5.1. Общая постановка дела | Очень плохая Плохая Средняя 4. Хорошая |
| 5.2. Укомплектованность кадрами | 1 . Очень слабая 2. Слабая Средняя 4. Полная | |
| 5.3. Уровень подготовки и воспитания кадров | Очень низкий Низкий Средней 4. Высокий | |
| 5.4. Уровень дисциплины | Очень низкий Низкий Средний 4. Высокий |
Нетрудно видеть, что значения всех факторов сведены в некоторую унифицированную схему и расположены они так, что на первом месте находятся значения, предопределяющие наиболее высокие требования к защите информации, а на пятом - наиболее низкие требования.
Таким образом, всего выделено 17 факторов, каждый из которых может принимать одно из четырех значений. Следовательно, общее число различных вариантов потенциально возможных условий защиты выразится весьма внушительной величиной, а именно - количеством возможных сочетаний из 17  4 =68 элементов по 17. Как известно, количество различных сочетаний из n элементов по
4 =68 элементов по 17. Как известно, количество различных сочетаний из n элементов по  определяется по формуле:
определяется по формуле:
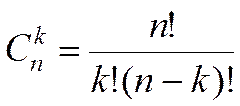
Подставляя в эту формулу наши значения n и k,получаем:
 т. е. число астрономического порядка.
т. е. число астрономического порядка.
В общем случае для каждого из потенциально возможных вариантов условий должны быть определены свои требования к защите информации, что при таком количестве вариантов практически невозможно. Следовательно, необходимо разделить все множество возможных вариантов на некоторое (сравнительно небольшое) число классов, в рамках каждого из которых все входящие в него варианты должны считаться идентичными с точки зрения требований к защите информации. Как следует из проведенных выше вычислений, указанная классификация сопряжена с решением комбинаторной задачи весьма большой размерности и с высоким уровнем неопределенности.
19. Значение факторов, влияющих на требуемый уровень защиты информации
При обосновании постановки задачи определения требований к защите информации было показано, что конечная цель анализа факторов, влияющих на требуемый уровень защиты информации, заключается в делении всего множества вариантов потенциально возможных условий защиты на некоторое (желательно как можно меньшее) число классов, каждый из которых будет объединять варианты, близкие по показателям требуемой защиты. Важность такой классификации очевидна: системы защиты, удовлетворяющие требованиям выделенных классов условий, могут быть представлены типовыми, что создаст объективные предпосылки для эффективного решения проблемы защиты информации на регулярной основе в массовом масштабе. Для практической реализации такой классификации необходим показатель, количественно характеризующий относительные важности вариантов условий с точки зрения требований к защите.
На сформированной ранее классификационной структуре факторов выделено три уровня: группа факторов, факторы в пределах группы, значения факторов. Тогда, если обозначить:
 - весi-й группы факторов в общем перечне групп;
- весi-й группы факторов в общем перечне групп;
 – вес j-го фактора в i-й группе;
– вес j-го фактора в i-й группе;
 - вес k-го значения j-го фактора в i-й группе,
- вес k-го значения j-го фактора в i-й группе,
то вес m-го варианта условий защиты  , очевидно, выразится функцией:
, очевидно, выразится функцией:
 (10.1)
(10.1)
Отсюда следует, что решение сформулированной задачи сводится к определению величин Ri, Qij, Sijk и вида функциональной зависимости (10.1).
Мы уже знаем, что для определения значений перечисленных выше величин целесообразнее всего использовать методы экспертных оценок. Анализ сущности рассматриваемых величин позволяет утверждать, что для их определения могут быть использованы практически все изученные в предыдущем семестре разновидности экспертных оценок. Рассмотрим методику использования некоторых из них.
20. Определение весов вариантов потенциально возможных условий защиты информации
В качестве примера рассмотрим определение весов групп факторов с использованием количественной бальной оценки при формировании оценки по методу парных сравнений. Как это было констатировано ранее, названная разновидность экспертных оценок заключается в том, что каждый из экспертов оценивает объекты, события, параметры путем присвоения каждой паре из них коэффициента превосходства одной над другой. При этом, естественно, предполагается, что если  есть коэффициент превосходства объекта А над объектом В, то
есть коэффициент превосходства объекта А над объектом В, то  - коэффициент превосходства объекта В над объектом А - выражается величиной
- коэффициент превосходства объекта В над объектом А - выражается величиной  .
.
На рисунке 10.1 приведена заполненная экспертом соответствующая анкета, причем справа от таблицы приведены возможные значения коэффициентов предпочтения и их смысловое содержание, а в табл. 10.1 - сводные данные об оценках групп факторов коллективом из 21 эксперта. Обработка приведенных результатов по изученной ранее методике дает значения, показанные в крайней справа колонке табл. 10.1.
Экспертная оценка важности групп факторов, определяющих требования к защите информации
Значения относительной важности
| Группа факторов | № групп факторов | 
| |||||
| № | Наименование | ||||||
| Характер обрабатываемой информации | |||||||
| Архитектура СОД | 
| 
| |||||
| Условия функционирования СОД | 
| 
| 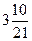
| ||||
| Технология обработки информации | 
| 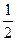
| 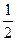
| 
| |||
| Организация работы СОД | 
| 
| 
| 
|
Шкала относительной важности
1 - равная важность
3 - умеренное превосходство одной над другой
5 - существенное превосходство
7 - значительное превосходство
9 - очень сильное превосходство 2, 4, 6, 8 - промежуточные значения
Эксперт Белов
Рисунок 10.1 - Анкета экспертизы по методу парных сравнений
Таблица 10.1 - Сводные данные экспертной оценке важности групп факторов группой на 21 эксперта
| №№ группы факторов | Эксперт | 
| |||||||||||||||||||||
| 10,3 | 1,1 | 0,6 | 15,33 | ||||||||||||||||||||
| 9,2 | 7,5 | 8,1 | 5,6 | 15,5 | 15,5 | 15,5 | 1,4 | 1,2 | 7,4 | 3,6 | 2,3 | 0,8 | 2,5 | 1,3 | 2,2 | 7,7 | 0,9 | 8,05 | |||||
| 3,5 | 1,9 | 3,5 | 3,6 | 3,3 | 3,3 | 3,3 | 2,9 | 8,5 | 0,8 | 9,7 | 2,3 | 5,4 | 1,5 | 3,2 | 3,8 | 3,9 | 1,2 | 3,59 | |||||
| 4,2 | 2,2 | 5,3 | 5,8 | 5,8 | 5,8 | 3,7 | 0,8 | 2,3 | 8,7 | 8,5 | 7,7 | 8,7 | 7,11 | ||||||||||
| 1,2 | 2,7 | 2,5 | 3,5 | 3,8 | 3,8 | 3,8 | 8,3 | 8,3 | 7,5 | 8,73 | |||||||||||||
Рассмотрим далее вопрос о виде функциональной зависимости (10.1), т.е. веса варианта условий  в зависимости от величин
в зависимости от величин  ,
,  ,
,  .
.
Наиболее простой и в то же время часто используемой функцией в подобных ситуациях является произведение составных коэффициентов при условии, что они нормированы по одной шкале. Поскольку величины  ,
,  ,
,  нормированы по шкале 0-1, то тогда
нормированы по шкале 0-1, то тогда
 (10.2)
(10.2)
а чтобы и величины  были нормированы в той же шкале, можно воспользоваться зависимостью:
были нормированы в той же шкале, можно воспользоваться зависимостью:
 (10.3)
(10.3)
Однако ранее было показано, что общее количество потенциально возможных вариантов условий защиты выражается числом астрономического порядка, и осуществить вычисления по этой зависимости практически невозможно.
21. Теоретический подход к решению задачи формирования необходимого и достаточного набора типовых систем защиты информации
Теоретический подход.Задачи деления элементов множества на классы изучаются уже продолжительное время, и для их решения в классической теории систем разработан достаточно представительный арсенал различных методов. Наиболее общим из этих методов является так называемый кластерный анализ, который определяется как классификация объектов по осмысленным, т.е. соответствующим четко сформулированным целям группам. Основная суть кластерного анализа заключается в том, что элементы множества делятся на классы в соответствии с некоторой мерой сходства между различными элементами.
Процедура кластеризации в общем виде может быть представлена последовательностью пяти шагов следующего содержания:
1) формирование множества элементов, подлежащих делению на классы;
2) определение множества признаков, по которым должны оцениваться элементы множества;
3) определение меры сходства между элементами множества;
4) деление элементов множества на классы;
5) проверка соответствия полученного решения поставленным цепям.
Нетрудно видеть, что применительно к рассматриваемой здесь задаче первые два шага сделаны на предыдущих занятиях. Рассмотрим возможныеподходы к осуществлению следующих шагов приведенной процедуры.
Третий шаг, как это сформулировано выше, заключается в определении меры сходства между элементами классифицируемого множества. Нет необходимости доказывать, что выбором меры сходства элементов в решающей степени определяется результат классификации, его соответствие поставленным целям, поэтому данный шаг считается центральным.
В теоретическом плане решение этой задачи заключается в формировании соответствующей метрики, т.е. представление элементов множества точками некоторого координатного пространства, в котором различие и сходство элементов определяется метрическим расстоянием между соответствующими элементами. Любая метрика должна удовлетворять совокупности следующих условий:
1) симметричности:

где x и у - различные элементы множества,
 - расстояние между элементами хи у;
- расстояние между элементами хи у;
2) неравенства треугольника:
 ,
,
где x, y, z - различные элементы множества;
3) различимости неидентичных элементов:
 где х, у - идентичные элементы;
где х, у - идентичные элементы;
4) неразличимости идентичных элементов:
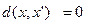 , где xи x’- идентичные элементы.
, где xи x’- идентичные элементы.
Нетрудно показать, что показатель важности варианта условий  отвечает всем приведенным выше условиям метрики.
отвечает всем приведенным выше условиям метрики.
Что касается самого значения меры сходства, то наибольшее распространение получили следующие три: коэффициент корреляции, расстояние и коэффициент ассоциативности.
Коэффициент корреляции между элементами с номерами j и  вычисляется по следующей зависимости:
вычисляется по следующей зависимости:
 , (11.1)
, (11.1)
где  и
и  - значения i-йпеременной для элементов j и k соответственно,
- значения i-йпеременной для элементов j и k соответственно,  и
и  - среднее всех значений соответствующих элементов, n - число элементов.
- среднее всех значений соответствующих элементов, n - число элементов.
Под расстоянием dij как мерой сходства понимается величина
 , (11.2)
, (11.2)
или
 , (11.3)
, (11.3)
где  и
и  - значения i-й переменной для i-го и j-гоэлементов соответственно, р - число переменных в оценке элементов.
- значения i-й переменной для i-го и j-гоэлементов соответственно, р - число переменных в оценке элементов.
Коэффициент ассоциативности (S) используется для оценки меры сходства элементов, описываемых бинарными переменными. Вычисляется он по зависимости:
 , (11.4)
, (11.4)
причем значения входящих в нее величин берутся из матрицы:


где 1 означает наличие соответствующей переменной, а 0 - ее отсутствие.
Нетрудно видеть, что при d=0 выражение для коэффициента ассоциативности имеет вид:
 . (11.5)
. (11.5)
Основная задача кластерного анализа заключается в рациональном делении анализируемого множества элементов на кластеры (классы) в соответствии с выбранной мерой сходства. Основными характеристиками, по которым оцениваются выделенные кластеры считаются: плотность, дисперсия, размеры, форма и отделимость.
22. Эмпирический подход к решению задачи формирования необходимого и достаточного набора типовых систем защиты информации
Плотность характеризует уровень скопления (количество, близость) элементов, классифицируемых в классе, дисперсия - степень рассеивания элементов в координатном пространстве относительно центра кластера, размеры - "радиус" кластера, форма - геометрию расположения элементов в кластере, отделимость - степень перекрытия кластеров и расстояние между ними в координатном пространстве.
К настоящему времени разработано большое количество различных методов деления множества элементов на кластеры. Все эти методы могут быть разделены на следующие группы:
1) иерархические агломеративные,
2) иерархические дивизивные,
3) итеративные группировки,
4) поиска модальных значений плотности,
5) факторные,
6) сгущений,
7) основанные на теории графов.
Наибольшее распространение в практических приложениях получили иерархические агломеративные методы. Их суть в общем виде заключается в представлении классифицируемых элементов в виде древовидной структуры (дендрограммы) в зависимости от степени взаимосвязей между ними. Общий вид дендрограммы приведен на рисунке 11.4.

Рисунок 11.4 - Дендрограммы кластерного анализа по иерархическому алгомеративному методу
Деление дендрограммы на кластеры осуществляется различными методами, причем наибольшее распространение получили следующие четыре: одиночной связи, полной связи, средней связи и так называемый метод Уорда.
По методу одиночной связикластер образуется по правилу: элемент включается в уже сформированный кластер, если хотя бы один из элементов кластера находится на том же уровне, что и анализируемый.
Метод полной связипредполагает, что анализируемый элемент включается в существующий кластер, если его сходство с каждым элементом кластера не превосходит задаваемого порога.
Метод средней связизаключается в вычислении среднего сходства анализируемого элемента со всеми элементами в уже существующем кластере. Элемент включается в кластер, если значение среднего сходства не превосходит устанавливаемого порога.
Метод Уордапостроен таким образом, чтобы оптимизировать минимальную дисперсию в пределах создаваемых кластеров. Целевая функция определяется как сумма квадратов отклонений и вычисляется по формуле:
 (11.11)
(11.11)
где Xj- значение для j-го элемента характеристики, по которой осуществляется кластеризация. В кластеры включаются элементы, которые дают минимальное приращение СКО.
Нетрудно показать, что полученные ранее оценки факторов, влияющих на требуемый уровень защиты информации, позволяют сформировать меру близости между различными вариантами условий, удовлетворяющую рассмотренным выше требованиям. Наиболее простым выражением данной меры близости вариантов т'и т" будет:
 . (11.12)
. (11.12)
Нетрудно построить и другие приведенные выше меры, сделать это можно самостоятельно.
Практическая реализация строго теоретического подхода к решению рассматриваемой задачи наталкивается на так называемое "проклятие размерности", заключающееся в непреодолимых вычислительных трудностях ввиду того, что множество потенциально возможных вариантов условий защиты характеризуется, как это было показано, числом астрономического порядка. Возможные пути преодоления указанных трудностей будут рассмотрены ниже при изложении сущности теоретико-эмпирического подхода.
Эмпирический подход. Сущность данного подхода, как это следует из самого его названия, заключается в решении рассматриваемой задачи на основе опыта и здравого смысла компетентных специалистов. К настоящему времени известно несколько примеров выделения типовых систем защиты информации. Так, нетрудно видеть, что рассмотренные ранее наиболее известные методы выделения типовых СЭИ основаны преимущественно на эмпирическом подходе, примем без какого-либо объективного обоснования.
Но при наличии рассмотренных ранее весов возможных вариантов защиты (притом нормированных в интервале 0-1) можно предложить более наглядный, и потому психологически более приемлемый метод, основанный на эвристическом подходе.
Смысл веса варианта заключается в том, что чем больше этот вес, тем выше требования к защите информации в соответствующих условиях. Тогда требования кзащите в зависимости от весов вариантов можно представить так, как показано на рисунок 11.5 (выделенные интервалы получены методом половинного деления). Требования к защите будут определяться тем из выделенных на рисунок 11.5 интервалов, в который попадает соответствующее значение Wm. Возможные характеристики выделенных СЗИ приведены в табл. 11.3.
 |
Рисунок 11.5 - Определение требований к защите информации методом половинного деления шкалы 0-1
Таблица 11.3. Характеристики типовых СЗИ по уровню зашиты информации
| № п/п | Класс СЗИ по уровню защиты | Ориентировочное количественное значение уровня защиты | Общая характеристика СЗИ |
| Слабой защиты |  0,5 0,5
| Обеспечивается защита в пределах возможностей серийных средств обработки информации и общедоступных организационно-правовых мер | |
| Средней защиты | 0,5-0,75 | Может быть достигнута путем пополнения серийных средств общедоступных организационных мер некоторыми средствами регулирования и разграничения доступа и поддержанием достаточно четкого уровня организации обработки информации | |
| Сильной защиты | 0,75-0,87 | Может быть обеспечена комплексным применением широкого спектра различных средств защиты и строгой организацией процессов функционирования СОД | |
| Очень сильной защиты | 0,87 -0,93 | Может быть обеспечена при соблюдении трех условий: наличие развитой и высоко организованной СЗИ; Строжайшая организация процессов жизнедеятельности СОД; 3) непрерывное управление процессами защиты | |
| Особой защиты | >0,93 | Дополнительно к 'предыдущему требуется: создание СЗИ по индивидуальному проекту; 2) реализация мандатной системы доступа |
Ранее было введено понятие стратегии защиты как общей направленности усилий по защите информации, причем выделено три стратегии: оборонительная, наступательная и упреждающая. Естественно предположить, что каждый из выделенных выше уровней защиты может достигаться в рамках каждой из предусмотренных стратегий. Исключениями из этого правила могут быть только следующие ситуации: в рамках оборонительной стратегии вряд ли целесообразно предусматривать очередь сильную (и тем более - особую) защиту, а особая защита даже в рамках наступательной стратегии может рассматриваться скорее в виде исключения; аналогично можно предположить, что слабая защита (не предусматривающая использование дополнительных средств защиты) не может носить наступательный (а тем более - упреждающий) характер; сомнительно также, чтобы средняя защита носила упреждающий характер.
Тогда общая классификационная структура СЗИ может быть представлена так, как показано на рисунок 11.6, причем прямоугольниками обведены и обозначены цифрами без индексов основные классы систем, a об ведены пунктиром и обозначены цифрами с индексами - дополнительные.
Конкретное содержание механизмов защиты типовых СЗИ может быть определено на основе анализа характеристик факторов, влияющих на требуемый уровень защиты. Фрагменты таких характеристик в содержательном выражении приведены в таблица 11.4.
Рассмотрим еще один метод, основанный на эмпирической подходе. Вычислим значения:
 , (11.13)
, (11.13)
 . (11.14)
. (11.14)
В целях нормализации значению Wm(i,j,k)(max) припишем вес, равный 1, a Wm(i,j,k)(min) - 0. Соответственно для варианта с Wm(max) вероятность надежной защиты должна быть близка к 1, а для варианта с Wm(min) - близка к 0. Для определения промежуточных значений выбирается функция:
 (11.15)
(11.15)
наиболее адекватно отражающая существо процессов защиты информации вне временных системах ее обработки.
Здесь  - требуемая вероятность надежной защиты, a
- требуемая вероятность надежной защиты, a  -приведенное по норме 0-1 значение Wm. Очевидно:
-приведенное по норме 0-1 значение Wm. Очевидно:
| Уровень защиты | Стратегия защиты | |||||
| Оборонительная | Наступательная | Упреждающая | ||||
| Слабый |
| |||||
| Средний |
|  

| ||||
| Сильный |
|
|
| |||
| Очень сильный | 
|
|
| |||
| Особый | 
|
|
Рисунок 11.6 -Классификационная структуратиповых СЗИ
Таблица 11.4. Характеристики факторов, влияющих не требуемый уровень защиты информации
| Наименование группы факторов | Наименование факторов | Значения факторов | Условия присвоений значений факторов | Требования к: ищите информации |
| Обусловливаемые обрабатываемой информацией | Степень секретности информации | Очень высокая | Нарушение защищенности информации ведет к крупномасштаб- ным невосполнимым потерям | 1 . Доступ к информации по мандатам ограничения действия 2.Исключение с вероятностью, близкой к 1, косвенной утечки информации по техническим каналам 3. То же по организационным каналам |
| Высокая | Нарушение защищенности ведет к достаточно крупным и трудновосполнимым потерям | Высокоэффективное разграничение доступа к информации при опознавании пользователи с вероятностно, близкой к 1 Надежная (с вероятностью не ниже 0,93) защита от утечки информации по техническим каналам каналам 3. То же по организационным каналам | ||
| Средняя | Нарушение защищенности может привести к весьма ощутимым потерям, восполнение которых может потребовать значительных усилий и расходов | Разграничение доступа к информации с использованием сертифицированных серийных средств Предупреждение косвенной утечки информации с использованием недорогих серийных средств 3. Организация обработки информации с соблюдением общепринятых правил обработки защищаемой информации | ||
| Низкая | Нарушение защищенности не ведет к ощутимым потерям | Дополнительные средства защиты не требуются |

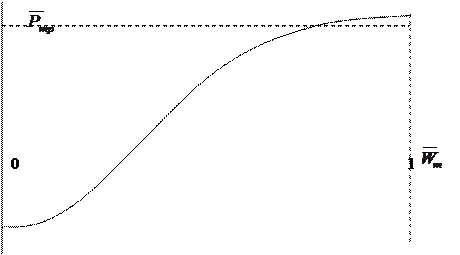
В качестве функции f(  ) целесообразнее всего принять так называемую логистическую кривую, вид которой приведем на рис. 11.7.
) целесообразнее всего принять так называемую логистическую кривую, вид которой приведем на рис. 11.7.
 | |||
 |
Рисунок 11.7 - Вид функции 
23. Теоретико-эмпирический подход к решению задачи формирования необходимого и достаточного набора типовых систем защиты информации
Теоретико-эмпирический подход. Как следует из самого названия, данный подход основывается на комплексном использовании рассмотренных выше теоретического и эмпирического подходов. При этом естественным представляется стремление в максимальной степени использовать результаты строгого анализа задачи и определить те трудности, которые при этой возникают.
Дезагрегируем общую классификационную структуру факторов, влияющих на требуемый уровень защиты, на части: первую, включающую факторы первой и второй групп, вторую, включающую факторы третьей, четвертой и пятой групп, но только с учетом первых двух значений каждого фактора, и третью, тоже включающую факторы третьей, четвертой и пятой групп, но с учетом последних двух значений каждого фактора. Проведем затем классификацию вариантов условий в пределах каждой выделенной части (например, по рассмотренному выше иерархи вескому алгомеративному методу), а затем на основе полученных три дендрограмм составим общую, на основе которой и выделим типовые классы вариантов условий.
Общее число вариант
Дата добавления: 2015-04-18; просмотров: 506; Мы поможем в написании вашей работы!; Нарушение авторских прав |