
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Схема действующих сил к выводу основного уравнения гидростатики
 (1)
(1)
Уравнение (1) называют основным уравнением гидростатики.
Механические процессы, классификация.
Механические процессы, скорость которых определяется законами физики твердого тела.

|
Расчет диаметра трубопроводов и аппаратов
При проектных расчетах длина трубопроводов обычно задана, основной задачей является определение диаметра трубопровода, а также расхода энергии на транспортирование.
При известном расходе жидкости Q диаметр трубопровода может быть определен по уравнению расхода  . Отсюда диаметр трубопровода
. Отсюда диаметр трубопровода  при средней скорости жидкости
при средней скорости жидкости 
 .
.
Таким образом, единственной переменной, от которой зависит диаметр трубопровода, является скорость w протекания жидкости по трубопроводу. С увеличением скорости диаметр трубопровода уменьшается и, следовательно, снижается его стоимость за счет снижения затрат на изготовление трубопровода, его монтаж и ремонт. Но при этом увеличиваются потери напора и соответственно затраты энергии на транспортирование жидкости. Очевидно, что наиболее рациональный – оптимальный – диаметр трубопровода, учитывающий противоречивое влияние скорости на величину общих годовых затрат З, может быть выбран на основе технико-экономического расчета. Для этого строят графическую зависимость общих годовых затрат З от диаметра трубопровода  (рис. 3). Минимум на кривой соответствует такому диаметру трубопровода, при котором скорость транспортирования жидкости оптимальна.
(рис. 3). Минимум на кривой соответствует такому диаметру трубопровода, при котором скорость транспортирования жидкости оптимальна.

| ||||
| Рис. 3.6. Изменение затрат при увеличении диаметра трубопровода: З – общие годовые затрат; А – затраты на амортизацию и ремонт; Э – эксплуатационные расходы |
При расчете диаметра химических аппаратов используют аналогичный подход. Как и при расчете трубопроводов определяют диаметр аппарата и гидравлическое сопротивление. Однако выбор скорости w потока в химических аппаратах усложняется рядом обстоятельств, специфичных для каждой группы аппаратов. Поскольку скорость потока существенно влияет на тепло- и массоперенос, выбор скорости потока в аппарате должен быть тесно связан с расчетом процесса, осуществляемого в том или ином аппарате.
Для ориентировочных расчетов диаметра трубопроводов (а также штуцеров и других деталей и узлов химических аппаратов) можно использовать опытные данные по скоростям движения жидкостей и газов в промышленных условиях, приведенные ниже:
| Среда и условия движения | Скорость, м/с |
| маловязкие жидкости (до 0,01 Па/с) при перекачивании насосом . . . . . . . . . . . . . . . . . . . | . . . . . . 0,5–3,0; |
| вязкие жидкости (свыше 0,01 Па/с) при перекачивании насосом . . . . . . . . . . . . . . . . . . . | . . . . . . 0,2–1,0; |
| жидкости при движении самотеком . . . . . . | . . . . . . 0,1–0,5; |
| газы при низком давлении (до 10 кПа) . . . . | . . . . . . . 8–15; |
| то же, при повышенном давлении . . . . . . . . | . . . . . . .15–25; |
| пар насыщенный . . . . . . . . . . . . . . . . . . . . . . | . . . . . . .15–25; |
| то же, перегретый . . . . . . . . . . . . . . . . . . . . . | . . . . . . .20–50. |
Теоретические методы исследования химико-технологических процессов
Теория подобия и анализ размерностей представляют собой основные направления обобщенного анализа – учения о методах универсализации количественного исследования, т. е. определения наиболее рациональной формы представления получаемых результатов, которой соответствует максимально возможная степень расширения области их применимости.
Практическая ценность результата количественного исследования обусловлена, с одной стороны, полнотой и конкретностью содержащейся в нем информации, а с другой – широтой области его применимости. Полнота знаний о конкретном процессе достигается в том случае, когда учтено влияние всех существенных для него факторов. Чтобы отразить это влияние, приходится вводить в задачу соответствующее число параметров.
Параметрами называются величины, характеризующие индивидуальные особенности конкретного процесса. Каждому процессу свойственны определенные значения этих величин, которые изменяются при переходе от одного частного случая к другому. Наряду с независимыми переменными параметры являются аргументами задачи.
Очевидно, каждый параметр в определенном отношении сужает область применимости полученного результата. Таким образом, требования, определяющие ценность результатов исследования, в известном смысле оказываются взаимно противоречащими. Это противоречие может быть заметно ослаблено, если использовать рациональную форму представления результатов, получаемую на основе методов обобщенного анализа.
Фундаментальная идея обобщенного анализа заключается
в замещении множества отдельных аргументов – параметров – совокупностью безразмерных комплексов, число которых, как правило, меньше общего числа первоначальных размерных
параметров. Тем самым повышается степень общности результата без потери содержащейся в нем информации. Термины «теория подобия» и «анализ размерностей» отражают скорее особенности используемых технических средств, чем принципиальную сущность методов обобщенного анализа.
Теория подобия – метод, основанный на анализе замкнутой системы математических уравнений, описывающих рассматриваемое явление. Использование анализа размерностей позволяет определить структуру безразмерных комплексов, если соответственно типу задачи выбрана система единиц, а также составлен перечень величин, существенных для рассматриваемого процесса.
В современной литературе встречается несколько вариантов терминологии в области теории подобия и анализа размерностей. В данной работе будут использоваться термины, рекомендованные «Комиссией по терминологии в области теории теплообмена».
Исследование принимает количественную форму, когда характеристиками процесса становятся величины, представленные числами. Существуют две различные операции приведения характеристик процесса к числу.
В первом случае сопряжение величины с числом происходит в результате прямого измерения, т. е. сопоставления ее с образцом произвольно выбранного, но строго фиксированного размера. Этот принимаемый в качестве стандарта образец называется основной единицей измерения, а сама физическая величина – первичной величиной.
Если  – число, выражающее соотношение между измеряемой величиной
– число, выражающее соотношение между измеряемой величиной  и стандартом
и стандартом 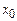 , то
, то  . Очевидно, что
. Очевидно, что  зависит от выбора единицы измерения и изменяется обратно пропорционально ее размеру. В отличие от этого отношение чисел, соответствующих различным образцам величины
зависит от выбора единицы измерения и изменяется обратно пропорционально ее размеру. В отличие от этого отношение чисел, соответствующих различным образцам величины  , не зависит от выбора единицы. Это характерное свойство операции прямого измерения коротко определяется как абсолютность отношений.
, не зависит от выбора единицы. Это характерное свойство операции прямого измерения коротко определяется как абсолютность отношений.
Например, когда высота цилиндра и его диаметр рассматриваются порознь, они могут принимать различные значения в зависимости от выбора единицы длины. Но их отношение всегда оказывается одним и тем же, выражая объективное свойство данного геометрического тела, не зависящее ни от процедуры измерения, ни от выбора единицы длины.
Наряду с первичными, вводятся вторичные величины, численные значения которых получаются на основе определительных уравнений (тождеств), устанавливающих связь между численными значениями рассматриваемой вторичной величины и соответствующих первичных.
Определительное уравнение выражается через степенной одночлен вида
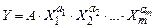 ,
,
где 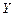 и
и 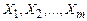 – численные значения вторичной и первичных величин соответственно;
– численные значения вторичной и первичных величин соответственно;  – произвольная постоянная. Производная единица вторичной величины устанавливается соответственно соглашению об обращении этой величины в единицу, когда все первичные величины приравнены единице (условие
– произвольная постоянная. Производная единица вторичной величины устанавливается соответственно соглашению об обращении этой величины в единицу, когда все первичные величины приравнены единице (условие  ).
).
Эффективность применения обобщенного анализа в значительной степени зависит от способа решения задачи и используемых при этом средств. Известны три основных средства количественного анализа: аналитическое решение задачи, эксперимент, численное решение.
Если аналитическое решение задачи получено в общем виде, то не составляет труда вычислить значения искомых характеристик процесса для любого момента времени в любой точке пространства. Кроме того, можно проследить влияние каждого фактора, установить связь любых величин, существенных для процесса. Применение методов обобщенного анализа в этом случае не дает каких-либо заметных преимуществ, хотя и позволяет представить решение в более компактной форме. Однако из-за большой сложности задач и высоких требований к точности их решения возможности получить аналитическое решение сильно ограничены. Довести его до конца удается очень редко, и покупается это ценой значительных упрощений задачи. Поэтому в настоящее время аналитическое исследование задачи (особенно для технических приложений) практически является лишь принципиальной возможностью.
Основное значение приобретают численные методы исследования: непосредственный (или модельный) эксперимент и решение задач с помощью ЭВМ. Объем информации, получаемой при численном решении задачи на ЭВМ, обычно во много раз больше, чем при экспериментальном исследовании ее. Кроме того, экспериментальное определение характеристик требует значительных материальных затрат и существенно большего времени. Однако в отличие и от аналитического исследования, и от численного решения на ЭВМ возможность применения экспериментального метода не зависит от наличия математического описания изучаемого явления. Именно эта особенность и делает опыт критерием оценки не только качества решения задачи, но и правильности ее постановки. Таким образом, каждый из этих двух методов численного исследования имеет достоинства, которыми не обладает другой. Поэтому при решении достаточно сложных задач используются оба этих метода одновременно.
И в том, и в другом случае результаты исследования представляют собой числовые массивы. Разница заключается лишь в их объеме и в том, как они были получены: в результате вычислений или измерений. Массивы содержат большой объем полезной информации, однако их использование связано со значительными трудностями. В первую очередь это обусловлено тем, что при численном способе исследования параметры оказываются своего рода переменными, поскольку каждому варианту численного расчета (или каждому отдельному опыту) соответствует их конкретное значение. Если обозначить общее число независимых переменных (координаты, время) и параметров через  и условно принять, что для определения влияния каждого из этих аргументов достаточно десяти вариантов его значений, то общее количество значений искомой переменной будет равно
и условно принять, что для определения влияния каждого из этих аргументов достаточно десяти вариантов его значений, то общее количество значений искомой переменной будет равно  . Большинство современных задач являются многопараметрическими, поэтому для получения достаточно полного представления о влиянии всех аргументов задачи требуются громадные затраты машинного времени (громадный объем экспериментальной работы). Кроме того, возникает проблема упорядочивания и хранения полученной информации. Иногда оказывается более рациональным заново решать задачу по известной программе, чем хранить результаты предыдущих расчетов. Разумеется, это приемлемо лишь для конкретных расчетных задач и ни в коей мере не допустимо для научных исследований, в которых основную роль играет познавательная ценность получаемых результатов.
. Большинство современных задач являются многопараметрическими, поэтому для получения достаточно полного представления о влиянии всех аргументов задачи требуются громадные затраты машинного времени (громадный объем экспериментальной работы). Кроме того, возникает проблема упорядочивания и хранения полученной информации. Иногда оказывается более рациональным заново решать задачу по известной программе, чем хранить результаты предыдущих расчетов. Разумеется, это приемлемо лишь для конкретных расчетных задач и ни в коей мере не допустимо для научных исследований, в которых основную роль играет познавательная ценность получаемых результатов.
В таких условиях использование обобщенного анализа создает принципиальные преимущества, поскольку уменьшение числа аргументов задачи при переходе к безразмерным комплексам на одну или несколько единиц на столько же порядков снижает число значений искомой переменной. Для расчетных задач при этом в соответствующее число раз уменьшаются затраты машинного времени, а для экспериментальных – число необходимых опытов. Для научных же исследований, помимо этого, весьма важно, что при использовании обобщенного анализа повышается познавательная ценность результатов.
Анализ численных результатов непосредственно в том виде, в котором они получаются, дает возможность установить конкретные соотношения, характеризующие рассматриваемую задачу. Однако такого рода эмпирические корреляции имеют ограниченное применение и не могут дать сколько-нибудь отчетливой физической картины изучаемого явления, поскольку не определяют его общих закономерностей. В противоположность этому использование обобщенного анализа непосредственно приводит к установлению количественных закономерностей процесса. Уже сама математическая структура безразмерных комплексов создает основу для суждения взаимных связях отдельных факторов, характере эффектов, обусловленных их совместным влиянием.
Классификация насосов. Основные параметры насосов
Дата добавления: 2015-04-21; просмотров: 245; Мы поможем в написании вашей работы!; Нарушение авторских прав |